第5课 分式
知识点:
分式，分式的基本性质，最简分式，分式的运算，零指数，负整数，整数，整数指数幂的运算
大纲要求:
了解分式的概念，会确定使分式有意义的分式中字母的取值范围。掌握分式的基本性质，会约分，通分。会进行简单的分式的加减乘除乘方的运算。掌握指数指数幂的运算。
考查重点与常见题型:
1．考查整数指数幂的运算，零运算，有关习题经常出现在选择题中，如：下列运算正确的是（ ）
（A）-40 =1 (B) (-2)-1= (C) (-3m-n)2=9m-n (D)(a+b)-1=a-1+b-1
2.考查分式的化简求值。在中考题中，经常出现分式的计算就或化简求值，有关习题多为中档的解答题。注意解答有关习题时，要按照试题的要求，先化简后求值，化简要认真仔细，如：
化简并求值：
. +(–2),其中x=cos30°,y=sin90°
知识要点
1．分式的有关概念
设A、B表示两个整式．如果B中含有字母，式子
就叫做分式．注意分母B的值不能为零，否则分式没有意义
分子与分母没有公因式的分式叫做最简分式．如果分子分母有公因式，要进行约分化简
2、分式的基本性质
（M为不等于零的整式）
3．分式的运算
(分式的运算法则与分数的运算法则类似)．
(异分母相加，先通分)；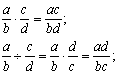
4．零指数 
5．负整数指数 
注意正整数幂的运算性质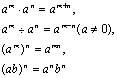 
可以推广到整数指数幂，也就是上述等式中的m、 n可以是O或负整数．
考查题型:
1． 下列运算正确的是（ ）
（A）－40 =1 (B) (－2)-1= (C) (－3m-n)2=9m-n (D)(a+b)-1=a-1+b-1
2．化简并求值：
. +(–2),其中x=cos30°,y=sin90°
3．、、、、、ａ＋ｂ、 中分式有＿＿＿
4．当x=-----------时， 分式的值为零；
5．当x取---------------值时，分式有意义；
6．已知＝＋是恒等式，则A＝＿＿＿，B＝＿＿＿。
7．化简(– )÷
8．先化简后再求值：÷+,其中x=
9．已知＝2，求的值
考点训练：
1，分式 当x=----------- 时有意义，当x=-----------时值为正。
2，分式中的取值范围是（ ）
（A）x≠1 （B）x≠-1 （C）x≠0 （D）x≠±1且x≠0
3，当x=-------------------时，分式的值为零？
4，化简
（1）1－+ (2) • ÷
(3) [a+(a-)• ]÷(a-2)(a+1)
(4)。已知b(b－1)－a(2b－a)=－b+6，求–ab的值
＊(5).[(1+)(x－4+)–3]÷ (–1)
＊(6). 已知x+=，求 的值
＊（7）若ａ＋ｂ＝1，求证：－＝
解题指导,
1．当a=----- -时,分式无意义,当a-=----- -时,这个分式的值为零.
2．写出下列各式中未知的分子或分母,
(1) = (2)=
3．不改变分式的值,把分式的分子,分母各项的系数化为整数,且最高次项的系数均为正整数,得-------------------------，分式约分的结果为＿＿＿＿。
4．把分式中的x,y都扩大两倍,那么分式的值( )
(A)扩大两倍 (B) 不变 (C) 缩小 (D) 缩小两倍
5．分式－, , 的最简公分母为( )
(A) 4(m－n)(n－m)x2 (B) (C)4x2(m－n)2 (D)4(m－n)x2
6．下列各式的变号中,正确的是
(A)= － ( B)= (C) =(D)＝－
7．若x >y>0,则－ 的结果是( )
(A) 0 (B)正数 (C) 负数 (D) 以上情况都有可能
8．化简下列各式:
(1) +－ (2) (xy+y2)÷ ·
＊(3) [1－(a－)2÷ ]·
(4) 若(–1)a=1，求 －+1的值
(5) 已知 x2－5xy+6y2=0 求 的值
独立训练
1．化简÷ ·
＊2．当a=时，求分式(－ +1) ÷的值
＊3．化简 4。已知 += 值,求+的值
5．已知m2－5m+1=o 求(1) m3+ (2)m－的值
＊6。当x=1998,y=1999时， 求分式 的值
7．已知==,求 的值
＊ 8．化简
＊（9）＝求的值。
＊（10）设＋＋＝，求证：ａ、ｂ、ｃ三个数中必有两个数之和为零。