中考数学动态型试题
动态几何问题是近几年各地中考试题常见的压轴试题,它能考查学生的多种能力,有较强的选拔功能。
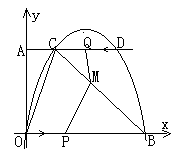
例1在三角形![]() 中,
中, ![]() .
.
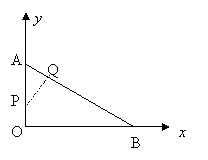
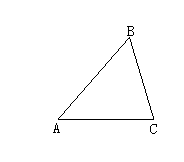 现有动点
现有动点![]() 从点
从点![]() 出发, 沿射线
出发, 沿射线![]() 向点
向点![]() 方向运动; 动点
方向运动; 动点![]() 从点
从点![]() 出发, 沿射线
出发, 沿射线![]() 也向点
也向点![]() 方向运动. 如果点
方向运动. 如果点![]() 的速度是
的速度是![]() /秒, 点
/秒, 点![]() 的速度是
的速度是![]() /秒, 它们同时出发, 求:(1)几秒钟以后,
/秒, 它们同时出发, 求:(1)几秒钟以后, ![]() 的面积是
的面积是![]() 的面积的一半?
的面积的一半?
(2)这时, ![]() 两点之间的距离是多少?
两点之间的距离是多少?
分析:本题是动态几何知识问题,此类题型一般利用几何关系关系式列出方程求解。
解:(1) 设![]() 秒后,
秒后, ![]() 的面积是
的面积是![]() 的面积的一半,
的面积的一半,
则![]() , 根据题意, 列出方程
, 根据题意, 列出方程
|
|
![]() ,
,
化简, 得![]() ,
,
解得![]() . 所以2秒和12秒均符合题意;
. 所以2秒和12秒均符合题意;
(2) 当![]() 时,
时, ![]()
在![]() 中,作
中,作![]() 于
于![]() ,
,
在![]() 和
和![]() 中,
中, ![]() ,
,
所以![]() ;
;
当![]() 时,
时, ![]() 同理可求得
同理可求得![]() .
.
说明:本题考查了用一元二次方程、三角函数等有关知识进行几何图形的面积计算方法。
练习一
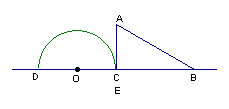
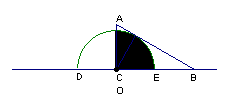
1、如图,形如量角器的半圆O的直径DE=12cm,形如三角板的⊿ABC中,∠ACB=90°,∠ABC=30°,BC=12cm。半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上。设运动时间为t (s),当t=0s时,半圆O在⊿ABC的左侧,OC=8cm。
(1)当t为何值时,⊿ABC的一边所在直线与半圆O所在的圆相切?
(2)当⊿ABC的一边所在直线与半圆O所在的圆相切时,如果半圆O与直线DE围成的区域与⊿ABC三边围成的区域有重叠部分,求重叠部分的面积。
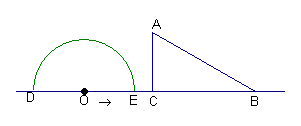
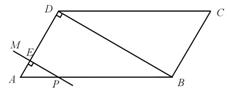
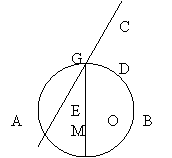
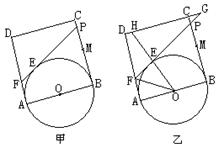
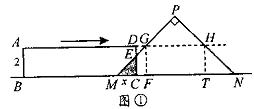
2、已知,如图(甲),正方形ABCD的边长为2,点M是BC的中点,P是线段MC上的一个动点, P不运动到M和C,以AB为直径做⊙O,过点P作⊙O的切线交AD于点F,切点为E.
(1)求四边形CDFP的周长;
(2)试探索P在线段MC上运动时,求AF·BP的值;
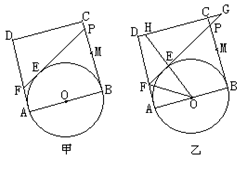 (3)延长DC、FP相交于点G,连结OE并延长交直线DC于H(如图乙),是否存在点P,
(3)延长DC、FP相交于点G,连结OE并延长交直线DC于H(如图乙),是否存在点P,
使△EFO∽△EHG?如果存在,试求此时的BP的长;如果不存在,请说明理由。
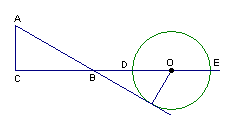
3、如图,AB是⊙O的直径,点C是BA延长线上一点,CD切⊙O于D点,弦DE∥CB,Q是AB上一动点,CA=1,CD是⊙O半径的![]() 倍。
倍。
(1)求⊙O的半径R。
(2)当Q从A向B运动的过程中,图中阴影部分的面积是否发生变化,若发生变化,请你说明理由;若不发生变化,请你求出阴影部分的面积。
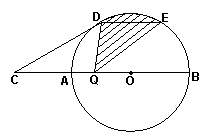 |
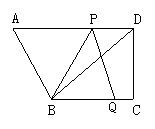
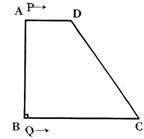
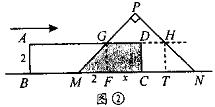
4、如图,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=16,DC=12,AD=21。动点P从点D出发,沿射线DA的方向以每秒2两个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P,Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动。设运动的时间为t(秒)。
(1)设△BPQ的面积为S,求S与t之间的函数关系式;
(2)当t为何值时,以B,P,Q三点为顶点的三角形是等腰三角形?
(3)当线段PQ与线段AB相交于点O,且2AO=OB时,求∠BQP的正切值;
(4)是否存在时刻t,使得PQ⊥BD?若存在,求出t的值;若不存在,请说明理由。
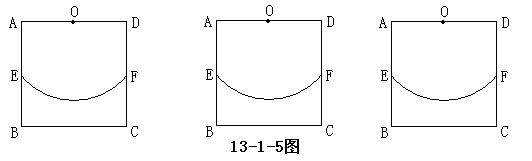
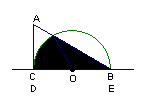
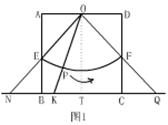
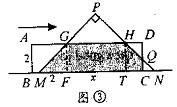
5、如图,在边长为2个单位长度的正方形ABCD中,点O、E分别是AD、AB的中点,点F是以点O为圆心、OE的长为半径的圆弧与DC的交点,点P是![]() 上的动点,连结OP,并延长交直线BC于点
上的动点,连结OP,并延长交直线BC于点![]() .
.
(1)当点P从点E沿![]() 运动到点F时,点
运动到点F时,点![]() 运动了多少个单位长度?
运动了多少个单位长度?
(2)过点P作![]() 所在圆的切线,当该切线不与BC平行时,设它与射线AB、直线BC分别
所在圆的切线,当该切线不与BC平行时,设它与射线AB、直线BC分别
交于点M、G.
①当K与B重合时,BG∶BM的值是多少?
②在点P运动的过程中,是否存在BG∶BM=3的情况?你若认为存在,请求出BK的值;你若认为不存在,试说明其中的理由.
一般地,是否存在BG∶BM=n(n为正整数)的情况?试提出你的猜想(不要求证明).
| |
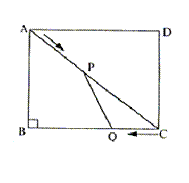 例2如图,在矩形ABCD中,AB=6米,BC=8米,动点P以2米/秒的速度从点A出发,沿AC向点C移动,同时动点Q以1米/秒的速度从点C出发,沿CB向点B移动,设P、Q两点移动t秒(0<t<5)后,四边形ABQP的面积为S米2。
例2如图,在矩形ABCD中,AB=6米,BC=8米,动点P以2米/秒的速度从点A出发,沿AC向点C移动,同时动点Q以1米/秒的速度从点C出发,沿CB向点B移动,设P、Q两点移动t秒(0<t<5)后,四边形ABQP的面积为S米2。
(1)求面积S与时间t的关系式;
(2)在P、Q两点移动的过程中,四边形ABQP与△CPQ的面积能否相等?若能,求出此时点P的位置;若不能,请说明理由。
分析:本题是一个动态几何问题,也是一个数形结合的典型问题,综合性较强。
解:(1)过点P作(1) 设![]() 秒后,
秒后, ![]() 的面积是
的面积是![]() 的面积的一半,
的面积的一半,
则![]() , 根据题意, 列出方程
, 根据题意, 列出方程
![]() ,
,
化简, 得![]() ,
,
解得![]() . 所以2秒和12秒均符合题意;
. 所以2秒和12秒均符合题意;
(2) 当![]() 时,
时, ![]() 在
在![]() 中, 作
中, 作![]() 于
于![]() ,
,
在![]() 和
和![]() 中,
中, ![]() ,
,
所以![]() ;
;
当![]() 时,
时, ![]() 同理可求得
同理可求得![]() .
.
说明:本题考查的知识点较多,考查了勾股定理、平行线分线段成比例定理,一元二次方程及一元二次方程及根的判别式。
练习二
1、)如图,已知直角梯形ABCD中,AD∥BC,ÐB=90º,AB=12cm,BC=8cm,DC=13cm,动点P沿A→D→C线路以2cm/秒的速度向C运动,动点Q沿B→C线路以1cm/秒的速度向C运动。P、Q两点分别从A、B同时出发,当其中一点到达C点时,另一点也随之停止。设运动时间为t秒,△PQB的面积为ym2。
(1)求AD的长及t的取值范围;
(2)当1.5≤t≤t0(t0为(1)中t的最大值)时,求y关于t的函数关系式;
(3)请具体描述:在动点P、Q的运动过程中,△PQB的面积随着t的变化而变化的规律。
2、如图,在Rt△ABC中,已知AB=BC=CA=4cm,AD⊥BC于D,点P、Q分别从B、C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s;点P沿CA、AB向终点B运动,速度为2cm/s,设它们运动的时间为x(s)。
⑴求x为何值时,PQ⊥AC;
⑵设△PQD的面积为y(cm2),当0<x<2时,求y与x的函数关系式;
⑶当0<x<2时,求证:AD平分△PQD的面积;
⑷探索以PQ为直径的圆与AC的位置关系。请写出相应位置关系的x的取值范围(不要求写出过程)

3、如图,在平行四边形ABCD中,AD=4 cm,∠A=60°,BD⊥AD. 一动点P从A出发,以每秒1 cm的速度沿A→B→C的路线匀速运动,过点P作直线PM,使PM⊥AD .
(1) 当点P运动2秒时,设直线PM与AD相交于点E,求△APE的面积;
(2) 当点P运动2秒时,另一动点Q也从A出发沿A→B→C的路线运动,且在AB上以每秒1 cm的速度匀速运动,在BC上以每秒2 cm的速度匀速运动. 过Q作直线QN,使QN∥PM. 设点Q运动的时间为t秒(0≤t≤10),直线PM与QN截平行四边形ABCD所得图形的面积为S cm2 .
 ① 求S关于t的函数关系式;
① 求S关于t的函数关系式;
② (附加题) 求S的最大值.
4、已知:如图,△ABC中,∠C=90°,AC=3厘米,CB=4厘米.两个动点P、Q分别从A、C两点同时按顺时针方向沿△ABC的边运动.当点Q运动到点A时,P、Q两点运动即停止.点P、Q的运动速度分别为1厘米/秒、2厘米/秒,设点P运动时间为![]() (秒).
(秒).
(1)当时间![]() 为何值时,以P、C、Q三点为顶点的三角形的面积(图中的阴影部分)等于2厘米2;
为何值时,以P、C、Q三点为顶点的三角形的面积(图中的阴影部分)等于2厘米2;
(2)当点P、Q运动时,阴影部分的形状随之变化.设PQ与△ABC围成阴影部分面积为S(厘米2),求出S与时间![]() 的函数关系式,并指出自变量
的函数关系式,并指出自变量![]() 的取值范围;
的取值范围;
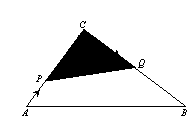 (3)点P、Q在运动的过程中,阴影部分面积S有最大值吗?若有,请求出最大值;若没有,请说明理由.
(3)点P、Q在运动的过程中,阴影部分面积S有最大值吗?若有,请求出最大值;若没有,请说明理由.
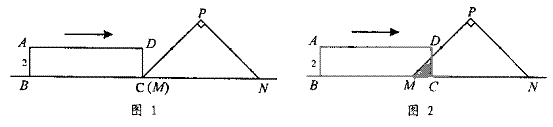 5、如图1,Rt△PMN中,∠P=90°,PM=PN,MN=8cm,矩形ABCD的长和宽分别为8cm和2cm,C点和M点重合,BC和MN在一条直线上。令Rt△PMN不动,矩形ABCD沿MN所在直线向右以每秒1cm的速度移动(如图2),直到C点与N点重合为止。设移动x秒后,矩形ABCD与△PMN重叠部分的面积为y
5、如图1,Rt△PMN中,∠P=90°,PM=PN,MN=8cm,矩形ABCD的长和宽分别为8cm和2cm,C点和M点重合,BC和MN在一条直线上。令Rt△PMN不动,矩形ABCD沿MN所在直线向右以每秒1cm的速度移动(如图2),直到C点与N点重合为止。设移动x秒后,矩形ABCD与△PMN重叠部分的面积为y![]() 。求y与x之间的函数关系式。
。求y与x之间的函数关系式。
能力训练
1、如图,在平面直角坐标系内,已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.
(1) 求直线AB的解析式;
(2) 当t为何值时,△APQ与△AOB相似?
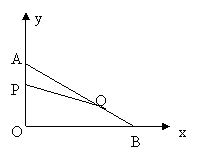 (3) 当t为何值时,△APQ的面积为
(3) 当t为何值时,△APQ的面积为![]() 个平方单位?
个平方单位?
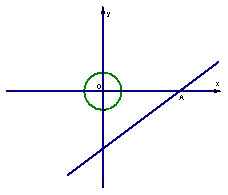
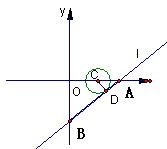
2、已知:如图所示,直线![]() 的解析式为
的解析式为![]() ,并且与
,并且与![]() 轴、
轴、![]() 轴分别相交于点A、B。
轴分别相交于点A、B。
(1) 求A、B两点的坐标。
(2) 一个圆心在坐标原点、半径为1的圆,以0.4个单位/每秒的速度向![]() 轴正方向运动,问什么时刻该圆与直线
轴正方向运动,问什么时刻该圆与直线![]() 相切;
相切;
(3) 在题(2)中,若在圆开始运动的同时,一动点P从B点出发,沿BA方向以0.5个单位/秒的速度运动,问在整个运动的过程中,点P在动圆的园面(圆上和圆的内部)上一共运动了多出时间?
3、已知二次函数的图象如图所示。
⑴ 求二次函数的解析式及抛物线顶点M的坐标;
⑵ 若点N为线段BM上的一点,过点N作![]() 轴的垂线,垂足为点Q。当点N在线段BM上运动时(点N不与点B,点M重合),设NQ的长为
轴的垂线,垂足为点Q。当点N在线段BM上运动时(点N不与点B,点M重合),设NQ的长为![]() ,四边形NQAC的面积为
,四边形NQAC的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式及自变量
之间的函数关系式及自变量![]() 的取值范围;
的取值范围;
⑶ 在对称轴右侧的抛物线上是否存在点P,使△PAC为直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由;
⑷ 将△OAC补成矩形,使上△OAC的两个顶点成为矩形一边的两个顶点,第三个顶点落在矩形这一边的对边上,试直接写出矩形的未知的顶点坐标(不需要计算过程)。

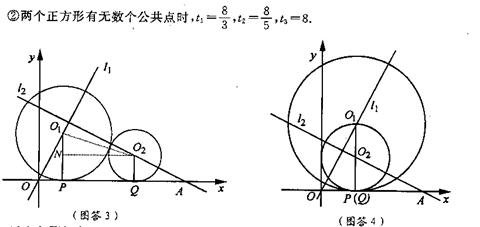
4、如图,已知直线y = 2x(即直线![]() )和直线
)和直线![]() (即直线
(即直线![]() ),
),![]() 与x轴相交于点A。点P从原点O出发,向x轴的正方向作匀速运动,速度为每秒1个单位,同时点Q从A点出发,向x轴的负方向作匀速运动,速度为每秒2个单位。设运动了t秒.
与x轴相交于点A。点P从原点O出发,向x轴的正方向作匀速运动,速度为每秒1个单位,同时点Q从A点出发,向x轴的负方向作匀速运动,速度为每秒2个单位。设运动了t秒.
(1)求这时点P、Q的坐标(用t表示).
(2)过点P、Q分别作x轴的垂线,与![]() 、
、![]() 分别相交于点O1、O2(如图16).
分别相交于点O1、O2(如图16).
①以O1为圆心、O1P为半径的圆与以O2为圆心、O2Q为半径的圆能否相切?若能,求出t值;若不能,说明理由.
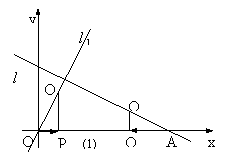 ②以O1为圆心、P为一个顶点的正方形与以O2为中心、Q为一个顶点的正方形能否有无数个公共点?若能,求出t值;若不能,说明理由。
②以O1为圆心、P为一个顶点的正方形与以O2为中心、Q为一个顶点的正方形能否有无数个公共点?若能,求出t值;若不能,说明理由。
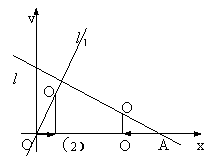
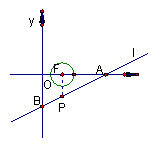
5、如图,已知直角坐标系内的梯形AOBC(O为原点),AC∥OB,OC⊥BC,AC,OB的长是关于x的方程x2-(k+2)x+5=0的两个根,且S△AOC:S△BOC=1:5。
(1)填空:0C=________,k=________;
 (2)求经过O,C,B三点的抛物线的另一个交点为D,动点P,Q分别从O,D同时出发,都以每秒1个单位的速度运动,其中点P沿OB由O→B运动,点Q沿DC由D→C运动,过点Q作QM⊥CD交BC于点M,连结PM,设动点运动时间为t秒,请你探索:当t为何值时,△PMB是直角三角形。
(2)求经过O,C,B三点的抛物线的另一个交点为D,动点P,Q分别从O,D同时出发,都以每秒1个单位的速度运动,其中点P沿OB由O→B运动,点Q沿DC由D→C运动,过点Q作QM⊥CD交BC于点M,连结PM,设动点运动时间为t秒,请你探索:当t为何值时,△PMB是直角三角形。
6.已知抛物线y=-x2-2kx+3k2(k>0)交x轴于A、B两点,交y轴于点C,以AB 为直径的⊙E交y轴于点D、F(如图),且DF=4,G 是劣弧![]() 上的动点(不与点A、D重合),直线CG交x轴于点P.
上的动点(不与点A、D重合),直线CG交x轴于点P.
(1) 求抛物线的解析式;
(2) 当直线 CG是⊙E的切线时,求tan∠PCO的值.
(3)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 当直线CG是⊙E的割线时,作GM⊥AB,垂足为H,交PF于点M,交⊙E于另一点N,设MN=t,GM=u,求u关于t的函数关系式.
当直线CG是⊙E的割线时,作GM⊥AB,垂足为H,交PF于点M,交⊙E于另一点N,设MN=t,GM=u,求u关于t的函数关系式.
 | |||
 | |||
7、如图,已知矩形ABCD的边长AB=2,BC=3,点P是AD边上的一动点(P异于A、D),Q是BC边上的任意一点. 连AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.
(1)求证:△APE∽△ADQ;
(2)设AP的长为x,试求△PEF的面积S△PEF关于x的函数关系式,并求当P在何处时,S△PEF取得最大值?最大值为多少?
 (3)当Q在何处时,△ADQ的周长最小?(须给出确定Q在何处的过程或方法,不必给出证明)
(3)当Q在何处时,△ADQ的周长最小?(须给出确定Q在何处的过程或方法,不必给出证明)
8、如图,在直角坐标系中,O是原点,A、B、C三点的坐标分别为A(18,0),B(18,6),C(8,6),四边形OABC是梯形,点P、Q同时从原点出发,分别坐匀速运动,其中点P沿OA向终点A运动,速度为每秒1个单位,点Q沿OC、CB向终点B运动,当这两点有一点到达自己的终点时,另一点也停止运动。
⑴ 求出直线OC的解析式及经过O、A、C三点的抛物线的解析式。
⑵ 试在⑴中的抛物线上找一点D,使得以O、A、D为顶点的三角形与△AOC全等,请直接写出点D的坐标。
⑶ 设从出发起,运动了t秒。如果点Q的速度为每秒2个单位,试写出点Q的坐标,并写出此时t的取值范围。
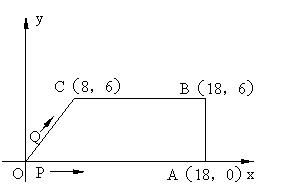 ⑷ 设从出发起,运动了t秒。当P、Q两点运动的路程之和恰好等于梯形OABC的周长的一半,这时,直线PQ能否把梯形的面积也分成相等的两部分,如有可能,请求出t的值;如不可能,请说明理由。
⑷ 设从出发起,运动了t秒。当P、Q两点运动的路程之和恰好等于梯形OABC的周长的一半,这时,直线PQ能否把梯形的面积也分成相等的两部分,如有可能,请求出t的值;如不可能,请说明理由。
答案:
练习一
1、
t=1s t= 4s
 重叠部面积为9πcm
重叠部面积为9πcm
t=7s t=16s
重叠部分面积为(9![]() +6π)cm2
+6π)cm2
2、(1)∵四边形ABCD是正方形∴∠A=∠B=90°,
 ∴AF、BP都是⊙O的切线,
∴AF、BP都是⊙O的切线,
又∵PF是⊙O的切线
∴FE=FA,PE=PB
∴四边形CDFP的周长为:
AD+DC+CB=2×3=6
(2 ) 连结OE,PF是⊙O的切线
∴OE⊥PF.在 Rt△AOF和Rt△EOF中,
∵AO=EO,OF=OF
∴Rt△AOF≌Rt△EOF ∴∠AOF=∠EOF,
同理∠BOP=∠EOP,∴∠EOF+∠EOP=![]() 180°=90°,∠FOP=90°
180°=90°,∠FOP=90°
即OF⊥OP,∴AF·BP=EF·PE=OE2=1
(3 )存在。∵∠EOF=∠AOF,∴∠EHG=∠AOE=2∠EOF,
∴当∠EFO=∠EHG=2∠EOF, 即∠EOF=30°时,Rt△EFO∽Rt△EHG
此时,∠EOF=30°, ∠BOP=∠EOP=90°-30°=60°∴BP=OB·![]() 、
、
3.

4、解(1)如图3,过点P作PM⊥BC,垂足为M,则四边形PDCM为矩形。
∴PM=DC=12 ∵QB=16-t,
∵QB=16-t,
∴S=![]() ×12×(16-t)=96-t
×12×(16-t)=96-t
(2)由图可知:CM=PD=2t,CQ=t。以B、P、Q三点为顶点的三角形是等腰三角形,可以分三种情况:
①若PQ=BQ。在Rt△PMQ中,![]() ,
,
由PQ2=BQ2 得 ![]() ,解得t=
,解得t=![]() ;
;
②若BP=BQ。在Rt△PMB中,![]() 。由BP2=BQ2 得:
。由BP2=BQ2 得:
![]() 即
即![]() 。
。
由于Δ=-704<0
∴![]() 无解,∴PB≠BQ
无解,∴PB≠BQ
③若PB=PQ。由PB2=PQ2,得![]()
整理,得![]() 。解得
。解得![]() (不合题意,舍去)
(不合题意,舍去)
综合上面的讨论可知:当t=![]() 秒时,以B、P、Q三点为顶点的三角形是等腰三角形。
秒时,以B、P、Q三点为顶点的三角形是等腰三角形。
(3)如图4,由△OAP∽△OBQ,得![]()
∵AP=2t-21,BQ=16-t,∴2(2t-21)=16-t。
 ∴t=
∴t=![]() 。
。
过点Q作QE⊥AD,垂足为E,
∵PD=2t,ED=QC=t,∴PE=t。
在RT△PEQ中,tan∠QPE=![]()
 (4)设存在时刻t,使得PQ⊥BD。如图5,
(4)设存在时刻t,使得PQ⊥BD。如图5,
过点Q作QE⊥ADS,垂足为E。
由Rt△BDC∽Rt△QPE,得
![]() ,即
,即![]() 。解得t=9
。解得t=9
所以,当t=9秒时,PQ⊥BD。
5、(1)如图1,连结OE、OF并延长分别交直线BC于N、Q。
当点P从点E运动到点F时,点K从点N运动到了点Q。
∵O、E分别为AD、AB的中点,∠A=90°,
∴∠AOE=45°。
过点O作OT⊥BC于T,则∠OTN=90°,
又∵ABCD是正方形,∴OT⊥AD,∠NOT=45°。
∴△OTN是等腰直角三角形,OT=NT=2。
同理,TQ=2。
∴NQ=4,即点K运动了4个单位长度。
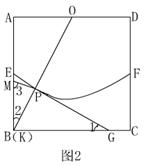 (2)①如图2,当K与B重合时,
(2)①如图2,当K与B重合时,
∵MG与![]() 所在的圆相切于点P,∴OB⊥MG,
所在的圆相切于点P,∴OB⊥MG,
∴∠2+∠3=90°。
∵∠1+∠3=90°,∴∠1=∠2。
∴Rt△BAO~Rt△GMB.
∴![]()
![]()
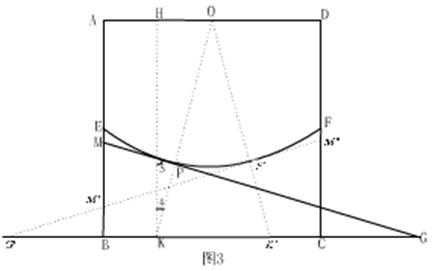
②存在BG:BM=3的情况,分析如下:
如图3,假定存在这样的点P,使得BG:BM=3
过K作KH⊥OA于H,
那么,四边形ABKH为矩形,即有KH=AB=2
∵MG与![]() 所在的圆相切于点P,∴OK⊥MG于P。
所在的圆相切于点P,∴OK⊥MG于P。
∴∠4+∠5=90°
又∵∠G+∠5=90°,∴∠4=∠G。
又∵∠OHK=∠GBM=90°,∴△OHK~△MBG。
∴![]() 。
。
∴OH= ![]() ,
,
∴存在这样的点K,使得BG:BM=3。
∴在点P运动的过程中,存在BG:BM=3的情况。
同样的,可以证明:在线段BC、CD及CB的延长线上,存在这样的点![]() 、
、![]() 、
、![]() 使得
使得![]() :
:![]() 。
。
连结![]() 交AB于点
交AB于点![]() 则
则![]() :
:![]() =
=![]() :
:![]() =3,
=3,
此时![]() =BC
=BC![]() ∴BK的值为
∴BK的值为![]()
由此可以猜想,存在BG:BM=n(n为正整数)的情况。
练习二
1、(1)在梯形ABCD中,AD∥BC、ÐB=90º过D作DE^BC于E点
∴AB∥DE
∴四边形ABED为矩形,DE=AB=12cm
在Rt△DEC中,DE=12cm,DC=13cm
∴EC=5cm
∴AD=BE=BC=EC=3cm
点P从出发到点C共需=8(秒)
点Q从出发到点C共需=8(秒)
又∵t≥0 ∴o≤t≤8
(2)当t=1.5(秒)时,AP=3,即P运动到D点
∴当1.5≤t≤8时,点P在DC边上
∴PC=16-2t,过点P作PM^BC于M
∴PM∥DE,∴=即=,∴PM=(16-2t)
又∵BQ=t,∴y=BQ·PM=t· (16-2t)=-t2+t
(3)当0≤t≤1.5时,△PQB的面积随着t的增大而增大;
当1.5<t≤4时,△PQB的面积随着t的增大而(继续)增大;
当4<t≤8时,△PQB的面积随着t的增大而减小。
2、⑴∵当Q在AB上时,显然PQ不垂直于AC。
当,由题意得:BP=x,CQ=2x,PC=4-x,
∴AB=BC=CA=4,∠C=600,
若PQ⊥AC,则有∠QPC=300,∴PC=2CQ
∴4-x=2×2x,∴x=,
∴当x=(Q在AC上)时,PQ⊥AC;
⑵当0<x<2时,P在BD上,Q在AC上,过点Q作QH⊥BC于H,
∵∠C=600,QC=2x,∴QH=QC×sin600=x
∵AB=AC,AD⊥BC,∴BD=CD=BC=2
∴DP=2-x,∴y=PD·QH=(2-x)·x=-
⑶当0<x<2时,在Rt△QHC中,QC=2x,∠C=600,
∴HC=x,∴BP=HC
∵BD=CD,∴DP=DH,
∵AD⊥BC,QH⊥BC,∴AD∥QH,
∴OP=OQ
∴S△PDO=S△DQO,
∴AD平分△PQD的面积;
⑷显然,不存在x的值,使得以PQ为直径的圆与AC相离
当x=或时,以PQ为直径的圆与AC相切。
当0≤x<或<x<或<x≤4时,以PQ为直径的圆与AC相交。
3、 (1) 当点P运动2秒时,AP=2 cm,由∠A=60°,知AE=1,PE=![]() .
.
∴ SΔAPE=![]() .
.
(2) ① 当0≤t≤6时,点P与点Q都在AB上运动,设PM与AD交于点G,QN与AD交于点F,则AQ=t,AF=![]() ,QF=
,QF=![]() ,AP=t+2,AG=1+
,AP=t+2,AG=1+![]() ,PG=
,PG=![]() .
.
∴ 此时两平行线截平行四边形ABCD的面积为S=![]() .
.
当6≤t≤8时,点P在BC上运动,点Q仍在AB上运动.
设PM与DC交于点G,QN与AD交于点F,
则AQ=t,AF=![]() ,DF=4-
,DF=4-![]() ,QF=
,QF=![]() ,BP=t-6,CP=10-t,PG=
,BP=t-6,CP=10-t,PG=![]() ,
,
而BD=![]() ,故此时两平行线截平行四边形ABCD的面积为
,故此时两平行线截平行四边形ABCD的面积为
S=![]() .
.
当8≤t≤10时,点P和点Q都在BC上运动.
设PM与DC交于点G,QN与DC交于点F,
则CQ=20-2t,QF=(20-2t)![]() ,CP=10-t,PG=
,CP=10-t,PG=![]() .
.
∴ 此时两平行线截平行四边形ABCD的面积为S=![]() .
.
故S关于t的函数关系式为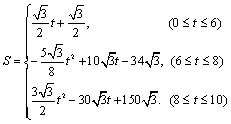
②(附加题)当0≤t≤6时,S的最大值为![]() ;
;
当6≤t≤8时,S的最大值为![]() ;
;
当8≤t≤10时,S的最大值为![]() ;
;
所以当t=8时,S有最大值为![]() .
.
4、(1)S△PCQ=![]() PC·CQ=
PC·CQ=![]() =
=![]() =2,
=2,
解得 ![]() =1,
=1,![]() =2
=2
∴当时间![]() 为1秒或2秒时,S△PCQ=2厘米2;
为1秒或2秒时,S△PCQ=2厘米2;
(2)①当0<![]() ≤2时,S=
≤2时,S=![]() =
=![]() ;
;
②当2<![]() ≤3时, S=
≤3时, S=![]() =
=![]() ;
;
③当3<![]() ≤4.5时,S=
≤4.5时,S=![]() =
=![]() ;
;
(3)有;
①在0<![]() ≤2时,当
≤2时,当![]() =
=![]() ,S有最大值,S1=
,S有最大值,S1=![]() ;
;
②在2<![]() ≤3时,当
≤3时,当![]() =3,S有最大值,S2=
=3,S有最大值,S2=![]() ;
;
③在3<![]() ≤4.5时,当
≤4.5时,当![]() =
=![]() ,S有最大值,S3=
,S有最大值,S3=![]() ;
;
 ∵S1<S2<S3 ∴
∵S1<S2<S3 ∴![]() =
=![]() 时,S有最大值,S最大值=
时,S有最大值,S最大值=![]() .
.
5、在Rt△PMN中,∵PM=PN,∠P=90°,
∴∠PMN=∠PNM=45°,
延长AD分别交PM、PN于点G、H,过点G作GF⊥MN于F,过点H作HT⊥MN于T,
∵DC=2cm,∴MF=GF=2cm,TN=HT=2cm,
∵MN=8cm,∴MT=6cm,
因此,矩形ABCD以每秒1cm的速度由开始向右移动到停止,和Rt△PMN重叠部分的形状可分为下列三种情况:
(1)当C点由M点运动到F点的过程中(![]() ,如图①所示,设CD与PM交于点E,则重叠部分图形是Rt△MCE,且MC=EC=x,
,如图①所示,设CD与PM交于点E,则重叠部分图形是Rt△MCE,且MC=EC=x,
∴![]() (
(![]() )
)
 (2)当C点由F点运动到T点的过程中 (
(2)当C点由F点运动到T点的过程中 (![]() ),如图②所示,重叠部分是直角梯形MCDG,
),如图②所示,重叠部分是直角梯形MCDG,
∵MC=x,MF=2,∴FC=DG=x-2,且DC=2,
∴![]() (
(![]() );
);
 (3)当C点由T点运动到N点的过程中(
(3)当C点由T点运动到N点的过程中(![]() ), 如图③所示,设CD与PN交于点Q,则重叠部分是五边形MCQHG,∵MC=x,∴CN=CQ=8-x,且DC=2,
), 如图③所示,设CD与PN交于点Q,则重叠部分是五边形MCQHG,∵MC=x,∴CN=CQ=8-x,且DC=2,
∴![]() (
(![]() )。
)。
能力训练
1、解:(1)设直线AB的解析式为y=kx+b
![]()
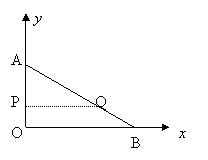 由题意,得 b=6
由题意,得 b=6
8k+b=0
解得 k=-![]() b=6
b=6
所以,直线AB的解析式为y=-![]() x+6.
x+6.
(2)由 AO=6, BO=8 得 AB=10
所以AP=t ,AQ=10-2t
1° 当∠APQ=∠AOB时,△APQ∽△AOB.
 所以
所以 ![]() =
=![]() 解得 t=
解得 t=![]() (秒)
(秒)
2° 当∠AQP=∠AOB时,△AQP∽△AOB.
所以 ![]() =
=![]() 解得 t=
解得 t=![]() (秒)
(秒)
(3)过点Q作QE垂直AO于点E.
 在Rt△AOB中,Sin∠BAO=
在Rt△AOB中,Sin∠BAO=![]() =
=![]()
在Rt△AEQ中,QE=AQ·Sin∠BAO=(10-2t)·![]() =8-
=8-![]() t
t
所以,S△APQ=![]() AP·QE=
AP·QE=![]() t·(8-
t·(8-![]() t)
t)
=-![]() +4t=
+4t=![]()
解得t=2(秒)或t=3(秒).
 2、(1)在
2、(1)在![]() 中,令x=0,得y= -3;令y=0,得x=4,
中,令x=0,得y= -3;令y=0,得x=4,
故得A、B两的坐标为A(4,0),B(0,-3)
(2)若动圆的圆心在C处时与直线![]() 相切,设切点为D,如图所示。
相切,设切点为D,如图所示。
连接CD,则CD⊥AD
由∠CAD=∠BAO,∠CDA=∠BOA=Rt∠,可知Rt△ACD∽Rt△ABO
∴![]() 即
即![]() ,则AC=
,则AC=![]()
此时OC=![]() (秒)
(秒)
根据对称性,圆C还可能在直线![]() 的右侧,与直线
的右侧,与直线![]() 相切,
相切,
此时OC=![]()
![]() (秒)答:(略)
(秒)答:(略)
(3)(3)设在t秒,动圆的圆心在F点处,动点在P处,
此时OF=0.4t,BP=0.5t,F点的坐标为(0.4t,0),连接PF,
∵![]()
又![]() ,∴
,∴![]() ,
,
∴FP∥OB,∴PF⊥OA
∴P点的横坐标为0.4t,又∵P点在直线AB上,
∴P点的纵坐标为0.3t -3,
可见:当PF=1时,P点在动圆上,当0≤PF<1时,P点在动圆内
 当P=1时,由对称性可知,有两种情况:
当P=1时,由对称性可知,有两种情况:
①当P点在x轴下方时,PF=-(0.3t
-3)=1,解之得:![]()
②当P点在x轴上方时,PF=0.3t -3=1,解之得:![]()
∴当时![]() 时,0≤PF≤1,此时点P在动圆的圆面上,所经过的时间为
时,0≤PF≤1,此时点P在动圆的圆面上,所经过的时间为![]() ,答:动点在动圆的圆面上共经过了
,答:动点在动圆的圆面上共经过了![]() 秒。
秒。
3、解:(1)设抛物线的解析式![]()
![]() ,
,
![]() 其顶点M的坐标是
其顶点M的坐标是![]() ;
;
(2)设线段BM所在的直线的解析式为![]() 点N的坐标为N
点N的坐标为N![]()
则![]()
![]() 解它们组成的方程组得
解它们组成的方程组得![]()
所以线段BM所在的直线的解析式为![]()
其中![]()
![]()
∴![]() 与
与![]() 间的函数关系为
间的函数关系为![]() ,自变量的取值围
,自变量的取值围![]()
(3)存在符合条件的点P,且坐标是![]()
![]()
![]() .
.
设点P的坐标为P![]() ,则
,则![]()
PC2=![]() 分以下几种情况讨论:
分以下几种情况讨论:
(ⅰ)若![]() 则PC2=PA2+AC2。可得
则PC2=PA2+AC2。可得![]()
![]() ,解之得
,解之得![]() (舍去)。
(舍去)。
所以点![]() 。
。
(ⅱ)若![]()
![]() 解得:
解得:![]() (舍去)。
(舍去)。
所以点![]() 。
。
(ⅲ)由图象观察得,当点P在对称轴右侧时,PA>AC,
所以边AC的对角![]() 不可能直角
不可能直角
4、

5、


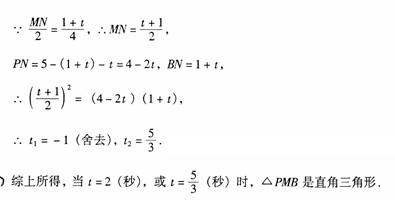
6、(1)解方程 -x2 -2kx + 3k2 = 0.
得x1=-3k,x2=k
由题意知OA = -3k = 3k,OB = k = k.
∵直径AB⊥DF. ∴OD=OF=![]() DF= 2 .
DF= 2 .
∵![]() ,
,
∴3k·k = 2×2,得k = ±![]() (负的舍去).
(负的舍去).
则所求的抛物线的解析式为![]() .
.
(2)由(1)可知AO=![]() ,AB=
,AB=![]() ,EG=
,EG=![]() ,OC=3k2 = 4.
,OC=3k2 = 4.
连结EG,
∵CG切⊙E于G,∴∠PGE=∠POC=90°,
∴Rt△PGE∽Rt△POC.∴![]() .(﹡)
.(﹡)
由切割线定理得![]() .
.
PO = PA+AO = PA +![]() .
.
代入(﹡)式整理得PA2
+ ![]() PA-6 = 0.
PA-6 = 0.
解得PA = 3-![]() (∵PA>0).
(∵PA>0).
∴tan∠PCO=![]()
∴GN∥CF,∴△PGH∽△PCO,
∴![]() .
.
同理![]() .∴
.∴![]() .
.
∵CO = 4,OF = 2,∴HM =![]() GH =
GH =![]() HN = MN,
HN = MN,
∴GM=3MN,即u =
3t(0<t≤![]() )
)
7、(1)证∠APE=∠ADQ,∠AEP=∠AQD.
(2)注意到△APE∽△ADQ与△PDE∽△ADQ,及S△PEF=![]() ,
,
得S△PEF=![]() =
=![]() . ∴当
. ∴当![]() ,
,
即P是AD的中点时,S△PEF取得最大值![]() .
.
(3)作A关于直线BC的对称点A′,连DA′交BC于Q,
则这个点Q就是使△ADQ周长最小的点,此时Q是BC的中点.
8、⑴∵O、C两点的坐标分别为O![]() ,C
,C![]()
设OC的解析式为![]() ,将两点坐标代入得:
,将两点坐标代入得:
![]() ,
,![]() ,∴
,∴![]()
∵A,O是![]() 轴上两点,故可设抛物线的解析式为
轴上两点,故可设抛物线的解析式为![]()
再将C![]() 代入得:
代入得:![]()
∴![]() ⑵D
⑵D![]()
⑶当Q在OC上运动时,可设Q![]() ,
,
依题意有:![]()
∴![]() ,∴Q
,∴Q![]() ,
,![]()
当Q在CB上时,Q点所走过的路程为![]() ,
,
∵OC=10,∴CQ=![]()
∴Q点的横坐标为![]() ,
,
∴Q![]() ,
,![]()
⑷∵梯形OABC的周长为44,当Q点OC上时,P运动的路程为![]() ,
,
则Q运动的路程为![]()
△OPQ中,OP边上的高为:![]()
梯形OABC的面积=![]() ,
,
依题意有:![]()
整理得:![]()
∵△=![]() ,∴这样的
,∴这样的![]() 不存在
不存在
当Q在BC上时,Q走过的路程为![]() ,
,
∴CQ的长为:![]()
∴梯形OCQP的面积=![]() =36≠84×
=36≠84×![]()
∴这样的![]() 值不存在
值不存在
综上所述,不存在这样的![]() 值,使得P,Q两点同时平分梯形的周长和面积
值,使得P,Q两点同时平分梯形的周长和面积