中考数学升学模拟考试

中考数学升学模拟考试（二）

数　学　试　卷

第Ⅰ卷（机读卷　共32分）

考 生 须 知

1． 第Ⅰ卷为选择题，只有一道大题，共2页。答题前要认真审题，看清题目要求，按要求认真作答。 2． 第Ⅰ卷各题均须按规定要求在“机读答题卡”上作答，题号要对应，填涂要规范。 3.  考试结束后，考生应将试卷和“机读答题卡”一并交监考老师收回。

一、选择题（共8个小题，每小题4分，共32分）

　　　下列各题均有四个选项,其中只有一个是符合题意的,用铅笔把”机读答题卡”上对应题目答案的相应字母处涂黑.

1. 下列各组数中，互为相反数的是

　A.　-2与　 　B. 与2　　 C. -2与　 　D. -2与

2．下列各式计算正确的是

　　A．  B．  C． 　D．　  　　　　　　　　　　　　　　　　　　　 

3. 在ΔABC中，∠A和∠B都是锐角，且，，则ΔABC三个角的大小关系是

　 A. ∠C>∠A>∠B　　　　　　　　　　　　B.  ∠C>∠B>∠A

C. ∠A>∠B>∠C　　　　　　　　　　　　D.  ∠B>∠C>∠A　

4. 某鞋店试销一种新款运动鞋,试销期间销售情况如下表:

型 号	22	22.5	23	23.5	24	24.5	25
数量(双)	3	5	10	15	8	3	2

　对于这个鞋店的经理来说最关心的是哪种型号的鞋畅销,则下列统计量对鞋店经理来说最有意义的是

A. 平均数B. 众数  C. 中位数　　　　　 D. 标准差

　　　　　　　　　　　　　　　　　　

5．已知矩形的面积为10，则它的长与宽之间的关系用图象大致可表示为

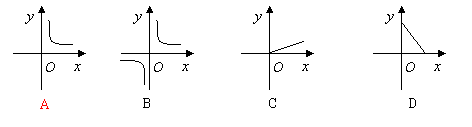6．若“！”是一种数学运算符号，并且1！= 1，2！= 2×1= 2，3！= 3×2×1= 6，

4！= 4×3×2×1= 24…………，则 的值为

　　 A 　　　　　　Ｂ　　　　　Ｃ 9900　　　　　Ｄ2！

7．在拼图游戏中，从图1的四张纸片中，任取两张纸片，能拼成“小房子”（如图2）的概率等于（　　）

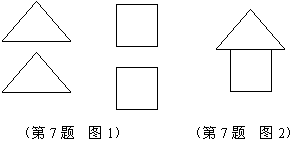Ａ．　　　　　　　 Ｂ．　　　　　　　　 Ｃ．　　　　　　　　 Ｄ．

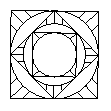
8．夏都广场地面喷泉的喷头用铸铁防护罩保护，防护罩的图案如下图所示，外圈是正方形。正方形的对角线长为2，在正方形内作一个内切圆；在第一个内切圆内又作一个内接正方形，在正方形内再作第二个内切圆；然后又在第二个内切圆中作内接正方形，在正方形内再作第三个内切圆，　依此作到第个内切圆，它的半径是（　　）

 A 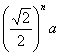 　　　B 　　　C　　　　 Ｄ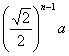

第Ⅱ卷（非机读卷　共88分）

考生须知	1．　 考生认真填写密封线内的区县名、学校名、姓名、报名号、准考证号。 2．　 第Ⅱ卷包括五道大题，共7页。答题前要认真审题，看清题目要求，按 要求认真作答。 3．　 答题时字迹要工整，画图要清晰，卷面要整洁。 4．　 除画图可以用铅笔外，答题必须用黑色或蓝色钢笔、圆珠笔。

题号	二	三	四	五	总分
得分
阅卷人
复查人

二、填空题（共4个小题，每小题4分，共16分）

9．分解因式：=　　　　　　　　　  .　

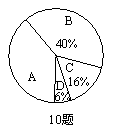
10．某校九年级（1）班有50名同学，综合素质评价

“运动与健康”方面的等级统计如图所示，则该班

“运动与健康”评价等级为的人数是　　　　　　．

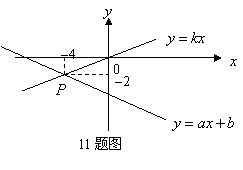11．如图，已知函数和的图象交于点，则根据图象可得，关于的二元一次方程组的解是 　　 ．

12．从边长为的大正方形纸板中挖去一个边长为　的小 正方形后，将其裁成四个相同的等腰梯形（如图甲），然后拼成一个平行四边形（如图乙）．那么通过计算阴影部分的面积可以验证公式______________．

三、(共6个小题, 每小题5分,共30分)

  13. 计算：

14. 先化简，再求值：，其中 =．

15．已知方程的解是，求关于的方程的解．

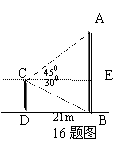
16．在旧城改造中，要拆除一烟囱AB，在地面上事先画定以B为圆心，半径与AB等长的圆形危险区。现在从离B点21米远的建筑物CD顶端C点测得A点的仰角为45⁰，B点的俯角是30⁰；问离B点35米远的国家级保护文物是否在危险区内？　　　　  

17．某服装厂准备加工300套演出服．在加工60套后，采用了新技术，使每天的加工量是原来的2倍，结果共用9天完成任务．求该厂原来每天加工多少套演出服．

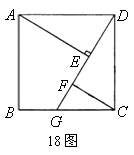
18．如图，四边形是正方形，是上任意一点（点与不重合），于，交于．

（1）在图中找出一对全等三角形，并加以证明；

（2）求证：．

四、（共4个小题，每小题5分,共20分）

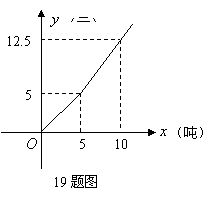
19．为了鼓励市民节约用水，自来水公司特制定了新的用水收费标准，每月用水量（吨）与应付水费（元）的函数关系如图．

（1）求出当月用水量不超过5吨时，与之间的函数关系式；

（2）某居民某月用水量为8吨，求应付的水费是多少元？

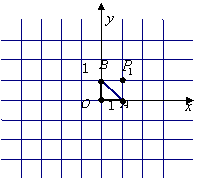
20．如果将点P绕定点M旋转180°后与点Q重合，那么称点P与点Q关于点M对称，定点M叫做对称中心．此时，点M是线段PQ的中点．如图，在直角坐标系中，△ABO的顶点A、B、O的坐标分别为（1，0）、（0，1）、（0，0）．点列P₁，P₂，P₃，…中的相邻两点都关于△ABO的一个顶点对称：点P₁与点P₂关于点A对称，点P₂与点P₃关于点B对称，点P₃与点P₄关于点O对称，点P₄与点P₅关于点A对称，点P₅与点P₆关于点B对称，点P₆与点P₇关于点O对称，…，

对称中心分别是A，B，O，A，B，O，…，且这些对称中心依次循环．已知点P₁的坐标是（1，1），试写出点P₂、P₇、P₁₀₀的坐标．

21．在今年“五一”长假期间，某学校团委会要求学生参加一项社会调查活动．八年级学生小青想了解她所居住的小区500户居民的家庭收入情况，从中随机调查了40户居民家庭的收入情况（收入取整数，单位：元）并绘制了如下的频数分布表和频数分布直方图．

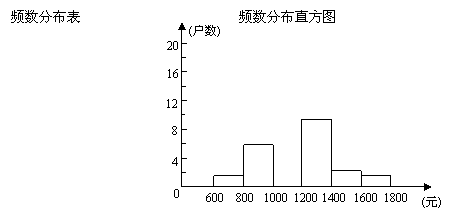分组	频数	频率
	2	0.050
	6	0.150
	18	0.450
	9	0.225
	2	0.050
合计	40	1.000

根据以上提供的信息，解答下列问题：

（1）　　  补全频数分布表：

（2）　　  补全频数分布直方图；

（3）　　  请你估计该居民小区家庭收入较低（不足1000元）的户数大约有多少户？

22．

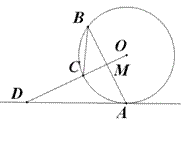
已知：如图，点A、B、C为⊙O上的点，点D在OC的延长线上，∠CBA=∠CDA=30°.

(1) 求证：AD是⊙O的切线；

(2) 若OD⊥AB于M，BC=5，求DC的长.

五 （共3个小题，共22分）

23． （本题满分7分）

如图（），两个不全等的等腰直角三角形和叠放在一起，并且有公共的直角顶点．

（1）将图（）中的绕点顺时针旋转角，在图（）中作出旋转后的（保留作图痕迹，不写作法，不证明）．

（2）在图（）中，你发现线段，的数量关系是　　　　　　　　　　　　　　　　，直线，相交成　　　　 　　　　　　　　　 度角．

（3）将图（）中的绕点顺时针旋转一个锐角，得到图（），这时（2）中的两个结论是否成立？作出判断并说明理由．若绕点继续旋转更大的角时，结论仍然成立吗？作出判断，不必说明理由．

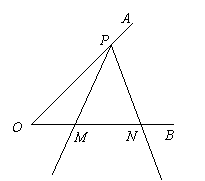
24．（本题7分）

如图，已知为的边上的一点，以为顶点的的两边分别交射线于两点，且（为锐角）．当以点为旋转中心，边与重合的位置开始，按逆时针方向旋转（保持不变）时，两点在射线上同时以不同的速度向右平行移动．设，（），的面积为．若．

（1）当旋转（即）时，求点移动的距离；

（2）求证：；

（3）求出与之间的关系式；

（4）试写出随变化的函数关系式，并确定的取值范围．

25.（本题8分）

如图，抛物线 与轴交于A、B两点，与轴交于点C，且 OA = 2， OC = 3.

⑴ 求抛物线的解析式；

⑵ 作 Rt△OBC 的高OD，延长OD与抛物线在第一象限内交于点E，求点 E 的坐标；

⑶ 在  轴上方的抛物线上，是否存在一点 P ，使得四边形OBEP是平行四边形？若存在，求出点P的坐标；若不存在，请说明理由；

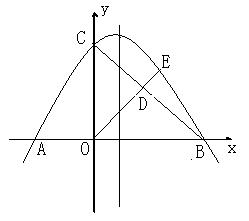⑷ 在抛物线的对称轴上，是否存在一点Q，使得 △BEQ的周长最小？若存在，求出点Q的坐标；若不存在，请说明理由