《四边形》基础测试
（一）选择题（每小题3分，共30分）
1．内角和与外角和相等的多边形是……………………………………………………（ ）
（A）三角形 （B）四边形 （C）五边形 （D）六边形【答案】B．
2．顺次连结等腰梯形各边中点所得的四边形一定是…………………………………（ ）
（A）菱形 （B）矩形
（C）梯形 （D）两条对角线相等的四边形【答案】A．
3．观察下列四个平面图形，其中中心对称图形有…………………………………（ ）
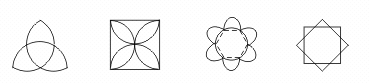
（A）2个 （B）1个 （C）4个 （D）3个
【提示】第一个图形不是中心对称图形．【答案】D．
4．已知下列四个命题：（1）对角线互相垂直平分的四边形是正方形；
（2）对角线垂直相等的四边形是菱形；（3）对角线相等且互相平分的四边形是矩形；
（4）四边都相等的四边形是正方形．其中真命题的个数是………………（ ）
（A）1 （B）2 （C）3 （D）0【提示】（3）正确．【答案】A．
5．菱形的一条对角线与它的边相等，则它的锐角等于………………………………（ ）
（A）30° （B）45° （C）60° （D）75°【答案】C．
6．下列命题中的真命题是………………………………………………………………（ ）
（A）一组对边平行，另一组对边相等的四边形是平行四边形
（B）有一组对边和一组对角分别相等的四边形是平行四边形
（C）两组对角分别相等的四边形是平行四边形
（D）两条对角线互相垂直且相等的四边形是正方形【答案】C．
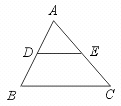
7．如图，DE是△ABC的中位线，若AD＝4，AE＝5，BC＝12，则△ADE的周长
是………………………………………………（ ）
（A）7.5 （B）30 （C）15 （D）24
【答案】C．
8．矩形的边长为10 cm和15 cm，其中一内角平分线分长边为两部分，这两部分的长
为………………………………………………………………………………………（ ）
（A）6 cm和9 cm （B）5 cm和10 cm
（C）4 cm和11 cm （D）7 cm和8 cm
【提示】长边被分成的两部分之中，有一部分与矩形短边相等．【答案】B．
9．如图，在等腰梯形ABCD中，AD∥BC，AC、BD相交于点O，则图中全等三角形
共有……………………………………………………………………………………（ ）
（A）1对 （B）3对 （C）2对 （D）4对
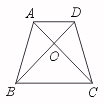
【提示】以AB和CD为对应边的两个三角形．【答案】B．
10．菱形周长为20 cm，它的一条对角线长6 cm，则菱形的面积为…………………（ ）
（A）6 （B）12 （C）18 （D）24
【提示】若菱形两对角线为a和b，则S菱形＝
．【答案】D．
（二）填空题（每小题3分，共24分）
11．如图，在□ABCD中，则对角线AC、BD相交于O，图中全等的三角形共有____对．
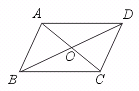
【提示】考察以AB、CD为对应边的三角形，有3对全等三角形；抹去AB、CD两边，又有1对全等三角形．【答案】4．
12．如果一个多边形的每个内角都等于108°，那么这个多边形是_____边形．
【提示】360°÷每个外角的度数．【答案】5．
13．梯形的上底边长为5，下底边长为9，中位线把梯形分成上、下两部分，则这两部分的
面积的比为_______．【提示】先算出中位线的长，然后用梯形面积公式计算．【答案】
．
14．如图，等腰梯形ABCD中，AD∥BC，∠B＝45°，AE⊥BC于点E，AE＝AD＝2 cm，
则这个梯形的中位线长为_____cm．
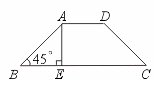
【提示】BC＝6 cm．【答案】4．
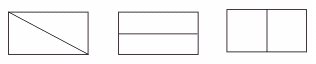
15．请画出把下列矩形的面积二等分的直线，并填空（一个矩形只画一条直线，不写画
法）．在一个矩形中，把此矩形面积二等分的直线最多有_____条，这些直线都必须经过此矩形的_____点．
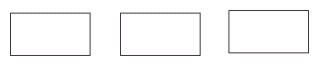
【答案】无数；对称中心（或两条对角线的交点）．
16．如图，在梯形ABCD中，AD∥BC，中位线EF分别与BD、AC交于点G、H．若
AD＝6，BC＝10，则GH的长是______．
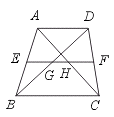
【答案】2．
17．如图，矩形ABCD中，O是两对角线的交点AE⊥BD，垂足为E．若OD＝2 OE，
AE＝
，则DE的长为______．
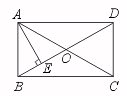
【提示】OA＝OD＝2 OE，用勾股定理求出OE和OA的长．
【答案】3．
18．如图，在□ABCD中，AE⊥BC于E，AF⊥CD于F，若AE＝4，AF＝6，□ABCD
的周长为40，则S□ABCD为______．
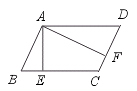
【提示】在□ABCD中，AE·BC＝AF·CD＝S□ABCD，BC＋CD＝20，求BC或CD．
【答案】48．
（三）证明题（每小题5分，共20分）
19．已知：如图，在梯形ABCD中，AD∥BC，AB＝DC，P是AD中点．
求证：BP＝PC．
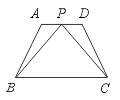
【提示】证明△ABP≌△DCP．
【答案】在梯形ABCD中，AD∥BC，
∵ AB＝DC，
∴ ∠A＝∠D．
∵ P是AD中点，
∴ AP＝DP．
在△ABP和△DCP中，
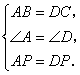
∴ △ABP≌△DCP．
∴ PB＝PC．
20．已知：如图，AD∥BC，ED∥BF，且AF＝CE．求证：四边形ABCD是平行四边
形．
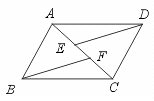
【提示】证明△ADE≌△CBF，得到AD＝BC即可．
【答案】在△ADE和△CBF中，
∵ AD∥BC，
∴ ∠DAE＝∠BCF．
∵ ED∥BF，
∴ ∠DEF＝∠BFE．
∴ ∠DEA＝∠BFC．
∵ AF＝CE，
∴ AE＝CF．
∴ △ADE≌△CBF．
∴ AD＝BC．
又 AD∥BC，
∴ 四边形ABCD是平行四边形．
21．已知：如图，矩形ABCD中，E、F是AB上的两点，且AF＝BE．
求证：∠ADE＝∠BCF．
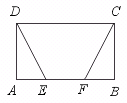
【提示】证明Rt△ADE≌Rt△BCF．
【答案】在矩形ABCD中，
∠A＝∠B＝90°，AD＝BC．
又 AF＝BE，
∴ AF－EF＝BE－EF，
即 AE＝BF．
∴ Rt△ADE≌Rt△BCF．
∴ ∠ADE＝∠BCF．
22．证明等腰梯形判定定理：在同一底上的两个角相等的梯形是等腰梯形．（要求：画出
图形，写出已知、求证、证明．）
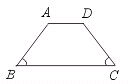
【提示】作辅助线，构造等腰三角形．
【答案】已知：在梯形ABCD中，AD∥BC，∠B＝∠C（图（1））．求证：AB＝DC．
【证法一】如图（1），过点D作DE∥AB，交BC于E．
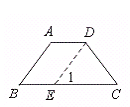
图（1）
∴ ∠B＝∠1．又 ∠B＝∠C，∴ ∠C＝1．
∴ DE＝DC．又 AB∥DE，AD∥BE，
∴ 四边形ABED为平行四边形，∴ AB＝DE．
∴ AB＝DC．
【证法二】如图（2），分别延长BA、CD，交于点E．
图（2）
∵ ∠B＝∠C，∴ BE＝CE．
∵ AD∥BC，∴ ∠B＝∠1，∠C＝∠2．
∴ ∠1＝∠2．∴ AE＝DE．
∴ BE－AE＝CE－DE，即AB＝DC．
（四）计算题（每小题6分，共12分）
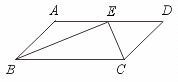
23．已知：如图，在□ABCD中，BE、CE分别平分∠ABC、∠BCD，E在AD上，
BE＝12 cm，CE＝5 cm．求□ABCD的周长和面积．
【提示】证明BE⊥EC和E为AD中点．
【答案】在□ABCD中，
∵ AB∥CD，
∴ ∠ABC＋∠BCD＝180°．
∵ ∠ABE＝∠EBC，∠BCE＝∠ECD，
∴ ∠EBC＋∠BCE＝
（∠ABC＋∠BCD）＝90°．
∴ ∠BEC＝90°．
∴ BC2＝BE2＋CE2＝122＋52＝132．
∴ BC＝13．
∵ AD∥BC，
∴ ∠AEB＝∠EBC．
∴ ∠AEB＝∠ABE．
∴ AB＝AE．
同理 CD＝ED．
∵ AB＝CD，
∴ AB＝AE＝CD＝ED＝BC＝6.5．
∴ □ABCD的周长＝2（AB＋BC）＝2（6．5＋13）＝39．
S□ABCD＝2 S△BCE＝2·BE·EC
＝12×5＝60．
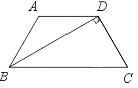
24．如图，在梯形ABCD中，AD∥BC，AB＝DC，BD⊥DC于D，且∠C＝60°，若
AD＝5 cm，求梯形的腰长．
【提示】求出∠CBD，∠ABD和∠ADC的度数，证明AB＝AD，或者过D点作DE⊥BC于E，CE为下底与上底的差的一半，又是CD的一半，CD又是BC的一半．从中找出CD与AD的关系．
【解法一】∵ BD⊥CD，∠C＝60°，
∴ ∠CBD＝30°．
在等腰梯形ABCD中，∠ABC＝∠C＝60°，
∴ ∠ABD＝∠CBD＝30°．
∵ AD∥BC，
∴ ∠ADB＝∠CBD．
∴ ∠ABD＝∠ADB．
∴ AB＝AD＝5（cm）．
【解法二】过D点作DE⊥BC，垂足为E点．
∵ 在Rt△CDE中，∠CDE＝30°，
∴ CE＝CD．
又 CE＝（BC－AD），
∴ CD＝BC－AD．
即 BC＝CD＋AD．
又 在Rt△BCD中，∠CBD＝30°，
∴ CD＝BC．
∴ CD＝2 CD－AD．
即 CD＝AD＝5（cm）．
（五）解答题（每小题7分，共14分）
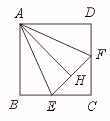
25．如图，在正方形ABCD中，点E、F分别在BC、CD上移动，但A到EF的距离
AH始终保持与AB长相等，问在E、F移动过程中：
（1）∠EAF的大小是否有变化？请说明理由．
（2）△ECF的周长是否有变化？请说明理由．
【提示】证明△EAH≌△EAB，△FAH≌△FAD．
【答案】（1）∠EAF始终等于45°．证明如下：
在△EAH和△EAB中，
∵ AH⊥EF，∴ ∠AHE＝90°＝∠B．
又 AH＝AB，AE＝AE，∴ Rt△EAH≌Rt△EAB．
∴ ∠EAH＝∠EAB．
同理 ∠HAF＝∠DAF．∴ ∠EAF＝∠EAH＋∠FAH
＝∠EAB＋∠FAD＝∠BAD＝45°．
因此，当EF在移动过程中，∠EAF始终为45°角．
（2）△ECF的周长不变．证明如下：
∵ △EAH≌△EAB，
∴ EH＝EB．
同理 FH＝FD．
∴ △ECF周长＝EC＋CF＋EH＋HF
＝EC＋CF＋BE＋DF
＝BC＋CD＝定长．
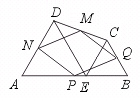
26．已知：如图，在四边形ABCD中，E为AB上一点，△ADE和△BCE都是等边三
角形，AB、BC、CD、DA的中点分别为P、Q、M、N，试判断四边形PQMN为怎样的四边形，并证明你的结论．
【提示】连结AC和CD，首先利用中位线定理和平行四边形判定定理，证明四边形PQMN为平行四边形，然后证明△AEC≌△DEB，得到AC＝BD，再证明□PQMN为菱形．
【答案】四边形PQMN为菱形．证明如下：
如图，连结AC、BD．
∵ PQ为△ABC的中位线，
∴ PQ
AC．
同理 MNAC．
∴ MNPQ，
∴ 四边形PQMN为平行四边形．
在△AEC和△DEB中，
AE＝DE，EC＝EB，∠AED＝60°＝∠CEB，
即 ∠AEC＝∠DEB．
∴ △AEC≌△DEB．
∴ AC＝BD．
∴ PQ＝AC＝BD＝PN．
∴ □PQMN为菱形．