中考数学模拟试题40
班级：_________ 姓名：_________ 得分：_________
一、填空题(每小题3分，共24分)
1．计算：-
＝______．
2．若a＜0，化简
＝______．
3．若一个三角形的三边长均满足方程x2-6x＋8＝0，则这个三角形的周长为______．
4．方程组
(x＜y)的解是______．
5．若2x2-5x＋
-5＝0，则2x2-5x-1的值为______．
6．把抛物线y＝-x2＋2的图象向下平移1个单位，再以x轴为对称轴作图象的对称图形，则所得的图象的函数解析式是______．
7．已知0°＜a ＜45°，且sin2a ＝
，
则a ＝______．
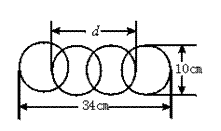
8．如图,奥迪车商标的长为34 cm，宽为10 cm，
则d的值为______．
二、选择题(每小题3分，共18分)
9．下列图形中，是中心对称图形的有( )
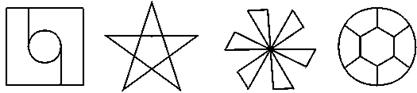
A．1个 B．2个 C．3个 D．4个
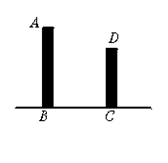10．如图，两建筑物的水平距离为a米，从A点测得D点的俯角为a ，测得C点的俯角为b ，则较低建筑物CD的高为( )
A．acotb 米 B．a(tanb -tana )米
C．a米 D．acota 米
11．一元二次方程ax2＋bx＋c＝0中，a＞0，b＜0，c＜0，则这个方程根的情况是( )
A．有两个正根 B．有两个负根
C．有一正根一负根且正根绝对值大 D．有一正根一负根且负根绝对值大
12．若一抛物线y＝ax2与四条直线x＝1、x＝2、y＝1、y＝2围成的正方形有公共点，则a的取值范围是( )
A．
≤a≤1 B．
≤a≤2 C．
≤a≤1 D．≤a≤2
13．某城市按以下规定收取每月煤气费：用煤气如果不超过10立方米，按每立方米0.80元收费；如果超过10立方米，超过部分按每立方米1.20元收费，已知某用户4月份的煤气平均每立方米0.88元，那么4月份该用户应交煤气费( )
A．9元 B．10元 C．11元 D．12.5元
14．在圆中，一条弧的长为l，半径为R，那么这条弧所对的圆心角为( )
A．
度 B．
度 C．
度 D．
度
三、解答题(15～19每小题8分，共40分)
15．如图，D是△ABC的边AC上一点，CD＝2AD，AE⊥BC交BC于点E．若BD＝8，sin∠CBD＝
，求AE的长．
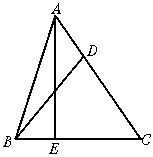
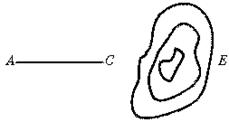
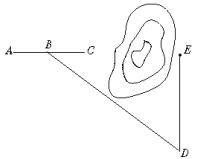
16．如图，沿AC方向开山修渠，为了加快施工进度，要在高山的另一边同时施工，请你设计一种方案，确定开挖点E的位置，使A、C、E三点在一条直线上．
17．学生甲每小时走3公里，出发1.5小时后，同学乙以每小时4.5公里的速度追甲，设乙行走的时间为t小时．
(1)写出甲、乙两同学每人所走的路程s与时间t的关系式；
(2)在同一坐标系中作出它们的图象；
(3)求出两条直线的交点坐标，并写出它的实际意义．
18．某广告公司欲招聘广告策划人员一名，对甲、乙、丙三名候选人进行了三项素质测试．他们的各项测试成绩如下表所示：
| 测试项目 | 测试成绩 | ||
| 甲 | 乙 | 丙 | |
| 创新能力 | 72 | 85 | 67 |
| 综合知识 | 50 | 74 | 70 |
| 计算机操作 | 88 | 45 | 67 |
作出判断，并说明理由
(1)如果根据三项测试的平均成绩确定录用人选，那么谁将被录用？
(2)根据实际需要，公司将创新能力、综合知识、计算机操作三项测试的得分按4∶3∶1的比例确定各人的测试成绩，此时谁将被录用？
19．已知：如图，抛物线y＝ax2＋bx＋c(a≠0)经过x轴上的两点A(x1，0)、B(x2，0)和y轴上的点C(0，-
)，⊙P的圆心P在y轴上，且经过B、C两点；若b＝
a，AB＝2，
(1)求抛物线的解析式；
(2)D在抛物线上，且C、D两点关于抛物线的对称轴对称，问直线BD是否经过圆心P？并说明理由．
(3)设直线BD交⊙P于另一点，求经过点E的⊙P的切线的解析式．
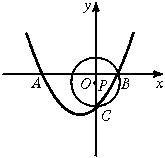
四、解答题(每题9分，共18分)
20．不过圆心的直线l交⊙O于C、D两点，AB是⊙O的直径，AE⊥l，垂足为E，BF⊥l，垂足为F．
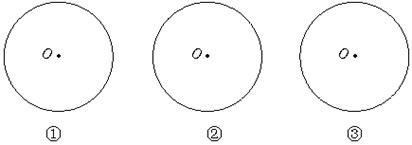
(1)在图中三个圆中分别补画出满足上述条件的具有不同位置关系的图形；
(2)请你观察(1)中所画图形，写出一个各图都具有的两条线段相等的结论(不再标注其他字母，找结论的过程中所连辅助线不能出现在结论中，不写推理过程)；
(3)请你选择(1)中的图形，证明(2)所得出的结论．
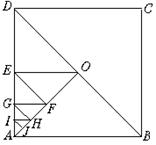
21．如图，容易知道，正方形ABCD中，当第1次作AO⊥BD时，S△AOD＝S正方形，当第2次作EO⊥AD时，S△AOE＝
S正方形；当第3次作EF⊥AO时，S△EFO＝
S正方形，……依此方法继续作垂直线段，当作到第n次时，所得的最小的三角形的面积与正方形面积之间有什么数量关系，用含n的代数式表示，并简明写出你的探求过程．
参考答案
一、1．-2 2．-a
3．6，10，12 4．
5．0或2 6．y＝x2-1 7．30° 8．18cm
二、9．C 10．B 11．C 12．D 13．C 14．B
三、15．过点D作DH⊥BC，垂足为H，在Rt△BDH中，DH＝BD·sinCBD＝8×＝6．
∵ DH⊥BC，AE⊥BC，
∴ DH∥AE，△CDH∽△CAE，
∴ 
∴ AE＝DH＝×6＝9．
16．(1)如图，在AC上取一点B，在山的另一侧取一点D，使在D点能见B点，且使∠ABD为钝角；
(2)量得BD＝m米；
(3)测得∠CBD＝a ，点E在使∠BDE＝90°-a 的方向上；
(4)点E距离点D为 msina 米．
17．(1)S甲＝3t＋4.5，S乙＝4.5t (2)略
(3)(3，13.5)．实际意义为乙追上甲所用时间为3小时，甲乙两人距出发点距离为13.5公里处相遇．
18．解：(1)甲的平均成绩为
(72＋50＋88)＝70(分)．
乙的平均成绩为(85＋74＋45)＝68(分)，
丙的平均成绩为(67＋70＋67)＝68(分)
∴ 候选人甲将被录用．
(2)甲的测试成绩为
＝67.75(分)
乙的测试成绩为
＝75.875(分)
丙的测试成绩为
＝68.125(分)
∴ 候选人乙将被录用．
19．(1)抛物线的解析式是y＝
x2＋
x-．
(2)直线BD经过圆心P．
(3)经过E点的⊙P的切线的解析式是y＝-x-2．
20．(1)
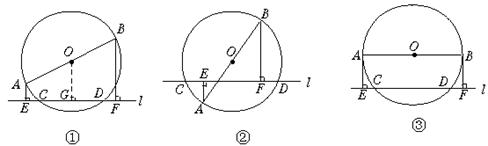
(2)EC＝FD，或ED＝FC．
(3)略
21．设第一次作AO⊥BD为n＝1．
当n＝1时，S△＝S正方形＝
S正方形＝
S正方形
当n＝2时，S△＝S正方形＝
S正方形＝
S正方形
当n＝3时，S△＝S正方形＝
S正方形＝
S正方形
……
∴ 当作到n次时，S△＝
S正方形
检验：当n＝5时，即图中GH⊥AO时，S△AHG＝
S正方形＝
S正方形．