中考数学函数及图象复习测试
学校: 姓名:
一、学习的目标:掌握正、反比例、一次函数、二次函数的图象及性质
二 、知识点归纳:
1、平面直角坐标系:平面内两条有公共原点且互相垂直的数轴构成了平面直角坐标系,坐标平面内一点对应的有序实数对叫做这点的坐标。在平面内建立了直角坐标系,就可以把“形”(平面内的点)和“数”(有序实数对)紧密结合起来。
2、函数的概念:设在某个变化过程中有两个变量x、y,如果对于x在某一范围内的每一个确定的值,y都有唯一确定的值与它相对应,那么就说y是x的函数,x叫做自变量。
3、自变量的取值范围:对于实际问题,自变量取值必须使实际问题有意义。对于纯数学问题,自变量取值应保证数学式子有意义。
4、正比例函数: 如果y=kx(k是常数,k≠0),那么,y叫做x的正比例函数.
5、、正比例函数y=kx的图象:
过(0,0),(1,K)两点的一条直线.
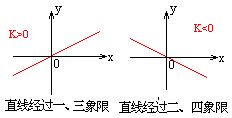
6、正比例函数y=kx的性质
(1)当k>0时,y随x的增大而增大
(2)当k<0时,y随x的增大而减小
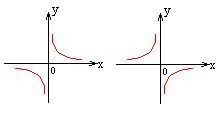
7、反比例函数及性质
![]()
(1)当k>0时,在每个象限内分别是y随x的增大而减小;
(2)当k<0时,在每个象限内分别是y随x的增大而增大.
8、一次函数 如果y=kx+b(k,b是+常数,k≠0),那么y叫做x的一次函数.
9、一次函数y=kx+b的图象
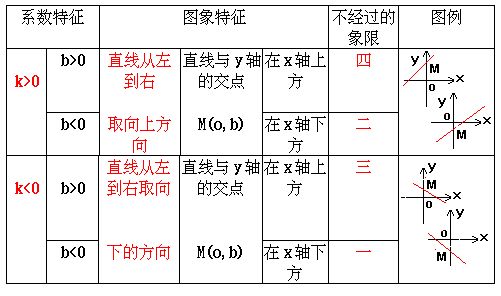
10、一次函数y=kx+b的性质
![]()
(1)当k>0时,y随x的增大而增大;
(2)当k<0时,y随x的增大而减小.
9、二次函数的性质
(1)函数y=ax![]() +bx+c(其中a、b、c是常数,且a
+bx+c(其中a、b、c是常数,且a![]() 0)叫做的二次函数。
0)叫做的二次函数。
(2)利用配方,可以把二次函数表示成y=a(x+![]() )
)![]() +
+![]() 或y=a(x-h)
或y=a(x-h)![]() +k的形式
+k的形式
(3)二次函数的图象是抛物线,当a>0时抛物线的开口向上,当a<0时抛物线开口向下。
抛物线的对称轴是直线x=-![]() 或x=h
或x=h
抛物线的顶点是(-![]() ,
,![]()
![]() )或(h,k)
)或(h,k)
三、学习的过程:
分层练习(A组)
一、选择题:
1.函数![]() 中,自变量x的取值范围是( )
中,自变量x的取值范围是( )
A.x<1 B.x>1 C.x≥1 D.x≠1
![]()
2.在函数 中,自变量的取值范围是( )
A. ![]() B.
B.
![]() C.
C. ![]() D.
D. ![]()
3.在函数![]() 中,自变量x的取值范围是
中,自变量x的取值范围是
(A)x≥3 (B)x≠3 (C)x>3 (D)x<3
4. 点P(-1,2)关于y轴对称的点的坐标是( ).
A.(1,2) B.(-1,2) C.(1,-2) D.(-1,-2)
5. 点M(1,2)关于x轴对称点的坐标为( )
A、(-1,2) B、(-1,-2) C、(1,-2) D、(2,-1)
6.在直角坐标系中,点 ![]() 一定在( )
一定在( )
A. 抛物线 ![]() 上
B. 双曲线
上
B. 双曲线 ![]() 上
上
C. 直线 ![]() 上
D. 直线
上
D. 直线 ![]() 上
上
7. 若反比例函数![]() 的图象经过点(-1,2),则k的值为
的图象经过点(-1,2),则k的值为
A.-2
B.![]() C.2
D.
C.2
D.![]()
8. 函数y=-x+3的图象经过( )
(A)第一、二、三象限 (B)第一、三、四象限
(C)第二、三、四象限 (D)第一、二、四象限
9.函数y=2x-1的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10、如图所示,函数![]() 的图象最可能是( )
的图象最可能是( )
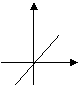 | |||||||
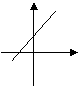 | 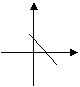 | 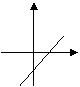 | |||||
(A) (B) (C) (D)
11.为解决药价虚高给老百姓带来的求医难的问题,国家决定对某药品分两次降价。若设平均每次降价的百分率为x,该药品的原价是m元,降价后的价格是y元,则y与x的函数关系式是( )
(A)y=2m(1-x) (B)y=2m(1+x) (C)y=m(1-x)2 (D)y=m(1+x)2
13.一辆汽车由淮安匀速驶往南京,下列图象中,能大致反映汽车距南京的路程s(千米)和行驶时间t(小时)的关系的是( )
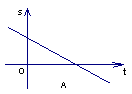
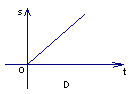
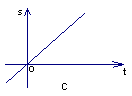
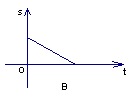
14. 8、某小工厂现在年产值150万元,计划今后每年增加20万元,年产值![]() (万元)与年数
(万元)与年数![]() 的函数关系式是( )
的函数关系式是( )
A.![]() B.
B. ![]()
C.![]() D.
D.![]()
15.关于函数![]() ,下列结论正确的是( )
,下列结论正确的是( )
(A)图象必经过点(﹣2,1) (B)图象经过第一、二、三象限
 (C)当
(C)当![]() 时,
时,![]() (D)
(D)![]() 随
随![]() 的增大而增大
的增大而增大
16.一次函数y=ax+b的图像如图所示,
则下面结论中正确的是( )
A.a<0,b<0 B.a<0,b>0
C.a>0,b>0 D.a>0,b<0
17.若反比例函数 ![]() 的图象在每一象限内,y随x的增大而增大,则有( )
的图象在每一象限内,y随x的增大而增大,则有( )
A.k≠0 B.k≠3 C.k<3 D.k>3
18. 函数![]() 的图象与坐标轴围成的三角形的面积是( )
的图象与坐标轴围成的三角形的面积是( )
A.2 B.1 C.4 D.3
19.抛物线![]() 的对称轴是( )
的对称轴是( )
A、x=-2 B、x=2 C、x=-4 D、x=4
20.抛物线y=2(x-3)2的顶点在( )
A. 第一象限 B. 第二象限 C. x轴上 D. y轴上
二、填空题:
1.抛物线![]() 与x轴分别交A、B两点,则AB的长为________.
与x轴分别交A、B两点,则AB的长为________.
2.直线![]() 不经过第_______象限.
不经过第_______象限.
3.若反比例函数![]() 图象经过点A(2,-1),则k=_______.
图象经过点A(2,-1),则k=_______.
4.若将二次函数y=x2-2x+3配方为y=(x-h)2+k的形式,则y= .
5.若反比例函数![]() 的图象过点(3,-4),则此函数的解析式为
.
的图象过点(3,-4),则此函数的解析式为
.
6.函数![]() 的自变量x的取值范围是
。
的自变量x的取值范围是
。
7.写出一个图象经过点(1,一1)的函数解析式: .
8.已知一次函数![]() ,当
,当![]() =3时,
=3时,![]() =1,则b=__________
=1,则b=__________
9.已知点P(-2,3),则点P关于x轴对称的点坐标是( , )。
10.函数![]() 的图像如图所示,则y随
的图像如图所示,则y随 ![]() 的增大
的增大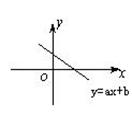 而 。
而 。
11.反比例函数 ![]() 的图像在
象限。
的图像在
象限。
12.函数![]() 中自变量x的取值范围是______________。
中自变量x的取值范围是______________。
13.当k = ________时,反比例函数![]() 的图象在第一象限.(只需填一个数)
的图象在第一象限.(只需填一个数)
14.函数y=![]() 中自变量x的取值范围是_____.
中自变量x的取值范围是_____.
15.若正比例函数y=mx (m≠0)和反比例函数y=![]() (n≠0)的图象都经过点(2,3),则
(n≠0)的图象都经过点(2,3),则
m =______, n =_________ .
三、解答题:
1、求下列函数中自变量x的取值范围:
(1)y=![]() ;
(2)y=x2-x-2;
;
(2)y=x2-x-2;
(3)y=![]() ;
(4)y=
;
(4)y=![]()
解:
(1)
(2)
(3)
(4)
2、分别写出下列各问题中的函数关系式及自变量的取值范围:
(1)某市民用电费标准为每度0.50元,求电费y(元)关于用电度数x的函数关系式;
(2)已知等腰三角形的面积为20cm2,设它的底边长为x(cm),求底边上的高y(cm)关于x的函数关系式;
(3)在一个半径为10 cm的圆形纸片中剪去一个半径为r(cm)的同心圆,得到一个圆环.设圆环的面积为S(cm2),求S关于r的函数关系式.
3.已知弹簧的长度 y(厘米)在一定的限度内是所挂重物质量 x(千克)的一次函数.现已测得不挂重物时弹簧的长度是6厘米,挂4千克质量的重物时,弹簧的长度是7.2厘米。求这个一次函数的关系式。
分析 已知y与x的函数关系是一次函数,则解析式必是![]() 的形式,所以要求的就是 和b的值。而两个已知条件就是x和y的两组对应值,也就是当x= 时,y=6,即得到点( ,6);当x=4时,y=7.2,即得到点(4,7.2)。可以分别将两个点的坐标代入函数式,得到一个关于k,b的方程组,进而求得 和b的值。
的形式,所以要求的就是 和b的值。而两个已知条件就是x和y的两组对应值,也就是当x= 时,y=6,即得到点( ,6);当x=4时,y=7.2,即得到点(4,7.2)。可以分别将两个点的坐标代入函数式,得到一个关于k,b的方程组,进而求得 和b的值。
解 设所求函数的关系式是y=kx+b,根据题意,得

解这个方程组,得![]()
所以所求函数的关系式是 。
运用待定系数法求解下题
4.已知一次函数的图象如下图,写出它的关系式。
分析:由图可知直线经过两点( , )、( , )
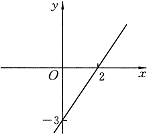 解:
解:
5、一次函数中,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,求出相应的函数关系式。
,求出相应的函数关系式。
解:设所求一次函数为 ,则依题意得
∴解方程组得![]() ∴所求一次函数为
∴所求一次函数为
6、已知一次函数y= kx+b的图象经过点(-1,1)和点(1,-5),求
(1)函数的解析式 (2)当x=5时,函数y的值。
四.综合题:(3分+2分+3分+4分)
已知一个二次函数的图象经过A(-2,![]() )、B(0,
)、B(0,![]() )和C(1,-2)三点。
)和C(1,-2)三点。
(1)求出这个二次函数的解析式;
(2)通过配方,求函数的顶点P的坐标;
(3)若函数的图象与x轴相交于点E、F,(E在F的左边),求出E、F两点的坐标。
(4)作出函数的图象并根据图象回答:当x取什么时,y>0,y<0,y=0
函数及图象答案
分层练习(A组)
一.选择题:C B C A C D A D B C C B C D A C C B C
二.填空题:
1.4 2. 三 3. –2![]() 4.y=(x-1)+2 5. y= -
4.y=(x-1)+2 5. y= - ![]() 6. x
6. x![]()
![]()
7. y=-x等 8.7 9. (-2,-3) 10. 减小 11. 二、四 13. -1等 14.x>![]() 且x
且x![]() 1
1
15. ![]() 6
6
三.解答题:
1.(1)一切实数 (2)一切实数 (3)x![]() 2 (4)x>-3
2 (4)x>-3
2. (1)y =0.5x
(x>0)
(2)y=![]() (3)s=100
(3)s=100![]() -
-![]() r
r![]() (0<r<10)
(0<r<10)
3.分析:kx+b k 0 0 k
解:![]()
![]() y=0.3x+6
y=0.3x+6
4.分析:(2,0) (0,-3)
解:y=kx+b ![]()
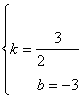
![]() y=
y=![]() x-3
x-3
5.解:y=kx+b
![]()
![]()
![]() y=-2x+5
y=-2x+5
5.(1)![]()
![]() y=-3x-2
y=-3x-2
(2) y=-17
四. ① y=0.5x2-x-1.5 ② y=0.5(x-1)2-2 p(1,-2)
③ E( -1,0 ) F(3,0) ④ 图略。当X<-1或X>3时y>0 .当-1<X<3时y<0
当X=-1,X=3时y=0