中等学校招生统一考试数学卷
数 学 试 题
| 题号 | 一 | 二 | 三 | 总分 |
| 得分 |
（总分100分，考试时间100分钟）
一、选择题（本大题有6个小题，每小题3分，共18分）
1.下列计算结果为负数的是（ ）
A、（－3）0 B、－｜－3｜ C、（－3）2 D、（－3）－2
2.如果代数式
有意义，那么直角坐标系中点P（m，n）的位置在（ ）
A、第一象限 B、第二象限 C、第三象限 D、第四象限
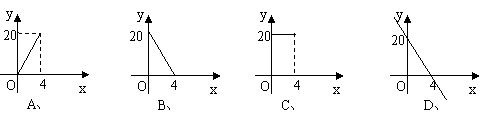
3.一根蜡烛长20cm，点燃后每小时燃烧5cm，燃烧时剩下的长度为y(cm)与燃烧时间x（小时）的函数关系用图象表示为下图中的（ ）
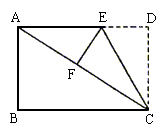
4.有一张矩形纸片ABCD，AB＝2.5，AD＝1.5，将纸片折叠，使AD边落在AB边上，折痕为AE，再将△AED以DE为折痕向右折叠，AC与BC交于点F（如下图），则CF的长为（ ）
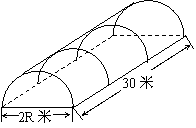
A、0.5 B、0.75 C、1 D、1.25
5.已知PA是⊙O的切线，A为切点，PBC是过点O的割线，PA＝10cm，PB＝5cm，则⊙O的半径长为（ ）
A、 15cm B、10 cm C、7.5 cm D、5 cm
6.参加保险公司的医疗保险，住院治疗的病人享受分段报销，保险公司制定的报销细则如下表.某人住院治疗后得到保险公司报销金额是1000元，那么此人住院的医疗费是（ ）
| 住院医疗费（元） | 报销率（%） |
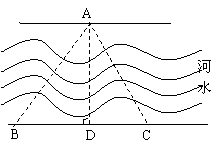
| 不超过500元的部分 | 0 |
| 超过500～1000元的部分 | 60 |
| 超过1000～3000元的部分 | 80 |
| …… |
A、1000元 B、1250元 C、1500元 D、2000元
二、真空题（本大题有8个小题，每小题3分，共24分，请将答案直接填写在题后的横线上）
7.在数轴上，与表示－1的点距离为3的点所表示的数是＿＿＿＿＿＿＿＿＿＿.
8. 函数y=中，自变量x的取值范围是 ；
9.某音像公司对外出租光盘的收费方法是：每张光盘出租后的前2天每天收费0.8元，以后每天收费0.5元，那么一张光盘在出租后第n天（n＞2且为整数）应收费＿＿＿＿＿元.
10、我国南方一些地区的农民戴的斗笠是圆锥形的母线长为30cm,底面圆的半径为24cm，则圆锥的侧面积为 cm2.（结果用π表示）
11. .按下列规律排列的一列数为：（2，1）、（5，4）、（8、7）…，则第5个数对中的两个数之和是 .
12.在平面直角坐标系中，入射光线经过y轴上点A（0，3），由x轴上点C反射，反射光线经过点B（－3，1），则点C的坐标为＿＿＿＿＿.
13.农村常需要搭建截面为半圆形的全封闭蔬菜塑料暖房（如图所示）则需塑料布y(m2)与半径R(m)的函数关系式是（不考虑塑料埋在土里的部分）＿＿＿＿＿＿＿＿＿.
14.已知直角三角形两边x、y的长满足｜x2－4｜＋
＝0，则第三边长为＿＿＿＿＿＿.
三、解答题（本大题有9个小题，共58分）
15.（本题满分5分）先化简(1+)÷，再选择一个恰当的x值代人并求值．
16.（本题满分5分）
已知关于x的一元二次方程
有两个不相等的实数根x1,x2
（1）求k的取值范围
（2）是否存在实数k，使
成立？，若存在，请求出k的值，若不存在，请说明理由。
17. （本题满分6分）
如图，在矩形ABCD中，AB＝6，BC＝8。将矩形ABCD沿CE折叠后，使点D恰好落在对角线AC上的点F处。
（1）求EF的长；
（2）求梯形ABCE的面积。
18.（本题满分6分）
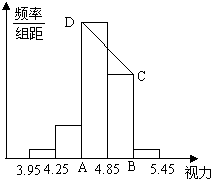青少年视力水平的下降已经引起全社会的关注，某校为了了解初中毕业年级500名学生的视力情况，从中抽查了一部分学生视力，通过数据处理，得到如下频率分布表和频率分布直方图：
| 分 组 | 频 数 | 频 率 |
| 3.95～4.25 | 2 | 0.04 |
| 4.25～4.55 | 6 | 0.12 |
| 4.55～4.85 | 25 | |
| 4.85～5.15 | ||
| 5.15～5.45 | 2 | 0.04 |
| 合 计 | 1.00 |
请你根据给出的图表回答：
⑴填写频率分布表中未完成部分的数据，
⑵在这个问题中，总体是＿＿＿＿＿＿＿＿＿＿＿＿，样本容量是＿＿＿＿＿＿＿.
⑶在频率分布直方图中梯形ABCD的面积是＿＿＿＿＿＿.
⑷请你用样本估计总体，可以得到哪些信息（写一条即可）＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿.
19.（本题满分6分）
为了测量汉江某段河面的宽度，秋实同学设计了如下图所示的测量方案：先在河的北岸选一定点A，再在河的南岸选定相距a米的两点B、C（如图），分别测得∠ABC＝α，∠ACB＝β，请你根据秋实同学测得的数据，计算出河宽AD.（结果用含a和含α、β的三角函数表示）
20.（本题满分6分）
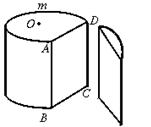
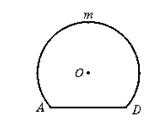
22．如图1，O为圆柱形木块底面的圆心，过底面的一条弦AD，沿母线AB剖开，得剖面矩形ABCD，AD＝24
cm，AB＝25 cm．若
的长为底面周长的
，如图2所示．
(1)求⊙O的半径；
(2)求这个圆柱形木块的表面积．(结果可保留p 和根号) 图1
21.（本题满分7分）
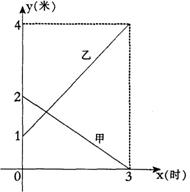
某企业有甲、乙两个长方体的蓄水池，将甲池中的水以每小时6立方米的速度注入乙池，甲、乙两个蓄水池中水的深度y(米)与注水时间x(时)之间的函数图象如图所示，结合图象回答下列问题：
(1)分别求出甲、乙两个蓄水池中水的深度y与注水时间x之间的函数关系式；
(2)求注水多长时间甲、乙两个蓄水池水的深度相同；
(3)求注水多长时间甲、乙两个蓄水池的蓄水量相同．
22、（本题满分8分）
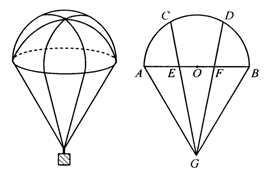
空投物资用的某种降落伞的轴截面如图所示，
是等边三角形，
、
是以
为直径的半圆
的两个三等分点，
、
分别交于点
、
，试判断点、分别位于所在线段的什么位置？并证明你的结论（证明一种情况即可）
23.（本题满分9分）
如图，直线
与
轴，
轴分别相交于点
，点，经过
两点的抛物线
与轴的另一交点为
，顶点为
，且对称轴是直线
．
（1）求点的坐标；
（2）求该抛物线的函数表达式；
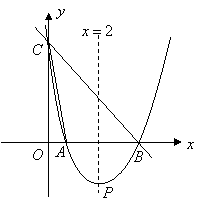（3）连结
．请问在轴上是否存在点
，使得以点
为顶点的三角形与
相似，若存在，请求出点的坐标；若不存在，请说明理由．