《三角形》提高测试
一 判断题（本题10分，每小题2分）
１．三角形三条高的交点不在三角形内就在三角形外…………………………………（ ）
２．如果一个三角形的周长为35cm，且其中两边都等于第三边的2倍，那么这个三角形的最短边为7……………………………………………………………………………（ ）
３．一个三角形的一个外角小于和它相邻的一个内角，那么这个三角形是钝角三角形………………………………………………………………………………………（ ）
４．三角形的外角中，至少有1个是钝角………………………………………………（ ）
５．三条线段a，b，c中，a＝5，b＝3，c的长是整数，以a，b，c为边组成三角形的个数共有5个…………………（ ）答案：１．×；２．√；３．√；４．×；５．√．
二 填空题（本题20分，每小题4分）：
１．△ABC中，∠A＝2∠B，∠C＝∠A＋∠B＋12°，则∠A＝ ，∠B＝ ，∠C＝ ；
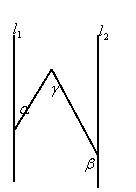
２．如图1，l1∥l2， ∠
＝142°，∠
＝73°，则∠
＝ ；
３．直角三角形两锐角的平分线所夹的钝角的度数为 ；
４．△ABC中，∠A∶∠B∶∠C＝1∶2∶3，AB＝10，则BC＝ ；
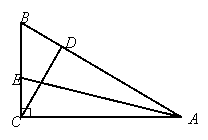
５．如图2，△ABC中，∠ACB＝90°，CD⊥AB于D，∠CAD＝40°，∠CEA＝70°，则∠EAB＝ .
图1 图2答案：１．56°，28°，96°；
２．35°；３．135°；４．5；５．20°．
三 选择题（本题20分，每小题5分）：
１．在下列四个结论中，正确的是……………………………………………………（ ）
（A）三角形的三个内角中最多有一个锐角（B）等腰三角形的底角一定大于顶角
（C）钝角三角形最多有一个锐角（D）三角形的三条内角平分线都在三角形内
２．四条线段的长度分别为4、6、8、10，可以组成三角形的组数为……………（ ）
（A）4 （B）3 （C）2 （D）1
３．在△ABC中，AB＝AC，D、E分别是AB、AC的中点，BE、CD交于G，AG的延长线交BC于F，那么图中全等三角形的对数是……………………………………………（ ）
（A）4对 （B）5对 （C）6对 （D）7对
４．如图4，∠B＝60°，∠C＝40°，∠BDC＝3∠A，则∠A的度数为…………（ ）
（A）80° （B）30° （C）50° （D）无法确定
５．如图5，AE与BF交于C，且AB＝AC，CE＝CF．∠E＝．那么，∠A用可以表示成…………………………………（ ）
（A）180°－ （B）180°－ 4 （C）2－180° （D）4－180°
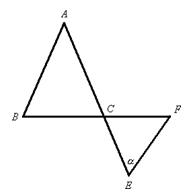
图3 图4
答案：１．Ｄ；２．Ｂ；３．Ｄ；４．Ｃ；５．Ｄ．
四 （本题10分）
如图，等腰直角三角形ABC中，∠ACB＝90°，AD为腰CB上的中线，CE⊥AD交AB于E．求证∠CDA＝∠EDB．
提示：
作CF⊥AB于F，则∠ACF＝45°，
在△ABC中，∠ACB＝90°，CE⊥AD，
于是，由∠ACG＝∠B＝45°，AB＝AC ，
且易证∠1＝∠2，
由此得△AGC≌△CEB（ASA）．
再由CD＝DB，CG＝BE，∠GCD＝∠B，
又可得△CGD≌△BED（SAS），
则可证∠CDA＝∠EDB．
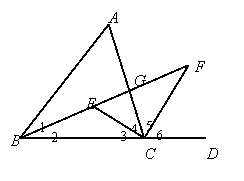
五 如图，△ABC中，∠1＝∠2，∠3＝∠4，∠5＝∠6．∠A＝60°．求∠ECF、∠FEC的度数．
略解：因为 ∠A＝60°，
所以 ∠2＋∠3＝
（180°－60°）＝60°；
又因为 B、C、D是直线，
所以 ∠4＋∠5＝90°；
于是 ∠FEC＝∠2＋∠3＝60°，
∠FCE＝∠4＋∠5＝90°，
∠FEC＝60°．
六 在Rt△ABC中，∠A＝90°，CE是角平分线，和高AD相交于F，作FG∥BC交AB于G，求证：AE＝BG．
略解：作EH⊥BC于H，
由于E是角平分线上的点，可证 AE＝EH ；
且又由 ∠AEC＝∠B＋∠ECB＝∠CAD＋∠ECA＝∠AFE
可证 AE＝AF，
于是由 AF＝EH，∠AFG＝∠EHB＝90°，∠B＝∠AGF．
可得 △AFG≌△EHB；
所以 AG＝EB，
即 AE＋EG＝BG＋GE，
所以 AE＝BG．