中考数学模拟试题41
班级：_________ 姓名：_________ 得分：_________
一、填空题(每小题3分，共24分)
1．如果a＋a＝0，则
＋
＝______．
2．已知x2-x-1＝0，则代数式-x3＋2x2＋2002的值为______．
3．若由你选择一个你喜欢的数值m，使一次函数y＝(m-2)x＋m的图象经过第一、二、四象限，则m的值可以是______．
4．升国旗时，某同学站在离旗杆底部18米处行注目礼，当国旗升至旗杆顶端时，该同学视线的仰角恰为45°，若该同学双眼离地面1.6米，则旗杆高度为______米．
5．如图1，某涵洞的截面是抛物线形，现测得水面宽AB＝1.6 m，涵洞顶点O到水面的距离CO为2.4 m，在图中直角坐标系内，涵洞截面所在抛物线的解析式是______．
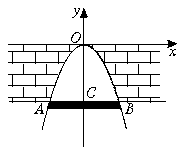
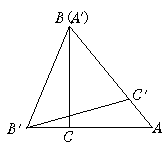
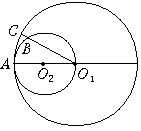
图1 图2 图3
6．已知一个圆的弦切角等于40°，那么这个弦切角所夹的弧所对的圆心角的度数是______．
7．如图2，在Rt△ABC中，腰AC＝BC＝1，按下列方法折叠Rt△ABC，点B不动，使BC落在AB上，点A不动，使AB落在AC的延长线上；点C不动，使CA落在CB上，设点A、B、C对应的落点分别为A′、B′、C′，则△A′B′C′的面积是______．
8．如图3，⊙O1的半径是⊙O2的直径，⊙O1的半径O1C交⊙O2于B，若
的度数是48°，那么
的度数是______．
二、选择题(每小题3分，共18分)
9．如果一个多边形的内角和等于它的外角和的2倍，那么这个多边形的边数为( )
A．3 B．4 C．5 D．6
10．在一次汽车性能测试中，型号不同的甲、乙两辆汽车同时从A地出发，匀速向距离560千米的B地行驶，结果甲车7小时到达，乙车8小时到达，则两车行驶时离A地的距离s(千米)与行驶时间t(小时)的函数关系对应的图象大致是( )
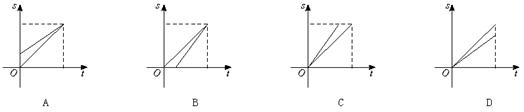
11．两圆的圆心坐标分别为(3，0)，(0，4)，它们的直径分别为4和6，则这两圆的位置关系是( )
A．外离 B．相交 C．外切 D．内切
12．在Rt△ABC中，∠C＝Rt，若∠A＝30°，则cosA＋sinB等于( )
A．
B．1 C．
D．
13．在直角坐标系中，已知A(1，1)，在x轴上确定点P，使△AOP为等腰三角形，则符合条件的点P共有( )
A．1个 B．2个 C．3个 D．4个
14．当今材料科学已发展到纳米时代，1纳米等于1米的十亿分之一，我国科学家已研制成功直径为0.4纳米的碳米管，如果用科学记数法表示这种碳米管的直径，应为( )
A．4×10-9米 B．0.4×10-8米 C．4×10-10米 D．0.4×10-9米
三、解答题(15～19每小题8分，共40分)
15．解方程
．
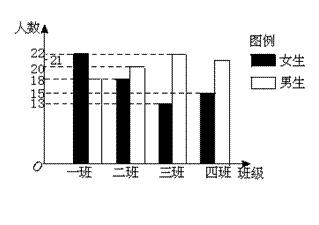
16．某校初二年级四个班的同学外出植树一天，已知每小时5个女生种3棵树，3个男生种5棵树，各班人数如图所示，则植树最多的是初二几班．
17．声音在空气中传播的速度y(米/秒)(简称音速)与气温x(℃)有关，下表列出了一组不同气温时的音速：
| 气温x(℃) | 0 | 5 | 10 | 15 | 20 |
| 音速y(米/秒) | 331 | 334 | 337 | 340 | 343 |
(1)求y与x之间的函数关系式；
(2)当气温为22°时，某人看到烟花燃放5秒后才听到声响，那么此人与燃放的烟花所在地约相距多少米？
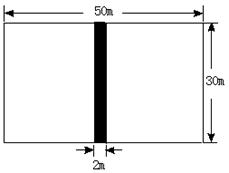
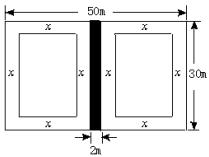
18．某广场有一块长50米、宽30米的空地，现要将它改造为花园，请你设计一个修建方案，使满足下列条件：
(1)正中间留出一条宽2米的道路(如图)；
(2)道路两旁修建花坛，且花坛总面积占整个面积(不包括道路)的一半；
(3)设计好的整个图形既是轴对称图形，又是中心对称图形．(计算结果精确到0.1米)．
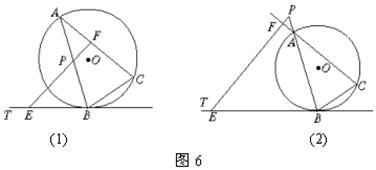
19．已知：△ABC是⊙O的内接三角形，BT为⊙O的切线，B为切点，P为直线AB上一点，过P作BC的平行线交直线BT于点E，交直线AC于点F．
(1)如图6(1)所示，当P在线段AB上时，求证：PA·PB＝PE·PF；
(2)如图6(2)所示，当P为线段BA延长线上一点时，第(1)题的结论还成立吗？如果成立，请给出证明；如果不成立，请说明理由．
四、解答题(每题9分，共18分)
20．先仔细阅读下列材料，然后回答问题：
如果a＞0，b＞0，那么(
-
)2≥0，即a＋b-2
≥0 得
≥2
其中，当a＝b时取等号，我们把称为a、b的算术平均数， 称为a、b的几何平均数．
如果a＞0，b＞0，c＞0，同样可以得到
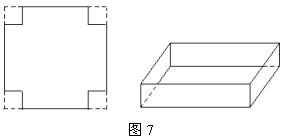
≥3
，其中，当a＝b＝c时取等号于是就有定理：几个正数的算术平均数不小于它们的几何平均数．请用上述定理解答问题：把边长为30 cm的正方形纸片的4角各剪去一个小正方形，折成无盖纸盒(如图7)
(1)设剪去的小正方形边长为x cm，无盖纸盒的容积为V，求V与x的函数关系式及x的取值范围．
(2)当x为何值时，容积V有最大值，最大值是多少？
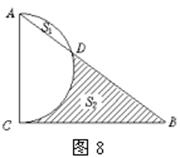
21．以△ABC的边AC为直径的半圆交AB边于D点，∠A、∠B、∠C所对边长为a、b、c，且二次函数y＝
(a＋c)x2-bx＋(c-a)顶点在x轴上，a是方程z2＋z-20＝0的根．
(1)证明：∠ACB＝90°；
(2)若设b＝2x，弓形面积S弓形AED＝S1，阴影面积为S2，求(S2-S1)与x的函数关系式；
(3)在(2)的条件下，当BD为何值时，(S2-S1)最大？
参考答案
一、1．-2a＋1 2．2003 3．1(满足0＜m＜2的m值均可
4．19.6 5．y＝-
x2 6．80°
7．S△A′B′C′＝S△ABB′-S△AB′C′＝AB·AB′sinA-AC′·AB′sinA
＝AB′·(AB-AC′)sinA＝
［
-(-1)］sin45°＝
8．24°
二、9．D 10．C 11．C 12．C 13．D 14．C
三、15．x1＝-1，x2＝3．
16．由图可知
| 一班 | 二班 | 三班 | 四班 | |
| 女生数(人) | 22 | 18 | 13 | 15 |
| 男生数(人) | 18 | 20 | 22 | 21 |
因为每班男、女生种树的速度相同，所以每班人数减去相同的女生数和男生数，比较结果不变，每个班减去13个女生和18个男生，一班余下女生9人，可植树
×9＝5
(棵)．二班余下女生5人和男生2人，可植树×5＋
×2＝6
(棵)．三班余下男生4人，可植树×4＝6
(棵)．四班余下女生2人和男生3人，可植树×2＋×3＝6
(棵)．所以种树最多的班级是三班．
17．解：(1)依题可设，y＝kx＋b，则有
解得
∴ y＝x＋331．
(2)当x＝22时，y＝×22＋331＝344.2
334.2×5＝1721．
∴ 此人与燃放的烟花所在地约相距1721米．
18．这里给出一种设计方案(如图)．下面求出x即可．根据
题意可列方程：(50-2-4x)(30-2x)＝
．
x的值约取3.9米．
这里只给出了一种设计方案，仅供参考．
19．(1)由△APF∽△EPB，
，
∴ PA·PB＝PE·PF．
(2)结论成立，证法同上(略)．
四、20．(1)V＝x(30-2x)(30-2x)＝4x(15-x)2(0＜x＜15)
(2)V＝2·2x·(15-x)·(15-x)≤2·［
］3＝2×103
这时，当2x＝15-x，即x＝5时取等号．
∴ 当剪去的小正方形边长为5 cm时，无盖空盒的容积最大为2×103 cm3
21．(1)因为二次函数y＝(a＋c)x2-bx＋(c-a)的顶点在x轴上，
∴ Δ＝0，即：b2-4×(a＋c)×(c-a)＝0，
∴ c2＝a2＋b2，得∠ACB＝90°．
或者从抛物线顶点的纵坐标为零求得：
即y＝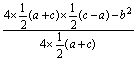
＝0
可得c2＝a2＋b2．
(2)∵ z2＋z-20＝0．
∴ z1＝-5，z2＝4，
∵ a＞0，得a＝4．
设b＝AC＝2x，有S△ABC＝AC·BC＝4x，S半圆＝p x2
∴ S2-S1＝S△ABC-(S半圆-S1)-S1＝S△ABC-S半圆＝-
x2＋4x
(3)S2-S1＝-(x-
)2＋
，
∴ 当x＝时，(S2-S1)有最大值．
这时，b＝，a＝4，c＝
BD＝
．