中考复习系列《图形的认识》
第二课时 三角形
初三（ ）班 学号： 姓名：
一、中考知识要点
1、三角形基本概念
（1）三边关系：
三角形任意两边之和 第三边，三角形任意两边之差 第三边。
（2）三角形内角和定理：三角形的三个内角和等于 。
（3）外角性质：三角形的一个外角等于和它 的两内角的和。
三角形的一个外角大于任何一个和它 的内角。（填“不相邻”或“相邻”）
（4）角平分线：OC是
，则∠ =∠ =
∠
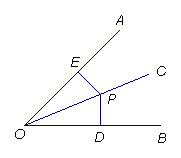角平分线定理：角平分线上的点到 的两边的距离
。
OC是，P是OC上一点，
PE
，则
=
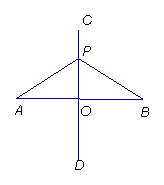（5）线段垂直平分线定理：
线段垂直平分线上的点到这条线段 的距离 。
直线CD是线段AB的垂直平分线，P是CD上一点，
O是垂足，则 = ， =
（6）三角形的三条角平分线相交于一点（ 心）；
三条边的垂直平分线相交于一点（ 心）。
（7）中位线：三角形的中位线 第三边，并且等于 。
2、特殊的三角形
等腰三角形
（1）等腰三角形的两个底角 ，简写成：等边对 。
（2）等腰三角形的顶角 、底边上的 、底边上的高 。
（3）如果一个三角形有两个角相等，那么这两个角所对的 也相等，
简写成：等角对 。
如果一个三角形有两条边相等，那么这两条边所对的 也相等，
简写成：等边对 。
（4）三个角相等的三角形是 三角形。
（5）有一个角等于60°的等腰三角形是 三角形。
直角三角形
（1）直角三角形两锐角 。
（2）在直角三角形中，30°角所对的直角边等于斜边的 。
（3）勾股定理：
在Rt
ABC中，
AB=a, BC=b, AC=c，则a，b，c满足关系：
a= ，b= ，c=
在RtABC中，AB=5，BC=4，则AC= .
在RtABC中，
AB=4，BC=3，则AC= .
在RtABC中，AB=1，AC=2，则BC= .
（4）勾股定理逆定理：如果三角形三边为a，b，c，满足
，那么这个三角形为直角三角形。
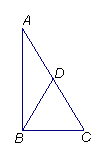
（5）直角三角形斜边上的中线等于 。
在RtABC中, D是AC边的中点，
已知AC=4,则BD=
3、相似三角形
（1）相似三角形的性质
相似三角形的对应边 ，对应角 。
对应高的比、对应角平分线的比、对应中线的比、对应周长的比都等于 比。
对应面积的比等于 。
（2）相似三角形的识别方法：
①如果两个三角形 角对应 ，那么这两个三角形相似。
②如果两个三角形 边对应 ，那么这两个三角形相似。
③如果两个三角形 边对应 ，且 ，那么这两个三角形相似。
4、全等三角形
全等三角形对应边 ，对应角 ；对应边、对应中线、对应高、对应角平分线 ； 全等三角形的周长、面积 。
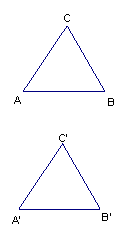
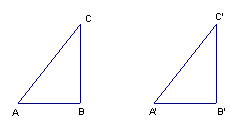
一般三角形全等的判定（如图）
(1) 边角边（SSS）
∵AB=A′B′ BC=B′C ′ _______=_____∴△ABC≌△A′B′C′
（2）边角边（SAS）
∵AB=A′B′ ∠B=∠B′ _______=_____
∴△ABC≌△A′B′C′
(3) 角边角（ASA）
∠B=∠B′ ____=_____ ∠C=∠C′ ∴△ABC≌△A′B′C′
(4) 角角边（AAS）
∵∠A=∠A′ ∠C=∠C′ _______=_____
∴△ABC≌△A′B′C′
直角三角形全等的判定：
斜边直角边定理（ ）
AB=A′B′ _____=_____
∴Rt△ABC≌Rt△A′B′C′
5、三角形的面积
（1）一般三角形：S= (h是a边上的高)
（2）直角三角形：S= = (a,b是直角边，c是斜边，h是斜边上的高)
（3）等边三角形：S= (a是边长)
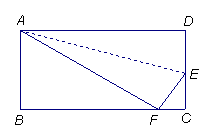
例1、 折叠长方形的一边AD，使点D落在BC边上的点F处，已知AB=8cm,
BC=10cm,求CE的长。
分析：AFE是ADE翻折得到的，则AFE
ADE
 |
习题1、如果ABC∽
，相似比k=1∶2,
ABC与的周长比为
；ABC与的对应高线比为 ；
ABC与的对应边的中线比为
；
与ABC的对应角的角平分线比为
；
ABC与的面积比为 。
2、、下列条件中，能判定△ABC≌△DEF的是（ ）
A AB=DE,BC=EF, ∠A=∠D B ∠A=∠D, ∠C=∠F,AC=EF
C ∠B=∠E,∠A=∠D,AC=EF D AB=DE,BC=EF, △ABC的周长等于△DEF的周长
3、能判定两个三角形全等的是（ ）
A ∠A=∠A′,∠B=∠B′,∠C=∠C′ B BC=B′C′,AC=A′C′,∠B=∠B′
C AC=A′C′,∠A=∠A′,∠B=∠B′ D ∠A=∠A′,∠B=∠C′,AC=A′C′
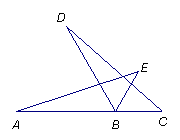
4、如图，AB=DB,BC=BE，要使△AEB≌△DCB,
则需增加的条件是（ ）
A ∠A＝∠D B ∠E＝∠C
C ∠A＝∠C D ∠ABE＝∠DBC
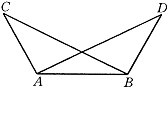
1.如图，AC＝BD，BC＝AD，说明△ABC和△BAD全等的理由．
 |
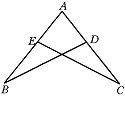2、如图，∠BDA＝∠CEA，AE＝AD．求证：AB＝AC．
3.如图，∠1＝∠2，∠B＝∠D，△ABC和△ADC全等吗？
 |
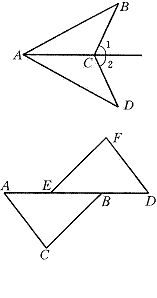4、如图，AB＝DE，AC∥DF，BC∥EF，△ABC与△DEF全等吗？
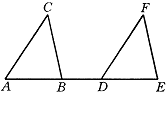
5、如图，AE＝DB，BC＝EF，BC∥EF，说明△ABC和△DEF全等的理由．
 |
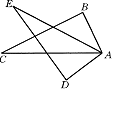6、如图，AB＝AD，AC＝AE，∠BAE＝∠DAC，
△ ABC与△ADE全等吗？
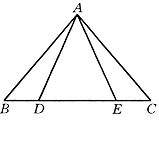7、如图，已知AB＝AC，BD＝CE，说明△ABD≌△ACE.
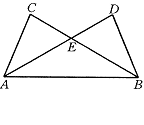
8、如图，∠C＝∠D，CE＝DE．求证：∠DAB＝∠ABC．
 |
9、已知：如图，D是△ABC的边BC的中点，∠BAC=90°，延长AD至E，使DE=AD，连BE，求证：△ABE≌△BAC