中考数学二次函数分类汇编试题含答案
一、选择题
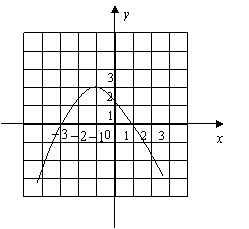
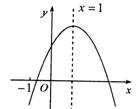 1、(2007天津市)已知二次函数
1、(2007天津市)已知二次函数![]() 的图象如图所示,有下列5个结论:①
的图象如图所示,有下列5个结论:① ![]() ;②
;② ![]() ;③
;③ ![]() ;④
;④ ![]() ;⑤
;⑤ ![]() ,(
,(![]() 的实数)其中正确的结论有(
)B
的实数)其中正确的结论有(
)B
 A. 2个 B.
3个 C.
4个 D.
5个
A. 2个 B.
3个 C.
4个 D.
5个
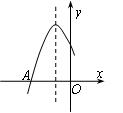
2、(2007南充)如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为x=-1.给出四个结论:①b2>4ac;②2a+b=0;③a-b+c=0;④5a<b.其中正确结论是( ).B
(A)②④ (B)①④ (C)②③ (D)①③
3、(2007广州市)二次函数![]() 与x轴的交点个数是( )B
与x轴的交点个数是( )B
A.0 B.1 C.2 D.3
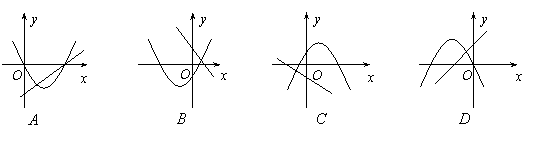
4、(2007云南双柏县)在同一坐标系中一次函数![]() 和二次函数
和二次函数
![]() 的图象可能为( )A
的图象可能为( )A
 |
5、(2007四川资阳)已知二次函数![]() (a≠0)的图象开口向上,并经过点(-1,2),(1,0) . 下列结论正确的是( )D
(a≠0)的图象开口向上,并经过点(-1,2),(1,0) . 下列结论正确的是( )D
A. 当x>0时,函数值y随x的增大而增大
B. 当x>0时,函数值y随x的增大而减小
C. 存在一个负数x0,使得当x<x0时,函数值y随x的增大而减小;当x> x0时,函数值y随x的增大而增大
D. 存在一个正数x0,使得当x<x0时,函数值y随x的增大而减小;当x>x0时,函数值y随x的增大而增大
6、(2007山东日照)已知二次函数y=x2-x+a(a>0),当自变量x取m时,其相应的函数值小于0,那么下列结论中正确的是( )B
(A) m-1的函数值小于0 (B) m-1的函数值大于0
(C) m-1的函数值等于0 (D) m-1的函数值与0的大小关系不确定
 二、填空题
二、填空题
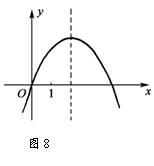
1、(2007湖北孝感)二次函数y =ax2+bx+c 的图象如图8所示,
且P= a-b+c + 2a+b ,Q= a+b+c + 2a-b ,
则P、Q的大小关系为 . P<Q
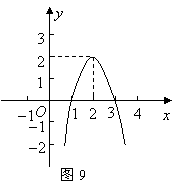
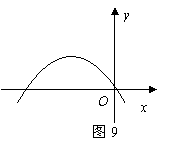 2、(2007四川成都)如图9所示的抛物线是二次函数
2、(2007四川成都)如图9所示的抛物线是二次函数![]() 的图象,那么
的图象,那么![]() 的值是 .-1
的值是 .-1
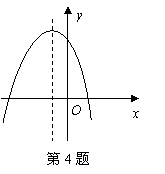
 3、(2007江西省)已知二次函数
3、(2007江西省)已知二次函数![]() 的部分图象如图所示,则关于
的部分图象如图所示,则关于![]() 的一元二次方程
的一元二次方程![]() 的解为
.
的解为
.
![]() ,
,![]() ;
;
4、(2007广西南宁)已知二次函数![]() 的图象如图所示,则点
的图象如图所示,则点![]() 在第
象限. 三
在第
象限. 三
三、解答题
1、(2007天津市)知一抛物线与x轴的交点是![]() 、B(1,0),且经过点C(2,8)。
、B(1,0),且经过点C(2,8)。
(1)求该抛物线的解析式;
(2)求该抛物线的顶点坐标。
解:(1)设这个抛物线的解析式为![]()
由已知,抛物线过![]() ,B(1,0),C(2,8)三点,得
,B(1,0),C(2,8)三点,得
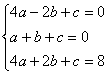 (3分)解这个方程组,得
(3分)解这个方程组,得![]()
∴ 所求抛物线的解析式为![]() (6分)
(6分)
(2)![]()
∴ 该抛物线的顶点坐标为![]()
2、(2007上海市)在直角坐标平面内,二次函数图象的顶点为![]() ,且过点
,且过点![]() .
.
(1)求该二次函数的解析式;
(2)将该二次函数图象向右平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与![]() 轴的另一个交点的坐标.
轴的另一个交点的坐标.
解:(1)设二次函数解析式为![]() ,
,
![]() 二次函数图象过点
二次函数图象过点![]() ,
,![]() ,得
,得![]() .
.
![]() 二次函数解析式为
二次函数解析式为![]() ,即
,即![]() .
.
(2)令![]() ,得
,得![]() ,解方程,得
,解方程,得![]() ,
,![]() .
.
![]() 二次函数图象与
二次函数图象与![]() 轴的两个交点坐标分别为
轴的两个交点坐标分别为![]() 和
和![]() .
.
![]() 二次函数图象向右平移1个单位后经过坐标原点.
二次函数图象向右平移1个单位后经过坐标原点.
平移后所得图象与![]() 轴的另一个交点坐标为
轴的另一个交点坐标为![]()
 3、(2007广东梅州)已知二次函数图象的顶点是
3、(2007广东梅州)已知二次函数图象的顶点是![]() ,且过点
,且过点![]() .
.
(1)求二次函数的表达式,并在图10中画出它的图象;
(2)求证:对任意实数![]() ,点
,点![]() 都不在这个
都不在这个
二次函数的图象上.
解:(1)依题意可设此二次函数的表达式为![]() ,··································· 2分
,··································· 2分
又点![]() 在它的图象上,可得
在它的图象上,可得![]() ,解得
,解得![]() .
.
 所求为
所求为![]() . 令
. 令![]() ,得
,得![]()
画出其图象如右.
(2)证明:若点![]() 在此二次函数的图象上,
在此二次函数的图象上,
则![]() . 得
. 得![]() .
.
方程的判别式:![]() ,该方程无解.
,该方程无解.
所以原结论成立.
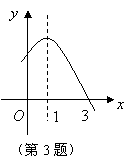
 4、(2007贵州省贵阳)二次函数
4、(2007贵州省贵阳)二次函数![]() 的图象如图9所示,根据图象解答下列问题:
的图象如图9所示,根据图象解答下列问题:
(1)写出方程![]() 的两个根.(2分)
的两个根.(2分)
(2)写出不等式![]() 的解集.(2分)
的解集.(2分)
(3)写出![]() 随
随![]() 的增大而减小的自变量
的增大而减小的自变量![]() 的取值范围.(2分)
的取值范围.(2分)
(4)若方程![]() 有两个不相等的实数根,求
有两个不相等的实数根,求![]() 的取值范围.(4分)
的取值范围.(4分)
解:(1)![]() ,
,![]()
(2)![]()
(3)![]()
(4)![]()
 5、(2007河北省)如图13,已知二次函数
5、(2007河北省)如图13,已知二次函数![]() 的图像经过点A和点B.
的图像经过点A和点B.
(1)求该二次函数的表达式;
(2)写出该抛物线的对称轴及顶点坐标;
(3)点P(m,m)与点Q均在该函数图像上(其中m>0),且这两点关于抛物线的对称轴对称,求m的值及点Q 到x轴的距离.
解:(1)将x=-1,y=-1;x=3,y=-9分别代入![]() 得
得
![]() 解得
解得 ![]() ∴二次函数的表达式为
∴二次函数的表达式为![]() .
.
(2)对称轴为![]() ;顶点坐标为(2,-10).
;顶点坐标为(2,-10).
(3)将(m,m)代入![]() ,得
,得 ![]() ,
,
解得![]() .∵m>0,∴
.∵m>0,∴![]() 不合题意,舍去.
不合题意,舍去.
∴ m=6.∵点P与点Q关于对称轴![]() 对称,∴点Q到x轴的距离为6.
对称,∴点Q到x轴的距离为6.
6、(2007四川成都)在平面直角坐标系![]() 中,已知二次函数
中,已知二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左边),与
的左边),与![]() 轴交于点
轴交于点![]() ,其顶点的横坐标为1,且过点
,其顶点的横坐标为1,且过点![]() 和
和![]() .
.
(1)求此二次函数的表达式;
(2)若直线![]() 与线段
与线段![]() 交于点
交于点![]() (不与点
(不与点![]() 重合),则是否存在这样的直线
重合),则是否存在这样的直线![]() ,使得以
,使得以![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,求出该直线的函数表达式及点
相似?若存在,求出该直线的函数表达式及点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
 (3)若点
(3)若点![]() 是位于该二次函数对称轴右边图象上不与顶点重合的任意一点,试比较锐角
是位于该二次函数对称轴右边图象上不与顶点重合的任意一点,试比较锐角![]() 与
与![]() 的大小(不必证明),并写出此时点
的大小(不必证明),并写出此时点![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
解:(1)![]() 二次函数图象顶点的横坐标为1,且过点
二次函数图象顶点的横坐标为1,且过点![]() 和
和![]() ,
,
![]() 由
由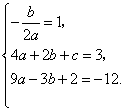 解得
解得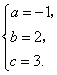
![]() 此二次函数的表达式为
此二次函数的表达式为 ![]() .
.
(2)假设存在直线![]() 与线段
与线段![]() 交于点
交于点![]() (不与点
(不与点![]() 重合),使得以
重合),使得以![]() 为顶点的三角形与
为顶点的三角形与![]() 相似.
相似.
在![]() 中,令
中,令![]() ,则由
,则由![]() ,解得
,解得![]()
![]() .
.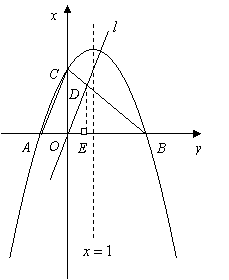 令
令![]() ,得
,得![]() .
.![]() .
.
设过点![]() 的直线
的直线![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() .
.
![]() 点
点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
![]()
![]() .
.
要使![]() 或
或![]() ,
,
已有![]() ,则只需
,则只需![]() , ①
, ①
或![]() ② 成立.
② 成立.
若是①,则有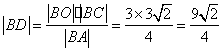 .而
.而![]() .
.
![]() 在
在![]() 中,由勾股定理,得
中,由勾股定理,得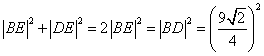 .
.
解得 ![]() (负值舍去).
(负值舍去).![]() .
.
![]() 点
点![]() 的坐标为
的坐标为![]() .将点
.将点![]() 的坐标代入
的坐标代入![]() 中,求得
中,求得![]() .
.
![]() 满足条件的直线
满足条件的直线![]() 的函数表达式为
的函数表达式为![]() .
.
[或求出直线![]() 的函数表达式为
的函数表达式为![]() ,则与直线
,则与直线![]() 平行的直线
平行的直线![]() 的函数表达式为
的函数表达式为![]() .此时易知
.此时易知![]() ,再求出直线
,再求出直线![]() 的函数表达式为
的函数表达式为![]() .联立
.联立![]() 求得点
求得点![]() 的坐标为
的坐标为![]() .]
.]
若是②,则有![]() .而
.而![]() .
.
![]() 在
在![]() 中,由勾股定理,得
中,由勾股定理,得![]() .
.
解得 ![]() (负值舍去).
(负值舍去).![]() .
.![]() 点
点![]() 的坐标为
的坐标为![]() .
.
将点![]() 的坐标代入
的坐标代入![]() 中,求得
中,求得![]() .
.![]() 满足条件的直线
满足条件的直线![]() 的函数表达式为
的函数表达式为![]() .
.
![]() 存在直线
存在直线![]() 或
或![]() 与线段
与线段![]() 交于点
交于点![]() (不与点
(不与点![]() 重合),使得以
重合),使得以![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,且点
相似,且点![]() 的坐标分别为
的坐标分别为![]() 或
或![]() .
.
(3)设过点![]() 的直线
的直线![]() 与该二次函数的图象交于点
与该二次函数的图象交于点![]() .
.
将点![]() 的坐标代入
的坐标代入![]() 中,求得
中,求得![]() .
.![]() 此直线的函数表达式为
此直线的函数表达式为![]() .
.
 设点
设点![]() 的坐标为
的坐标为![]() ,并代入
,并代入![]() ,得
,得![]() .
.
解得![]() (不合题意,舍去).
(不合题意,舍去).![]() .
.
![]() 点
点![]() 的坐标为
的坐标为![]() .此时,锐角
.此时,锐角![]() .
.
又![]() 二次函数的对称轴为
二次函数的对称轴为![]() ,
,
![]() 点
点![]() 关于对称轴对称的点
关于对称轴对称的点![]() 的坐标为
的坐标为![]() .
.
![]() 当
当![]() 时,锐角
时,锐角![]() ;当
;当![]() 时,锐角
时,锐角![]() ;
;
当![]() 时,锐角
时,锐角![]() .
.
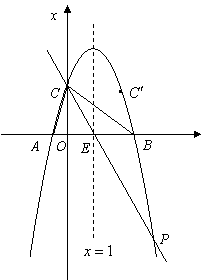
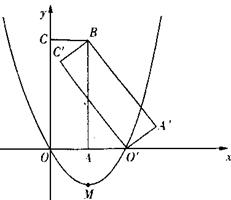
7、(2007四川眉山)如图,矩形A’BC’O’是矩形OABC(边OA在x轴正半轴上,边OC在y轴正半轴上)绕B点逆时针旋转得到的.O’点在x轴的正半轴上,B点的坐标为(1,3).
(1)如果二次函数y=ax2+bx+c(a≠0)的图象经过O、O’两点且图象顶点M的纵坐标为
—1.求这个二次函数的解析式;
(2)在(1)中求出的二次函数图象对称轴的右支上是否存在点P,使得ΔPOM为直角三角形?若存在,请求出P点的坐标和ΔPOM的面积;若不存在,请说明理由;
(3)求边C’O’所在直线的解析式.
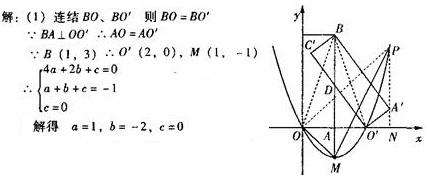

8、(2007山东日照)容积率t是指在房地产开发中建筑面积与用地面积之比,即t=![]() ,为充分利用土地资源,更好地解决人们的住房需求,并适当的控制建筑物的高度,一般地容积率t不小于1且不大于8.一房地产开发商在开发某小区时,结合往年开发经验知,建筑面积M(m2)与容积率t的关系可近似地用如图(1)中的线段l来表示;1 m2建筑面积上的资金投入Q(万元)与容积率t的关系可近似地用如图(2)中的一段抛物线段c来表示.
,为充分利用土地资源,更好地解决人们的住房需求,并适当的控制建筑物的高度,一般地容积率t不小于1且不大于8.一房地产开发商在开发某小区时,结合往年开发经验知,建筑面积M(m2)与容积率t的关系可近似地用如图(1)中的线段l来表示;1 m2建筑面积上的资金投入Q(万元)与容积率t的关系可近似地用如图(2)中的一段抛物线段c来表示.
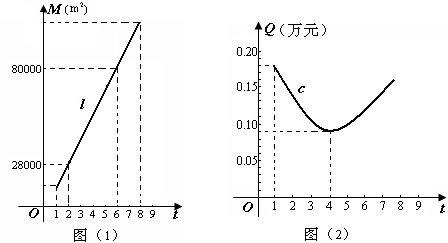 |
(Ⅰ)试求图(1)中线段l的函数关系式,并求出开发该小区的用地面积;
(Ⅱ)求出图(2)中抛物线段c的函数关系式.
解:(Ⅰ)设线段l函数关系式为M=kt+b,由图象得
![]() 解之,得
解之,得![]()
∴线段l的函数关系式为M=13000t+2000, 1≤t≤8.
由t=![]() 知,当t=1时,S用地面积=M建筑面积,
知,当t=1时,S用地面积=M建筑面积,
把t=1代入M=13000t+2000中,得M=15000 m2.
即开发该小区的用地面积是15000 m2.
(Ⅱ)根据图象特征可设抛物线段c的函数关系式为Q=a( t-4)2+k, 把点(4,0.09), (1,0.18)代入,得![]()
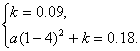 解之,得
解之,得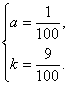
∴抛物线段c的函数关系式为 Q=![]() ( t-4)2+
( t-4)2+![]() ,即Q=
,即Q=![]() t2-
t2-![]() t +
t +![]() , 1≤t≤8.
, 1≤t≤8.
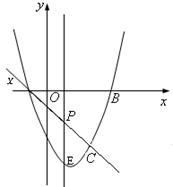
9、(2006四川资阳)如图10,已知抛物线P:y=ax2+bx+c(a≠0) 与x轴交于A、B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F、G分别在线段BC、AC上,抛物线P上部分点的横坐标对应的纵坐标如下:
| x | … | -3 | -2 | 1 | 2 | … |
| y | … | - | -4 | - | 0 | … |
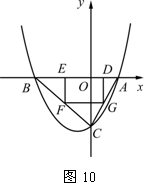 (1) 求A、B、C三点的坐标;
(1) 求A、B、C三点的坐标;
(2) 若点D的坐标为(m,0),矩形DEFG的面积为S,求S与m的函数关系,并指出m的取值范围;
(3) 当矩形DEFG的面积S取最大值时,连接DF并延长至点M,使FM=k·DF,若点M不在抛物线P上,求k的取值范围.
若因为时间不够等方面的原因,经过探索、思考仍无法圆满解答本题,请不要轻易放弃,试试将上述(2)、(3)小题换为下列问题解答(已知条件及第(1)小题与上相同,完全正确解答只能得到5分):
(2) 若点D的坐标为(1,0),求矩形DEFG的面积.
解:⑴ 解法一:设![]() ,
,
任取x,y的三组值代入,求出解析式![]() ,···································· 1分
,···································· 1分
令y=0,求出![]() ;令x=0,得y=-4,
;令x=0,得y=-4,
∴ A、B、C三点的坐标分别是A(2,0),B(-4,0),C(0,-4) . ···················· 3分
解法二:由抛物线P过点(1,-![]() ),(-3,
),(-3,![]() )可知,
)可知,
抛物线P的对称轴方程为x=-1,···································································· 1分
又∵ 抛物线P过(2,0)、(-2,-4),则由抛物线的对称性可知,
点A、B、C的坐标分别为 A(2,0),B(-4,0),C(0,-4) .····························· 3分
⑵ 由题意,![]() ,而AO=2,OC=4,AD=2-m,故DG=4-2m,············ 4分
,而AO=2,OC=4,AD=2-m,故DG=4-2m,············ 4分
又 ![]() ,EF=DG,得BE=4-2m,∴ DE=3m,···································· 5分
,EF=DG,得BE=4-2m,∴ DE=3m,···································· 5分
∴SDEFG=DG·DE=(4-2m) 3m=12m-6m2 (0<m<2) . ········································· 6分
注:也可通过解Rt△BOC及Rt△AOC,或依据△BOC是等腰直角三角形建立关系求解.
⑶ ∵SDEFG=12m-6m2 (0<m<2),∴m=1时,矩形的面积最大,且最大面积是6 .
当矩形面积最大时,其顶点为D(1,0),G(1,-2),F(-2,-2),E(-2,0),··· 7分
设直线DF的解析式为y=kx+b,易知,k=![]() ,b=-
,b=-![]() ,∴
,∴![]() ,
,
又可求得抛物线P的解析式为:![]() , ······································· 8分
, ······································· 8分
令![]() =
=![]() ,可求出x=
,可求出x=![]() . 设射线DF与抛物线P相交于点N,则N的横坐标为
. 设射线DF与抛物线P相交于点N,则N的横坐标为![]() ,过N作x轴的垂线交x轴于H,有
,过N作x轴的垂线交x轴于H,有
![]() =
=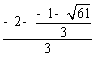 =
=![]() ,······················································ 9分
,······················································ 9分
点M不在抛物线P上,即点M不与N重合时,此时k的取值范围是
k≠![]() 且k>0. ····················································································· 10分
且k>0. ····················································································· 10分
说明:若以上两条件错漏一个,本步不得分.
若选择另一问题:
⑵ ∵![]() ,而AD=1,AO=2,OC=4,则DG=2,································· 4分
,而AD=1,AO=2,OC=4,则DG=2,································· 4分
又∵![]() , 而AB=6,CP=2,OC=4,则FG=3,
, 而AB=6,CP=2,OC=4,则FG=3,
∴SDEFG=DG·FG=6.
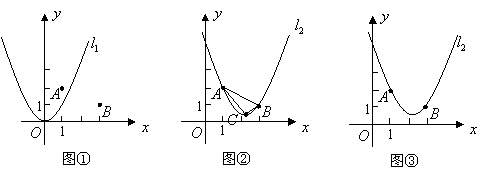
10、(2007山东威海)如图①,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,二次函数
,二次函数![]() 的图象记为抛物线
的图象记为抛物线![]() .
.
(1)平移抛物线![]() ,使平移后的抛物线过点
,使平移后的抛物线过点![]() ,但不过点
,但不过点![]() ,写出平移后的一个抛物线的函数表达式:
(任写一个即可).
,写出平移后的一个抛物线的函数表达式:
(任写一个即可).
(2)平移抛物线![]() ,使平移后的抛物线过
,使平移后的抛物线过![]() 两点,记为抛物线
两点,记为抛物线![]() ,如图②,求抛物线
,如图②,求抛物线![]() 的函数表达式.
的函数表达式.
(3)设抛物线![]() 的顶点为
的顶点为![]() ,
,![]() 为
为![]() 轴上一点.若
轴上一点.若![]() ,求点
,求点![]() 的坐标.
的坐标.
(4)请在图③上用尺规作图的方式探究抛物线![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 为等腰三角形.若存在,请判断点
为等腰三角形.若存在,请判断点![]() 共有几个可能的位置(保留作图痕迹);若不存在,请说明师.
共有几个可能的位置(保留作图痕迹);若不存在,请说明师.
 |
解:(1)有多种答案,符合条件即可.例如![]() ,
,![]() ,
,![]() 或
或![]() ,
,![]() ,
,![]() .
.
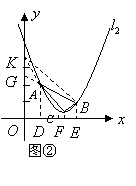 (2)设抛物线
(2)设抛物线![]() 的函数表达式为
的函数表达式为![]() ,
,
![]() 点
点![]() ,
,![]() 在抛物线
在抛物线![]() 上,
上,
![]() 解得
解得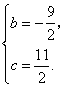
![]() 抛物线
抛物线![]() 的函数表达式为
的函数表达式为![]() .
.
(3)![]() ,
,![]() 点的坐标为
点的坐标为![]() .
.
过![]() 三点分别作
三点分别作![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() .
.
![]() .
.
延长![]() 交
交![]() 轴于点
轴于点![]() ,设直线
,设直线![]() 的函数表达式为
的函数表达式为![]() ,
,
![]() 点
点![]() ,
,![]() 在直线
在直线![]() 上,
上,![]() 解得
解得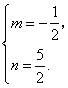
![]() 直线
直线![]() 的函数表达式为
的函数表达式为![]() .
.![]() 点的坐标为
点的坐标为![]() .
.
设![]() 点坐标为
点坐标为![]() ,分两种情况:
,分两种情况:
若![]() 点位于
点位于![]() 点的上方,则
点的上方,则![]() .连结
.连结![]() .
.
![]() .
.
![]() ,
,![]() ,解得
,解得![]() .
.![]() 点的坐标为
点的坐标为![]() .
.
若![]() 点位于
点位于![]() 点的下方,则
点的下方,则![]() .
. 同理可得,
同理可得,![]() .
.
![]() 点的坐标为
点的坐标为![]() .
.
(4)作图痕迹如图③所示.
由图③可知,点![]() 共有3个可能的位置.
共有3个可能的位置.
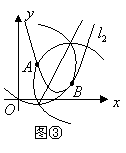
11、(2007浙江省)如图,抛物线![]() 与x轴交A、B两点(A点在B点左侧),直线
与x轴交A、B两点(A点在B点左侧),直线![]() 与抛物线交于A、C两点,其中C点的横坐标为2。
与抛物线交于A、C两点,其中C点的横坐标为2。
(1)求A、B 两点的坐标及直线AC的函数表达式;
(2)P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;
(3)点G抛物线上的动点,在x轴上是否存在点F,使A、C、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由。
解:(1)令y=0,解得![]() 或
或![]() (1分)
(1分)
∴A(-1,0)B(3,0);(1分)
将C点的横坐标x=2代入![]() 得y=-3,∴C(2,-3)(1分)
得y=-3,∴C(2,-3)(1分)
∴直线AC的函数解析式是y=-x-1
(2)设P点的横坐标为x(-1≤x≤2)(注:x的范围不写不扣分)
则P、E的坐标分别为:P(x,-x-1),(1分)
E(![]() (1分)
(1分)
∵P点在E点的上方,PE=![]() (2分)
(2分)
∴当![]() 时,PE的最大值=
时,PE的最大值=![]() (1分)
(1分)
(3)存在4个这样的点F,分别是![]()