二次函数单元测试（2）
（满分100分；完卷时间60分钟）
班级 姓名 成绩
一．选择题（每题3分，共24分）
1． 下列各式中，y是
的二次函数的是 (
)
A．
B．
C． 
D． 
2．已知点（2，8）在抛物线y=ax2上，则a的值为 （ ）
A、±2 B、±2
C、2
D、－2
3．二次函数y=x2＋4x＋a的最小值是2，则a的值是 （ ）
A、4 B、5 C、6 D、7
4．若二次函数
的图象经过原点，则
的值必为 ( )
A． 0或2 B． 0 C． 2 D． 无法确定
5．抛物线
则图象与轴交点为
（ ）
A． 二个交点 B． 一个交点 C． 无交点 D． 不能确定
6．对于
的图象下列叙述正确的是
（ ）
A 顶点坐标为(－3，2) B 对称轴为直线x=3
C 当x=3时，y有最大值2 D 当
时
随增大而减小
7．抛物线
向右平移1个单位，再向上平移2个单位得到
（ ）
A 
B 
C 
| |
|
的图象如图所示，则下列结论中正确的是： （ ）
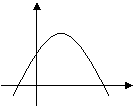
A a>0 b<0 c>0 B a<0 b<0 c>0
C a<0 b>0 c<0
| |
|
二．填空题：（每题3分，共30分）
9．抛物线y=－2x2－1的顶点坐标是 。
10．抛物线y=－2x2－x+3与y轴交点的坐标是 。
11．把二次函数y=－2x2＋4x+3化成y=a（x+h）2+k的形式是 。
12．已知函数y=x2+3kx+k+1的图象过（-1，4），那么
的值是 。
13．已知抛物线
的顶点在轴上，则的值是
。
14． 写出一个开口向上，且对称轴为直线
的二次函数解析式 。
15．若抛物线y=－x2+8x－12的顶点是P，与X轴的两个交点是C、D两点，则
PCD的面积是
。
16．已知二次函数
，则它的对称轴是直线
。
17．抛物线
与直线
的交点坐标是
。
18．已知二次函数
的最大值是3，则
的值是
。
三．解答题(共52分)
19．（6分）用配方法或公式法求二次函数
的对称轴、顶点坐标和最值。
20．（6分）已知一条抛物线过点
和
，且它的对称轴为直线
，试求这条抛物线的解析式。
21．（10分）已知二次函数的图象的顶点坐标为（3，-2）且与
轴交与（0，
）
（1）求这个二次函数的解析式，并画于它的图象；
（2）若这抛物线经过点
，试比较
的大小。
22．（12分）某水果批发商场经销一种高档水果，如果每千克盈利10元，每天可售出500千克，经市场调查发现，在进货价不变的情况下，若每千克涨价一元，日销售量将减少20千克。
（1）现要保证每天盈利6000元，同时又要让顾客得到实惠，那么每千克应涨价多少元？
（2）若该商场单纯从经济角度看，那么每千克应涨价多少元，能使商场获利最多。
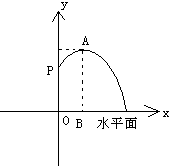
23．（12分）某市人民广场上要建造一个圆形的喷水池，并在水池中央垂直安装一个柱子OP，柱子顶端P处装上喷头，由P处向外喷出的水流（在各个方向上）沿形状相同的抛物线路径落下（如图所示）。若已知OP＝3米，喷出的水流的最高点A距水平面的高度是4米，离柱子OP的距离为1米。
（1）求这条抛物线的解析式；
（2）若不计其它因素，水池的半径至少要多少米，才能使喷出的水流不至于落在池外。
参考答案
一：选择题：1、C 2、C 3、C 4、A 5、B 6、B 7、A 8、D
二：填空题： 9、（0，-1） 10、（0，3） 11、
12、-1 13、2
14、例如
15、8 16、
17、（1，-1）（-2，8） 18、-1
三：解答题：
19．对称轴为直线，顶点坐标是
，当X=3时，Y有最大值。
20．
或
21．
，图象略！
。
22．解：1）、设每千克应涨价元，由题意得：
解得
，
要让顾客得到实惠则应每千克应涨价5元。
2）、设商场的利润为元，有：
当
时，的值最大，为6125元！
23．解：1）、设这条抛物线解析式为
由题意知：顶点A为（1，4），P为（0，3）
∴ 
，
，
。
所以这条抛物线的解析式为
。
2）、令
，则
，
所以若不计其它因素，水池的半径至少3米，才能使喷出的水流不至于落在池外。