06天河区初三数学辅导班资料6 四边形及平移旋转对称
一、 知识框图：
１、
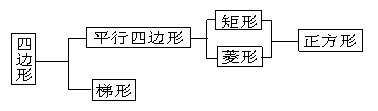
２、
３、
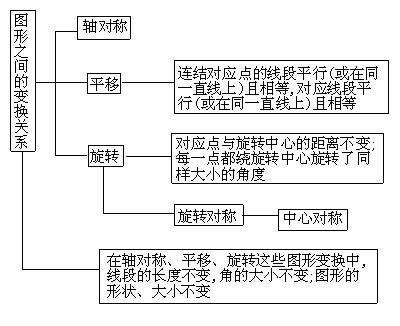
二、 例题分析
1、四边形
例1（1）凸五边形的内角和等于______度，外角和等于______度，
（2）若一凸多边形的内角和等于它的外角和， 则它的边数是_______.
2．平行四边形的运用
例2 如图,∠1=∠2,则下列结论一定成立的是( )
A. AB∥CD B. AD∥BC C. ∠B=∠D D. ∠3=∠4
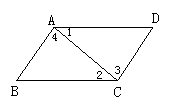若ABCD是平行四边形，则上述四个结论中那些是 正确？你还可以得到什么结论？
3．矩形的运用
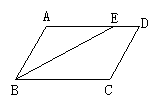
例3 如图1，EF过矩形ABCD对角线的交点O，且分别交AB、CD于E、则阴影部分的面积是矩形ABCD的面积的……………………………………………（ ）
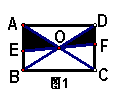A、
B、
C、
D、
4．菱形的运用
例4 1. 一个菱形的两条对角线的长的比是2 : 3 ,面积是12 cm2 , 则它的两条对角线的长分别为_____、____.
2、已知菱形的周长为40cm,两条对角线之比为3：4，则菱形的面积为_______.
5．等腰梯形的有关计算
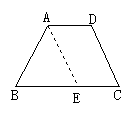例5 已知:如图,等腰梯形ABCD中,AD∥BC,AD=3,AB=4, BC=7.求∠B的度数..
6．轴对称的应用
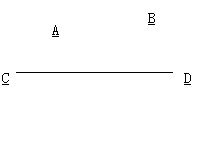
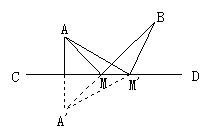
例6 如图,牧童在A处放牛,其家在B处,若牧童从A处出发牵牛到河岸CD边饮水后再回家,试问在何处饮水所走路程最短?
7．中心对称的运用
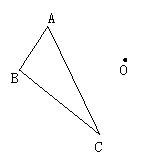
例7 如图,作△ABC关于点O的中心对称图形△DEF
8．平移作图
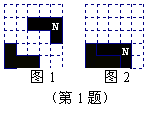例8 ．在5×5方格纸中将图（1）中的图形N平移后的位置如图（2）中所示，那么正确的平移方法是（ ）.
(A)先向下移动1格，再向左移动1格
(B)先向下移动1格，再向左移动2格
(C)先向下移动2格，再向左移动1格
(D)先向下移动2格，再向左移动2格
9．旋转的运用
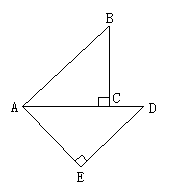例9 如图,△ABC和△ADE都是等腰直角三角形,∠C和∠AED都是直角,点C在AD上,如果△ABC经旋转后能与△ADE重合,那么哪一点是旋转中心?旋转了多少度?
解:_____是旋转中心,_______方向旋转了______.
基础达标
一、选择题：
1. 一个内角和是外角和的2倍的多边形是 边形.
2. 有以下四个命题:
(1)两条对角线互相平分的四边形是平行四边形.
(2)两条对角线相等的四边形是菱形.
(3)两条对角线互相垂直的四边形是正方形.
(4)两条对角线相等且互相垂直的四边形是正方形,其中正确的个数为( )
A.4 B.3 C.2 D.1
3．下面条件中，能判定四边形是平行四边形的条件是（ ）
A．一组对角相等 B．对角线互相平分
C．一组对边相等 D．对角线互相垂直
4．在一个平面上有不在同一直线上的三点，则以这三点为顶点的平行四边形有（ ）
A．1个 B．2个 C．3个 D．4个
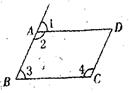
5. 如图,□ABCD中,∠C=108°,BE平分∠ABC,则∠ABE等于( )
A.18° B.36° C.72° D.108°
6、下列说法中，正确的是（ ）
B
A 、等腰梯形既是中心对称图形又是轴对称图形．
B 、正方形的对角线互相垂直平分且相等
C 、矩形是轴对称图形且有四条对称轴
D 、菱形的对角线相等
7、如图，在平行四边形ABCD中，下列各式不一定正确的是（ ）
A．
B．
C．
D．
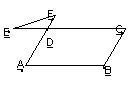8、在平行四边形ABCD中，
，延长AD至F，延长CD至E，连接EF，则
（ D ）
（A）
（B）
（C）
（D）
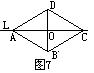9、如图7，直线
是四边形ABCD的对称轴，若AB=CD，有下面的结论：①AB∥CD；②AC⊥BD；③AO=OC；④AB⊥BC，其中正确的结论有____①②③_____。
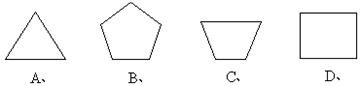
10.如图,观察下列图形,既是轴对称图形又是中心对称图形的个数是( ) .
A.3个 B.4个 C.5个 D.6个
 |
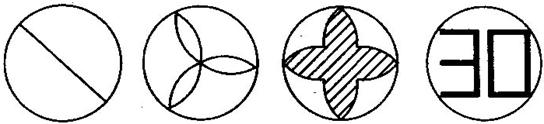
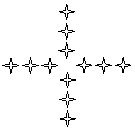11．下列基本图形中，经过平移、旋转或轴对称变换后，不能得到右图的是( )
A． B．
 | |||
 | |||
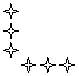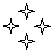C. Ｄ．
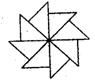12．右图可以看作是一个等腰直角三角形旋转若干次而生成的则
每次旋转的度数可以是（ ）
A．900 B．600
C．450 D．300
13．图2是我国古代数学赵爽所著的《勾股圆方图注》中
所画的图形，它是由四个相同的直角三角形拼成的，下面关于此图形的说法正确的是( )
A．它是轴对称图形，但不是中心对称图形
B．它是中心对称图形，但不是轴对称图形
C．它既是轴对称图形，又是中心对称图形
D．它既不是轴对称图形，又不是中心对称图形
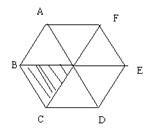
14、下图可以看作是一个等腰直角三角形旋转若干次而生成的则每次旋转的度数可以是（ ）
A．900 B．600 C．450 D．300
|
14 图15
15、如上图，O是正六边形ABCDE的中心，下列图形中可由△OBC平移得到的是 （ ）
C A．△OCD B．△OAB C．△OAF D．OEF
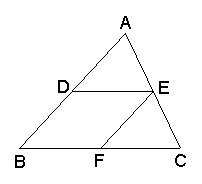
16.如图,D、E、F是△ABC三边的中点,且DE∥AB,DF∥AC,EF ∥BC, 平移△AEF可以得到的三角形是( )
A.△BDF B.△DEF C.△CDE D.△BDF和△CDE
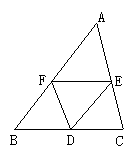
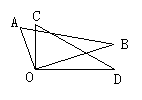
图16 图17
17.将两块直角三角尺的直角顶点重合为如图17的位置, 若∠AOD=110°,则∠BOC=____°
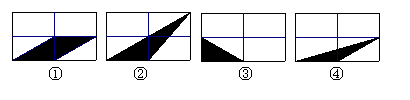18、如图将四个全等的矩形分别等分成四个全等的小矩形，其中阴影部分面积相等的是( )
A．只有①和②相等 B．只有③和④相等
C．只有①和④相等 D．①和②，③和④分别相等
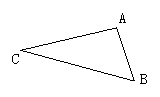
19.如图,已知△ABC,画出△ABC绕点C逆时针旋转90°后的图形.
20、矩形纸片ABCD中，AD=4cm ，AB=10cm，按如图方式折叠，使点B与点D重合，折痕为EF，则DE=
cm.
21、若四边形的两条对角线相等，则顺次连结该四边形各边中点所得的四边形是( )
A.梯形 B.矩形 C.菱形 D.正方形
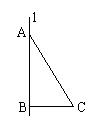
22． 如图：已知在Rt△ABC中，∠ABC=90°，∠C＝60°，边AB=6cm.
（1） 求边AC和BC的值；
（2） 求以直角边AB所在的直线l为轴旋转一周所得的几何体的侧面积.
(结果用含π的代数式表示)
解：
证明：∵DE∥BC,EF∥AB,
∴四边形BDEF是平行四边形 ∴DE=BF
∵F是BC的中点 ∴BF=CF ∴DE=CF
23、（2005常州市）如图，在
中，点
、
、
分别在
、
、
上，
，
，且是的中点．
求证：
证： ⑴∵AD∥BC ∴AD∥CE 又∵DE∥AC ∴四边形ACED是平行四边形 ⑵过D点作DF⊥BE于F点 ∵DE∥AC，AC⊥BD ∴DE⊥BD，即∠BDE=90°
由⑴知DE=AC，CE=AD=3 ∵四边形ABCD是等腰梯形 ∴AC=DB
∴DE=DB ∴△DBE是等腰直角三角形，∴△DFB也是等腰直角三角形
∴DF=BF=
(7－3)+3=5 (也可运用：直角三角形斜边上的中线等于斜边的一半“)
注：⑴过对角线交点O作OF⊥BC于F，延长FO交AD于H，于是OH⊥AD由△ABC≌△DCB，得到△OBC是等腰直角三角形，OF=BC=
同理OH=AD=
，高HF=
⑵过A作AF⊥BC于F，过D作DH⊥BC于H，由△AFC≌△DHB 得高AF=FC=
(AD+BC)=5⑶
(进行计算)
解：（1）当CE＝4时，四边形ABED是等腰梯形。 理由如下：
在BC上截取CE＝AD，连结DE、AE，∵AD∥BC， ∴四边形AECD是平行四边形。
∴AE＝CD＝BD。 ∵BE＝12－4＝8＞4，即BE＞AD， ∴AB不平行于DE，
∴四边形ABED是梯形。 ∵AE∥CD，CD＝BD， ∴∠AEB＝∠C＝∠DBC。
在△ABE和△DEB中，
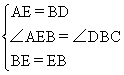∴△ABE≌△DEB （SAS）。
∴AB＝DE，
∴四边形ABED是等腰梯形。 （也可不作辅助线，通过证明△ABD≌EDC而得AB＝DE）
（2）当C
＝6时，四边形ABD是直角梯形。 理由如下： 在BC上取一点，使C＝B＝
＝6，连结D， ∵BD＝CD ∴D⊥BC 又∵B≠AD，AD∥B， ∴AB不平行于D ∴四边形ABD是直角梯形。
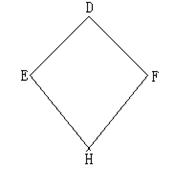
24．三月三，放风筝，小明制了一个风筝，如右图，且DE=DF，EH=FH，小明不用度量就知道∠DEH = ∠DFH。请你用所学过的数学知识证明之。（提示：可连结DH，证明 ΔDHE≌ΔDHF或连结EF，通过证明等腰三角形得证。）
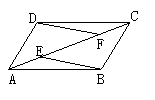
25.如图,E、F是□ABCD的对角线AC上两点,AE=CF.
求证:(1)△ABE≌△CDF.(2)BE∥DF.
（B层）
25、如图，在□ 
中，
是对角线
的中点，过点作的垂线与边、
分别交于、，求证：四边形
是菱形.
26.(2004.上海)如图1,边长为3的正方形ABCD绕点C按顺时针方向旋转30 °后得到正方形EFCG,EF交AD于点H,那么DH的长为________.
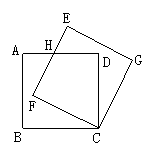
27．如图，已知正方形ABCD的边长为2.如果将线段BD 绕着点B旋转后，点D落在CB的延长线上的D′点处，
那么
′等于__________
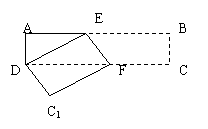
29、（2005广东省）如图，等腰梯形ABCD中，AD∥BC，M、N分别是AD、BC的中点，E、F分别是BM、CM的中点。
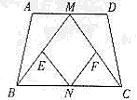（1）求证：四边形MENF是菱形；
（2）若四边形MENF是正方形，请探索等腰梯形ABCD的高和底边BC的数量关系，并证明你的结论。
四边形及平移旋转对称答案
二、考题例析
例1 (n - 2)·1800 =3600.解得 n=4. 例2 答案:B. 例3（ B ）
例4_____4cm,6cm ___
_____.
例5答案:∠B=60°.
例6．中心对称的运用
例7
例8 ．(C)
例9 点A是旋转中心,顺时针方向旋转了45.
基础达标
一、选择题：
1. 6 2. D.3．（ B ） 4．（ C）5 ( B )6、（B 7、（D8、（D）9、（①AB∥CD；②AC⊥BD；③AO=OC； 10.( B ).11．C. 12．（ C ）13．B．14（C）15、 D． 16. (D ) 17.(_70°18、 ( D)
19.
20、DE= 5。8 cm.21、 C.菱形
22．解：（1）AC＝
cm，BC＝
cm
（2）所求几何体的侧面积S＝
（
）
23、∵，
∴四边形DBFE是平行四边形
∴ DE=BF,
∵ 是的中点．
∴BF=CF
∴
证明：∵DE∥BC,EF∥AB,
∴四边形BDEF是平行四边形 ∴DE=BF
∵F是BC的中点 ∴BF=CF ∴DE=CF
24．：可连结DH，证明 ΔDHE≌ΔDHF或连结EF，通过证明等腰三角形得证。
证： ⑴∵AD∥BC ∴AD∥CE 又∵DE∥AC ∴四边形ACED是平行四边形
⑵过D点作DF⊥BE于F点 ∵DE∥AC，AC⊥BD ∴DE⊥BD，即∠BDE=90°
由⑴知DE=AC，CE=AD=3 ∵四边形ABCD是等腰梯形 ∴AC=DB
∴DE=DB ∴△DBE是等腰直角三角形，∴△DFB也是等腰直角三角形
∴DF=BF=(7－3)+3=5 (也可运用：直角三角形斜边上的中线等于斜边的一半“)
注：⑴过对角线交点O作OF⊥BC于F，延长FO交AD于H，于是OH⊥AD由△ABC≌△DCB，得到△OBC是等腰直角三角形，OF=BC=
同理OH=AD=，高HF=⑵过A作AF⊥BC于F，过D作DH⊥BC于H，由△AFC≌△DHB 得高AF=FC=(AD+BC)=5⑶(进行计算)
解：（1）当CE＝4时，四边形ABED是等腰梯形。 理由如下：
在BC上截取CE＝AD，连结DE、AE，∵AD∥BC， ∴四边形AECD是平行四边形。
∴AE＝CD＝BD。 ∵BE＝12－4＝8＞4，即BE＞AD， ∴AB不平行于DE，
∴四边形ABED是梯形。 ∵AE∥CD，CD＝BD， ∴∠AEB＝∠C＝∠DBC。
在△ABE和△DEB中，
∴△ABE≌△DEB （SAS）。
∴AB＝DE，
∴四边形ABED是等腰梯形。 （也可不作辅助线，通过证明△ABD≌EDC而得AB＝DE）
（2）当C＝6时，四边形ABD是直角梯形。 理由如下： 在BC上取一点，使C＝B＝＝6，连结D， ∵BD＝CD ∴D⊥BC 又∵B≠AD，AD∥B， ∴AB不平行于D ∴四边形ABD是直角梯形。
25.(1)证明:∵在△ABC与△EFD中,AB=EF,由EF∥AB得∠BAC=∠FED.由AD= CE得AC=ED.
∴△ABC≌△EFD.
(2)四边形BDFC是平行四边形.
证明:∵△ABC≌△EFD,
∴BC=FD,∠BCA=∠EDF.
∴BC∥FD
∴四边形BDFC是平行四边形.
26剖析：解题时，注意区分判定定理与性质定理的不同使用.
∵□ 中，
∥
，∴
.
又
，
.
∴△
≌△
，∴
.
∴四边形是平行四边形
.
又
，∴□ 是菱形.
27. _
_______.
28___
_______
29、
