中考数学四边形提高测试

《四边形》提高测试

（一）选择题（每小题4分，共32分）

1．若一个多边形的内角和是外角和的5倍，则这个多边形的边数是…………………（　　）

（A）9　　　　 （B）10　　　　（C）11　　　　 （D）12

【提示】为了便于计算，设每个内角都相等，那么每个内角是每个外角的5倍．

【答案】D．

2．已知菱形ABCD的两条对角线之和为l，面积为S，则它的边长为…………………（　　）

（A）　 （B）　（C）　 （D）

【提示】设两对角线长的一半为a与b，则S＝2 ab，l＝2（a＋b），边长为．利用a²＋b²＝(a＋b)²－2 ab．

【答案】C．

3．如图，矩形ABCD的边长AB＝6，BC＝8，将矩形沿EF折叠，使C点与A点重合，

则折痕EF的长是……………………………………………………………………（　　）

（A）7．5　 　　　 （B）6　　　　　 （C）10　　　　　 （D）5

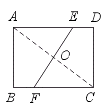
【提示】设AE＝x，则ED＝8－x，CE＝x，用勾股定理列出方程x²＝(8－x)²＋6²，解出x＝，而OA＝AC＝5．

【答案】A．

4．已知：如图，在□ABCD中，E、F分别是边AD、BC的中点，AC分别交BE、DF

于G、H，并有下列结论：

（1）BE＝DF；　　　　　 （2）AG＝GH＝HC；

（3）EG＝BG；　　　　 （4）S_△ABE＝3 S_△AGE．

其中正确的结论有…………………………………………………………………（　　）

（A）1个　　　　（B）2个　　 （C）3个　　　　（D）4个

【提示】BG＝2 FH＝2 GE．

【答案】D．

5．如图，E为矩形ABCD的边CD上的一点，AB＝AE＝4，BC＝2，则∠BEC是（　　）

（A）15°　　（B）30°　　（C）60°　　（D）75°

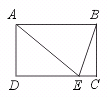
【提示】作EF⊥AB于F点，则由AE＝2 BC＝2 EF，得知∠EAB＝30°．

【答案】D．

6．顺次连结四边形各边中点所得四边形是矩形，则原图形一定是………………（　　）

（A）菱形　　　　　　　　  （B）对角线相等的四边形

（C）对角线垂直的四边形　　（D）对角线垂直且互相平分的四边形

【答案】C．

7．如图，周长为68的矩形ABCD被分成7个全等的矩形，则矩形ABCD的面积为………………………………………………………………………………………（　　）

（A）98　 　　 （B）196　 　　 （C）280　　 　 （D）284

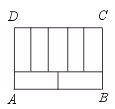
【提示】设小矩形的长为x，宽为y，则有

∴　x＝10，y＝4． xy＝40．

【答案】C．

8．如图，在□ABCD中，EF∥BC，GH∥AB，EF、GH的交点P在BD上，则图中面积相等的平行四边形有…………………………………………………………（　　）

（A）0对　　　 （B）1对　　　 （C）2对　　　（D）3对

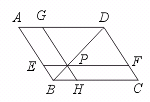
【提示】由S_△BPE＝S_△BPH，S_△PDG＝S_△PDF和S_△ABD＝S_△CBD可知有一边过P点的3对平行四边形面积相等．

【答案】D．

（二）填空题（每小题3分，共18分）

9．一个多边形的一个内角的补角与其他内角的和恰为500°，那么这个多边形的边数是______．

【提示】由于五边形内角和为540°＞500°，所以多边形的边数不可能超过5．显然它不可能是三角形．因此分四边形、五边形两种情况验证是否存在符合要求的图形．

【答案】4或5．

10．如图，P是□ABCD内的一点，＝，则＝______．

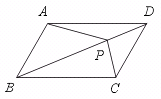
【提示】过P点分别作AB和BC的平行线，与□ABCD的边相交，找出4对全等三角形．由此可见，△ABP与△CDP的面积之和为□ABCD面积的一半．

【答案】．

11．用任意两个全等的直角三角形拼下列图形：

①平行四边形　 ②矩形　　　　  ③菱形

④正方形　　　 ⑤等腰三角形　　⑥等边三角形

其中一定能够拼成的图形是_______（只填题号）．

【答案】①②⑤．

12．如图，如果四边形CDEF旋转后能与正方形ABCD重合，那么在图形所在平面内，可以作为旋转中心的点的个数为______．

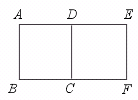
【提示】施转中心必须在公共边CD上．

【答案】3．

13．如图，梯形ABCD中，△ABP的面积为20平方厘米，△CDQ的面积为35平方厘米，则阴影四边形的面积等于______平方厘米．

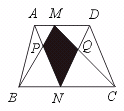
【提示】连结MN．S_△MNP＝S_△ABP，S_△MNQ＝S_△CDQ．

【答案】55．

14．如图，将边长为1的正方形ABCD绕A点按逆时针方向旋转30°，至正方形

AB′C′D′，则旋转前后正方形重叠部分的面积是________．

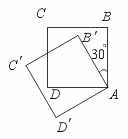
【提示】设CD与B′C′的交点为M，则AM为两正方形的对称轴．又设MD＝x，则AM＝2 x，用勾股定理列方程并解之即可．

【答案】．

（三）计算题（每小题6分，共12分）

15．如图，一个等腰梯形的两条对角线互相垂直，且中位线长为l，求这个等腰梯形的高．

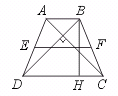
【提示】如下图，过B点作AC的平行线．

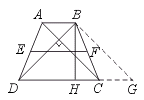
【答案】过B作BG∥AC，交DC的延长线于G点．

在梯形ABCD中，AB∥DC，

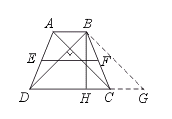∴　四边形ABGC为平行四边形．

∴　CG＝AB，BG＝AC．

∵　EF为梯形中位线，

∴　DG＝DC＋AB＝2 EF＝2 l．

∵　AC⊥BD且AC＝BD．

∴　BG⊥BD且BG＝BD．

∴　△BDG为等腰直角三角形．

∴　高BH＝DG＝l．

16．如图，矩形纸片ABCD中，AB＝3 cm，BC＝4 cm．现将A，C重合，使纸片

折叠压平，设折痕为EF，试求AF的长和重叠部分△AEF的面积．

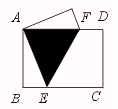
【提示】把AF取作△AEF的底，AF边上的高等于AB＝3．

由折叠过程知，EF经过矩形的对称中心，FD＝BE，AE＝CE＝AF．由此可以在

△ABE中使用勾股定理求AE，即求得AF的长．

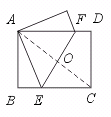
【答案】如图，连结AC，交EF于点O，

由折叠过程可知，OA＝OC，

∴　O点为矩形的对称中心．E、F关于O点对称，B、D也关于O点对称．

∴　BE＝FD，EC＝AF，

由EC折叠后与EA重合，

∴　EC＝EA．

设AF＝x，则BE＝FD＝AD－AF＝4－x，AE＝AF＝x．

在Rt△ABE中，由勾股定理，得

AB²＋BE²＝AE²，即　3²＋(4－x) ²＝x²．

解得　x＝．

∴　S_△AEF＝×3×＝（cm²）

故AF的长为cm，△AEF的面积为cm²．

（四）证明题（每小题5分，共20分）

17．已知：如图，梯形ABCD中，AD∥BC，过C作CE∥AB且CE＝AB，连结

DE交BC于F．求证：DF＝EF．

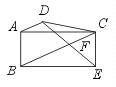
【提示】连结AE交BC于O，要证DF＝EF，因为AD∥BC，所以只要证OA＝OE，只要证四边形ABEC为平行四边形．

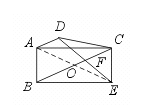【答案】连结AE交BC于O点，

∵　CEAB，

∴　四边形ABEC为平行四边形，

∴　OA＝OE．

又　AD∥BC，

∴　DF＝EF．

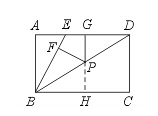
18．如图，E是矩形ABCD的边AD上一点，且BE＝ED，P是对角线BD上任意一点，PF⊥BE，PG⊥AD，垂足分别为F、G．求证：PF＋PG＝AB．

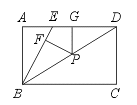
【提示】延长GP交BC于H，只要证PH＝PF即可，所以只要证∠PBF＝∠PBH．

【答案】∵　BE＝DE，

∴　∠EBD＝∠EDB．

∵　在矩形ABCD中，AD∥BC，

∴　∠DBC＝∠ADB，

∴　∠EBD＝∠CBD．

延长GP交BC于H点．

∵　PG⊥AD，

∴　PH⊥BC．

∵　PF⊥BE，P是∠EBC的平分线上．

∴　PF＝PH．

∵　四边形ABHG中，

∠A＝∠ABH＝∠BHG＝∠HGA＝90°．

∴　四边形ABHG为矩形，

∴　AB＝GH＝GP＋PH＝GP＋PF

故　PF＋PG＝AB．

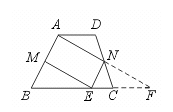
19．如图，在梯形ABCD中，AD∥BC，M、N分别是AB、CD的中点，ME∥AN交BC于点E，求证AM＝NE．

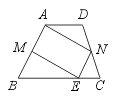
【提示】延长AN交BC延长线于点F．证明NE为△ABF的中位线．

【答案】延长AN交BC的延长线于点F，

∵　DN＝CN，∠AND＝FNC，

又由AD∥BC，得∠ADN＝∠FCN，

∴　△ADN≌△FCN．

∴　AN＝NF．

∵　AM＝BM且ME∥AF，

∴　BE＝EF．

∴　NE为△ABF的中位线，

∴　NE＝AB＝AM．

20．已知：如图，以正方形ABCD的对角线为边作菱形AEFC，B在FE的延长线上．

求证：AE、AF把∠BAC三等分．

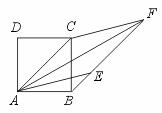
【提示】证出∠CAE＝30°即可．

【答案】连结BD，交AC于点O，作EG⊥AC，垂足为G点．

∵　四边形AEFC为菱形，

∴　EF∥AC．

∴　GE＝OB．

∵　四边形ABCD为正方形，

∴　OB⊥AC，

∴　OBGE，

∵　AE＝AC，OB＝BD＝AC，

∴　EG＝AE，

∴　∠EAG＝30°．

∴　∠BAE＝15°．

在菱形AEFC中，AF平分∠EAC，

∴　∠EAF＝∠FAC＝∠EAC＝15°

∴　∠EAB＝∠FAE＝∠FAC．

即AE、AF将∠BAC三等分．

（五）解答题（每小题6分，共18分）

21．如图，已知M、N两点在正方形ABCD的对角线BD上移动，∠MCN为定角a，

连结AM、AN，并延长分别交BC、CD于E、F两点，则∠CME与∠CNF在M、

N两点移动过程，它们的和是否有变化？证明你的结论．

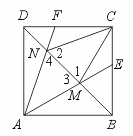
【提示】BD为正方形ABCD的对称轴，

∴　∠1＝∠3，∠2＝∠4，

用∠1和∠2表示∠MCN以及∠EMC＋∠FNC．

【答案】∵　BD为正方形ABCD的对称轴，

∴　∠1＝∠3，∠2＝∠4，

∴　∠EMC＝180°－∠1－∠3＝180°－2∠1．

同理　∠FNC＝180°－2∠2．

∴　∠EMC＋∠FNC＝360°－2（∠1＋∠2）．

∵　∠MCN＝180°－（∠1＋∠2），

∴　∠EMC＋∠FNC总与2∠MCN相等．

因此∠EMC＋∠FNC始终为定角，这定角为∠MCN的2倍．

22．如图（1），AB、CD是两条线段，M是AB的中点，S_△DMC、S_△DAC和S_△DBC分别

表示△DMC、△DAC、△DBC的面积．当AB∥CD时，有

S_△DMC＝　 　　　　①

（1）如图（2），若图（1）中AB∥CD时，①式是否成立？请说明理由．

（2）如图（3），若图（1）中AB与CD相交于点O时，S_△DMC与S_△DAC和S_△DBC有何种相等关系？证明你的结论．

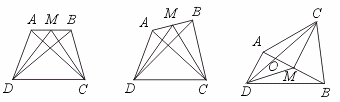
图（1）　　　　  图（2）　　　　　 图（3）

【提示】△DAC，△DMC 和△DBC 同底CD，通过它们在CD 边上的高的关系，来确定它们面积的关系．

【答案】（1）当AB∥CD时，①式仍成立．

分别过A、M、B作CD的垂线，AE、MN、BF的垂足分别为E、N、F．

∵　M为AB的中点，

∴　MN＝（AE＋BF）．

∴　S_△DAC＋S_△DBC＝DC·AE＋DC·BF＝DC·（AE＋BF）＝2 S_△DMC．

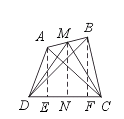∴　S_△DMC＝

（2）对于图（3）有S_△DMC＝．

证法一：∵　M是AB的中点，S_△ADM＝S_△BDM，S_△ACM＝S_△BCM，

S_△DBC＝S_△BDM＋S_△BCM＋S_△DMC，　　　　　　　　　  ①

S_△DAC＝S_△ADM＋S_△ACM－S_△DMC　　　　　　　　　　 ②

①－②得：S_△DBC－S_△DAC＝2 S_△DMC

∴　S_△DMC＝．

证法二：如右图，过A作CD的平行线l，MN⊥l，垂足为N，BE⊥l，垂足为E．设A、M、B到CD的距离分别h₁、h₀、h₂．则MN＝h₁＋h₀，BE＝h₂＋h₁．

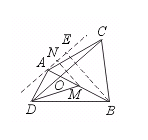
∵　AM＝BM，

∴　BE＝2 MN．

∴　h₂＋h₁＝2（h₁＋h₀），

∴　h₀＝．

∴　S_△DMC＝．

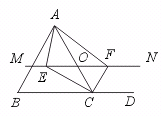
23．已知：如图，△ABC中，点O是AC上边上一个动点，过点O作直线MN∥BC，

MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F．

（1）求证EO＝FO．

（2）当点O运动到何处时，四边形AECF是矩形？证明你的结论．

【提示】（1）证明OE＝OC＝OF；

（2）O点的位置首先满足四边形AECF是平行四边形，然后证明它此时也是矩形．

【答案】（1）∵　CE平分∠BCA，

∴　∠BCE＝∠ECO．

又　MN∥BC，

∴　∠BCE＝∠CEO．

∴　∠ECO＝∠CEO．

∴　OE＝OC．

同理　OC＝OF．

∴　OE＝OF．

（2）当点O运动到AC边的中点时，四边形AECF是矩形，证明如下：

∵  OE＝OF，又O是AC的中点，

即　OA＝OC，

∴　四边形AECF是平行四边形．

∵　CE、CF分别平分∠BCA、∠ACD，且∠BCA＋∠ACD＝180°，

∴　∠ECF＝∠ECO＋∠OCF＝（∠BCA＋∠ACD）＝90°．

∴　□AECF是矩形．