中考复习系列《图形的认识》
第三课时 四边形
初三( )班 学号: 姓名:
一、多边形的有关概念
1、三角形形的内角和等于 。
2、四边形的内角和等于 。
3、n边形的内角和等于 。
4、n边形的外角和等于 。
二、几种特殊四边形的特征:
| 图形 | 边 | 角 | 对角线 | 对称性 |
| 平行 四边形 | 对边 且 | 对角 | 对角线 | 对称 |
| 矩形 | 对边 且 | 四个角都是
| 1、 2、 | |
| 菱形 | 对边 四边都 | 对角 | 对角线
每条对角线
| |
| 正方形 | 对边 四边都 | 四个角都是
| ||
| 等腰梯形 | 两底边 两腰 | 同一个底上的
|
二、几种特殊四边形的识别方法:
| 平行四边形 | ① 组对边分别 的四边形是平行四边形 ② 组对边分别 的四边形是平行四边形 ③有 组对边 的四边形是平行四边形 ④ 组对 分别 的四边形是平行四边形 ⑤对角线 的四边形是平行四边形 |
| 矩形 | ①有 的 四边形是矩形。 ②有 的四边形是矩形 ③对角线 且 的四边形是矩形 ④对角线 的 四边形是矩形 |
| 菱形 | ① 的四边形是菱形 ②有 组 的 四边形是菱形 ③对角线 的 四边形是菱形 ④对角线 的四边形是菱形 |
| 正方形 | ①有 的矩形是正方形 ②有 的菱形是正方形 ③对角线 的四边形是正方形 ④对角线 的矩形是正方形 ⑤对角线 的菱形是正方形 |
四、梯形
1、定义:一组对边 另一组对边 的四边形叫做梯形,平行的两边叫做梯形的 ,不平行的两边叫做梯形的 ,两底的距离叫做梯形的 。
2、一腰垂直于底的梯形叫做 梯形。
3、两腰相等的梯形叫做 梯形。
4、等腰梯形的性质
(1)等腰梯形同一底边上的两个内角 。
(2)等腰梯形的对角线 。
5、等腰梯形的识别
(1)同一底边上的两个内角 的梯形是等腰梯形。
(2)对角线 的梯形是等腰梯形。
6、三角形、梯形的中位线
连结梯形 的线段叫做梯形的中位线。
定理:梯形的中位线平行于 ,且等于 。
7、解决梯形问题,添加辅助线的常见方法:
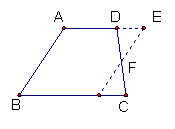
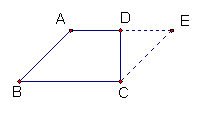
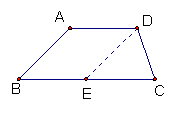
梯形内平移一腰 梯形外平移一腰 过一腰中点平移另一腰
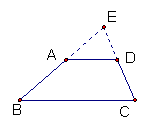
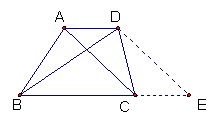
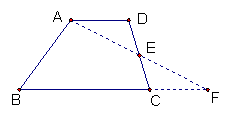 平移对角线
延长两腰
平移对角线
延长两腰
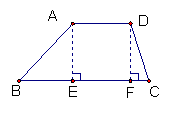
作高 连结一顶点与腰中点的线段并延长
五、面积、周长的计算方法
1、平行四边形的面积= ,周长= 。(边长为a,b,h为a边上的高)
2、菱形的面积= = ,周长= 。
(边长为a, h为a边上的高,两条对角线为c,d)
3、矩形的面积= ,周长= 。(边长为a,b)
4、正方形的面积= ,周长= 。(边长为a)
习题
1、下面条件中不能判别四边形是平行四边形的是( )
A.对角线互相平分 B.一组对边平行,另一组对边相等
C.一组对边平行且相等 D.一组对边平行,一组对角相等
2、下面不是平行四边形的特征的是( )
A.对角互补 B.邻角互补 C.对边平行 D.对角线互相平分
3、矩形有而菱形不一定有的特征是( )
A.邻边相等 B.对角线互相垂直平分
C.对角线相等且互相平分 D.有一组邻边相等
4、对角线相等的四边形一定是( )
A.矩形 B.菱形 C.正方形 D.以上答案都不对
5、正方形具有而矩形不具有的特征是( )
A.对边相等 B.对角线相等
C.对角线互相平分 D.对角线互相垂直
6.正方形具有而菱形不具有的特征是( )
A.对边相等 B.对角线相等
C.对角线互相平分 D.对角线互相垂直
7、在平行四边形ABCD的周长是20cm,且AB=6cm,则AC=
8、在平行四边形ABCD中,∠A=40度,∠C= ,∠B=
9、在平行四边形ABCD中,∠A-∠B=30度,则∠A= ,∠B=
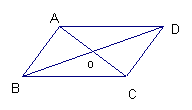 10、在平行四边形ABCD中,AC=12,
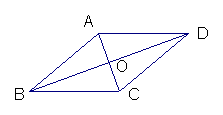
10、在平行四边形ABCD中,AC=12,
BD=18,CD=9,则△ABO的周长是
 |
11、如图,菱形ABCD中,AC与BD交于点O,
若∠DAB=140º,则∠ABO=
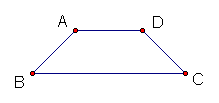 |
12、右图,在等腰梯形ABCD中,AD∥BC、
∠B=70º,则∠A= ,∠C= ,
∠D= 。
13、如果正多边形的一个外角为36°,那么这个多边形的边数有 条。
14、如果一个多边形的内角和为外角和的3倍,则这个多边形为 边形。
 15、菱形的两对角线长分别是10cm,4cm,则菱形的面积是
15、菱形的两对角线长分别是10cm,4cm,则菱形的面积是 ![]()
16、如图,菱形ABCD中,AC与BD交于点O,
若∠DAB=140º,则∠BAO=
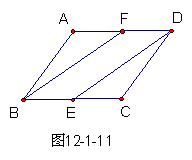 17、已知,如图12-1-11,在▱ABCD中,E是BC的中点,F是AD的中点,试说明四边形EBFD是平行四边形。
17、已知,如图12-1-11,在▱ABCD中,E是BC的中点,F是AD的中点,试说明四边形EBFD是平行四边形。
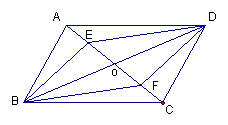 18、如图,已知▱ABCD,E、F分别是OA,OC的中点,求证:四边形BEDF是平行四边形。
18、如图,已知▱ABCD,E、F分别是OA,OC的中点,求证:四边形BEDF是平行四边形。
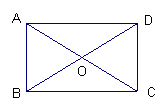
19、如图,矩形ABCD中,AC=8cm,△ABO的周长是11cm,求AB的长
 |
20、在梯形ABCD中,DC∥AB,∠A=50º,∠C=100º,若AB=12,DC=5,求BC的长
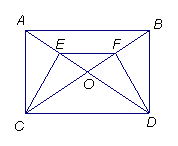
21、如图,矩形ABCD的对角线AC,BD相交于点O,E,F分别是OA,OB的中点,
(1) 求证:![]() ADE≌
ADE≌![]() BCF
BCF
(2) 若AD=4cm,AB=8cm,求CF的长。
22、如图,平行四边形ABCD中,AC与BD交于点O,
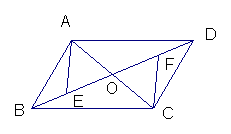 BE=DF,试说明(1)OE=OF
(2)AE=CF
BE=DF,试说明(1)OE=OF
(2)AE=CF
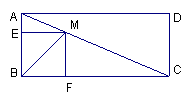
23、如图:矩形ABCD中,ME⊥AB于E,MF⊥BC于F,试说明四边形EBFM是矩形。
 |
24、如图:矩形BFEM中,∠B的平分线交对角线于M,试说明四边形EBFM是正方形。
 |
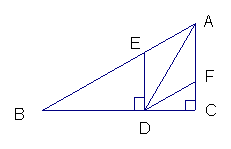 25、已知在△ABC中,∠C=90
25、已知在△ABC中,∠C=90![]() ,AD平分∠BAC,ED⊥BC交AB于E,DF∥AB交AC于F,说明四边形AFDE是菱形。
,AD平分∠BAC,ED⊥BC交AB于E,DF∥AB交AC于F,说明四边形AFDE是菱形。