中考数学四边形试题分类汇编
一、选择题
1、(2007福建福州)下列命题中,错误的是( )B
A.矩形的对角线互相平分且相等
B.对角线互相垂直的四边形是菱形
C.等腰梯形的两条对角线相等
 D.等腰三角形底边上的中点到两腰的距离相等
D.等腰三角形底边上的中点到两腰的距离相等
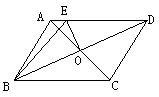
2、(2007山东日照)如图,在周长为20cm的□ABCD中,AB≠AD,AC、BD相交于点O,OE⊥BD交AD于E,则△ABE的周长为( )D
(A)4cm (B)6cm
(C)8cm (D)10cm
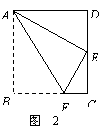 3、(2007山东东营)如图2,四边形ABCD为矩形纸片.把纸片ABCD折叠,使点B恰好落在CD边的中点E处,折痕为AF.若CD=6,则AF等于 ( )A
3、(2007山东东营)如图2,四边形ABCD为矩形纸片.把纸片ABCD折叠,使点B恰好落在CD边的中点E处,折痕为AF.若CD=6,则AF等于 ( )A
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)8
(D)8
4、(2007浙江义鸟)在下列命题中,正确的是( )C
A.一组对边平行的四边形是平行四边形 B.有一个角是直角的四边形是矩形
C.有一组邻边相等的平行四边形是菱形 D.对角线互相垂直平分的四边形是正方形
5、(2007甘肃陇南)顺次连结任意四边形各边中点所得到的四边形一定是 ( )A
A.平行四边形 B.菱形 C.矩形 D.正方形
6、(2007浙江绍兴)如图,在菱形ABCD中,对角线AC、BD相交于点O,E为BC的
 中点,则下列式子中一定成立的是( )B
中点,则下列式子中一定成立的是( )B
A.AC=2OE B.BC=2OE
C.AD=OE D.OB=OE
7、(2007四川眉山)下列命题中的假命题是( ).D
A.一组邻边相等的平行四边形是菱形
B.一组邻边相等的矩形是正方形
 c 一组对边平行且相等的四边形是平行四边形
c 一组对边平行且相等的四边形是平行四边形
D.一组对边相等且有一个角是直角的四边形是矩形
8、(2007天津市)在梯形ABCD中,AD//BC,对角线AC⊥BD,且![]() ,BD=12c m,则梯形中位线的长等于( )C
,BD=12c m,则梯形中位线的长等于( )C
A. 7.5cm B. 7cm C. 6.5cm D. 6cm
9、(2007浙江嘉兴)如图,在菱形ABCD中,不一定成立的( )C
(A)四边形ABCD是平行四边形 (B)AC⊥BD
(C)△ABD是等边三角形 (D)∠CAB=∠CAD
 10、(2007浙江金华)国家级历史文化名城——金华,风光秀丽,花木葱茏.某广场上一个形状是平行四边形的花坛(如图),分别种有红、黄、蓝、绿、橙、紫6种颜色的花.如果有
10、(2007浙江金华)国家级历史文化名城——金华,风光秀丽,花木葱茏.某广场上一个形状是平行四边形的花坛(如图),分别种有红、黄、蓝、绿、橙、紫6种颜色的花.如果有![]() ,
,![]() ,那么下列说法中错误的是( )C
,那么下列说法中错误的是( )C
A.红花、绿花种植面积一定相等
B.紫花、橙花种植面积一定相等
C.红花、蓝花种植面积一定相等
D.蓝花、黄花种植面积一定相等
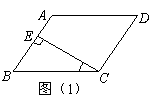 11、(2007四川乐山)如图(1),在平面四边形
11、(2007四川乐山)如图(1),在平面四边形![]() 中,
中,![]() ,
,![]() 为垂足.如果
为垂足.如果![]() ,则
,则![]() ( )B
( )B
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12、(2007四川成都)下列命题中,真命题是( )D
A.两条对角线相等的四边形是矩形
B.两条对角线互相垂直的四边形是菱形
C.两条对角线互相垂直且相等的四边形是正方形
D.两条对角线互相平分的四边形是平行四边形
二、填空题
 1、(2007浙江嘉兴)四边形的内角和等于__________.360°
1、(2007浙江嘉兴)四边形的内角和等于__________.360°
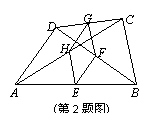
2、(2007山东临沂)如图,在四边形ABCD中,E、F、G、H分别是AB、BD、CD、AC的中点,要使四边形EFGH是菱形,四边形ABCD还应满足的一个条件是 。
答案:AD=BC,或ABCD为等腰梯形(答案不唯一)
 3、(2007天津)已知矩形ABCD,分别为AD和CD为一边向矩形外作正三角形ADE和正三角形CDF,连接BE和BF,则
3、(2007天津)已知矩形ABCD,分别为AD和CD为一边向矩形外作正三角形ADE和正三角形CDF,连接BE和BF,则![]() 的值等于 。1
的值等于 。1
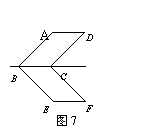
4、(2007河北省)如图7,若□ABCD与□EBCF关于BC所在直线对称,∠ABE=90°,则∠F = °.45
 5、(2007甘肃陇南)顺次连结任意四边形各边中点所得到的四边形一定是__ ___.平行四边形
5、(2007甘肃陇南)顺次连结任意四边形各边中点所得到的四边形一定是__ ___.平行四边形
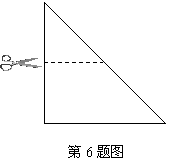
6、(2007湖南怀化)如图,将一张等腰直角三角形纸片沿中位线剪开可以拼成不同形状的四边形,请写出其中一种四边形的名称 .
答案:平行四边形、矩形、等腰梯形(三种中任选一种均给满分)
7、菱形的两条对角线长分别是6和8,则菱形的边长为 。5
 8、(2007甘肃陇南)如图,矩形
8、(2007甘肃陇南)如图,矩形![]() 的对角线
的对角线![]() 和
和![]() 相交于点
相交于点![]() ,过点
,过点![]() 的直线分别交
的直线分别交![]() 和
和![]() 于点E、F,
于点E、F,![]() ,则图中阴影部分的面积为 .3
,则图中阴影部分的面积为 .3
9、(2007四川成都)如图,把一张矩形纸片![]() 沿
沿![]() 折叠后,点
折叠后,点![]() 分别落在
分别落在![]() 的位置上,
的位置上,![]() 交
交![]() 于点
于点![]() .已知
.已知![]() ,那么
,那么![]()
![]() .64
.64
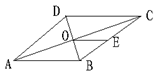
10、(2007四川成都)如图,如果要使![]() 成为一个菱形,需要添加一个条件,那么你添加的条件是
成为一个菱形,需要添加一个条件,那么你添加的条件是
 .
.
![]() 等;
等;
三、解答题
1、(2007浙江杭州市)我们学习了四边形和一些特殊的四边形,右图表示了在某种条件下它们之间的关系。
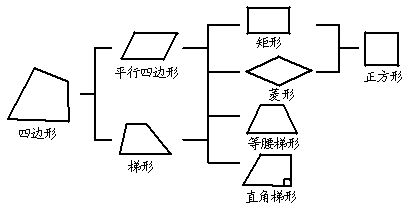 如果①,②两个条件分别是:①两组对边分别平行;②有且只有一组对边平行。那么请你对标上的其他6个数字序号写出相对应的条件。
如果①,②两个条件分别是:①两组对边分别平行;②有且只有一组对边平行。那么请你对标上的其他6个数字序号写出相对应的条件。
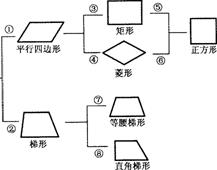
解:③有一个内角为直角;④一组邻边相等;⑤一组邻边相等;⑥有一个内角为直角;
⑦两腰相等;⑧一条腰垂直于底边。
2、(2007浙江临安)已知:如图,E、F是平行四边行ABCD的对角线AC上的两点,AE=CF。
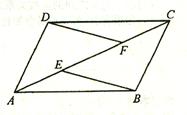 求证:(1)△ADF≌△CBE;(2)EB∥DF。
求证:(1)△ADF≌△CBE;(2)EB∥DF。
证明:(1)∵AE=CF
∴AE+EF=CF+FE即AF=CE --------- 1分
又ABCD是平行四边形,∴AD=CB,AD∥BC
∴∠DAF=∠BCE ---------2分
在△ADF与△CBE中
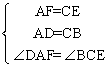 ---------3分
---------3分
∴△ADF≌△CBE(SAS)---------4分
(2)∵△ADF≌△CBE
∴∠DFA=∠BEC ---------5分
∴DF∥EB---------6分
3、(2007恩施自治州)如图7,平行四边形ABCD的对角线AC、BD相交于点O,E、F是直线AC上的两点,并且AE=CF,求证:四边形BFDE是平行四边形.
证明:∵四边形ABCD是平行四边形
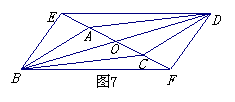 ∴OA=OC,OB=OD
(4分)
∴OA=OC,OB=OD
(4分)
又∵AE=CF
∴OE=OF (6分)
∴四边形BFDE是平行四边形 (8分)
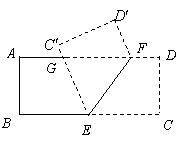
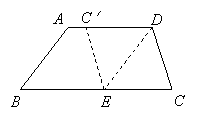 4、(2007云南双柏)如图,在梯形纸片ABCD中,AD//BC,AD>CD,将纸片沿过点D的直线折叠,使点C落在AD上的点C处,折痕DE交BC于点E,连结C′E.
4、(2007云南双柏)如图,在梯形纸片ABCD中,AD//BC,AD>CD,将纸片沿过点D的直线折叠,使点C落在AD上的点C处,折痕DE交BC于点E,连结C′E.
求证:四边形CDC′E是菱形.
证明:根据题意可知 ![]()
则 ![]()
∵AD//BC ∴∠C′DE=∠CED
∴∠CDE=∠CED ∴CD=CE
 ∴CD=C′D=C′E=CE ∴四边形CDC′E为菱形
∴CD=C′D=C′E=CE ∴四边形CDC′E为菱形
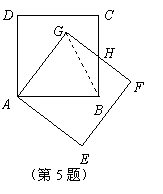
5、(2007浙江台州)把正方形![]() 绕着点
绕着点![]() ,按顺时针方向旋转得到正方形
,按顺时针方向旋转得到正方形![]() ,边
,边![]() 与
与![]() 交于点
交于点![]() (如图).试问线段
(如图).试问线段![]() 与线段
与线段![]() 相等吗?
相等吗?
请先观察猜想,然后再证明你的猜想.
 解:
解:![]() .
.
证法1:连结![]() ,
,
![]() 四边形
四边形![]() ,
,![]() 都是正方形.
都是正方形.
![]()
![]() .
.
由题意知![]() ,又
,又![]() .
.
![]() ,
,
![]() .
.
证法2:连结![]() .
.
![]() 四边形
四边形![]() 都是正方形,
都是正方形,
![]() .
.
由题意知![]() .
.
![]() .
.
![]() .
.
![]() .
.
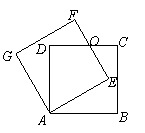
6、(2007江苏扬州)如图,正方形![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 后得到正方形
后得到正方形![]() ,边
,边![]() 与
与![]() 交于点
交于点![]() .
.
(1)以图中已标有字母的点为端点连结两条线段(正方形的对角线除外),要求所连结的两条线段相交且互相垂直,并说明这两条线段互相垂直的理由;
(2)若正方形的边长为![]() ,重叠部分(四边形
,重叠部分(四边形![]() )的面积为
)的面积为![]() ,求旋转的角度
,求旋转的角度![]() .
.
 解:(1)我连结的两条相交且互相垂直的线段是______和______.
解:(1)我连结的两条相交且互相垂直的线段是______和______.
理由如下:
(2)
(1)![]()
证明:![]() 在
在![]() 与
与![]() 中,
中,![]() ,
,
![]() ,
,
![]() (即
(即![]() 平分
平分![]() )
)
![]() (等腰三角形的三线合一)
(等腰三角形的三线合一)
注:其它的结论也成立如![]() .
.
(2)![]()
![]() 四边形
四边形![]() 的面积为
的面积为![]() ,
,
![]() 三角形
三角形![]() 的面积
的面积![]() ,
,
![]() ,
,![]() .
.
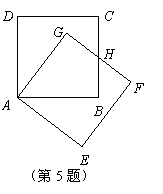
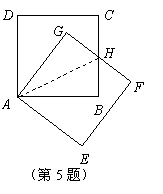
7、(2007甘肃陇南)四边形ABCD、DEFG都是正方形,连接AE、CG.
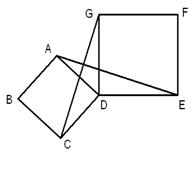 (1)求证:AE=CG;
(1)求证:AE=CG;
(2)观察图形,猜想AE与CG之间的位置关系,
并证明你的猜想.
(1) 证明: 如图,
∵ AD=CD,DE=DG,∠ADC=∠GDE=90o,
 又 ∠CDG=90o
+∠ADG=∠ADE,
又 ∠CDG=90o
+∠ADG=∠ADE,
∴ △ADE≌△CDG. ∴ AE=CG.
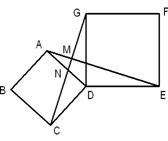
(2)猜想: AE⊥CG.
证明: 如图,
设AE与CG交点为M,AD与CG交点为N.
∵ △ADE≌△CDG, ∴ ∠DAE=∠DCG.
又∵ ∠ANM=∠CND, ∴ △AMN∽△CDN.
∴ ∠AMN=∠ADC=90o.∴ AE⊥CG.
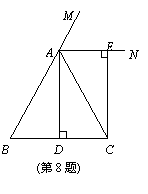 8、(2007淄博)已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
8、(2007淄博)已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形
ADCE是一个正方形?并给出证明.
(1)证明:在△A BC中, AB=AC,AD⊥BC.
∴ ∠BAD=∠DAC. ………………………………1分
∵ AN是△ABC外角∠CAM的平分线,
∴ ![]() .…………………………………………2分
.…………………………………………2分
∴ ∠DAE=∠DAC+∠CAE=![]() 180°=90°.……………3分
180°=90°.……………3分
又 ∵ AD⊥BC,CE⊥AN,
∴ ![]() =90°, ………………………………4分
=90°, ………………………………4分
∴ 四边形ADCE为矩形. ………………………………5分
(2)说明:给出正确条件得1分,证明正确得2分.
例如,当AD=![]() 时,四边形ADCE是正方形.…………6分
时,四边形ADCE是正方形.…………6分
证明:∵ AB=AC,AD⊥BC于D.
∴ DC=![]() . ………………………………………7分
. ………………………………………7分
又 AD=![]() ,∴ DC=AD.
,∴ DC=AD.
由(1)四边形ADCE为矩形,
∴ 矩形ADCE是正方形.
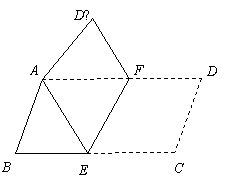 9、(2007山东青岛)将平行四边形纸片ABCD按如图方式折叠,使点C与A重合,点D落到D′ 处,折痕为EF.
9、(2007山东青岛)将平行四边形纸片ABCD按如图方式折叠,使点C与A重合,点D落到D′ 处,折痕为EF.
(1)求证:△ABE≌△AD′F;
(2)连接CF,判断四边形AECF是什么特殊四边形?证明你的结论.
证明:⑴ 由折叠可知:∠D=∠D′,CD=AD′,∠C=∠D′AE.
∵四边形ABCD是平行四边形,
∴∠B=∠D,AB=CD,∠C=∠BAD.………2′
∴∠B=∠D′,AB=AD′,
∠D′AE=∠BAD,即∠1+∠2=∠2+∠3.
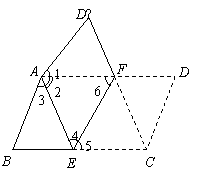 ∴∠1=∠3.
∴∠1=∠3.
∴△ABE ≌△A D′F. ……………4′
⑵ 四边形AECF是菱形.
由折叠可知:AE=EC,∠4=∠5.
∵四边形ABCD是平行四边形,∴AD∥BC.
∴∠5=∠6.∴∠4=∠6.∴AF=AE.
∵AE=EC, ∴AF=EC.
又∵AF∥EC,
∴四边形AECF是平行四边形.
∵AF=AE,
∴四边形AECF是菱形.
10、(2007四川资阳)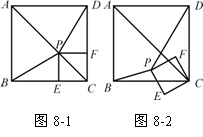 如图8-1,已知P为正方形ABCD的对角线AC上一点(不与A、C重合),PE⊥BC于点E,PF⊥CD于点F.
如图8-1,已知P为正方形ABCD的对角线AC上一点(不与A、C重合),PE⊥BC于点E,PF⊥CD于点F.
(1) 求证:BP=DP;
(2) 如图8-2,若四边形PECF绕点C按逆时针方向旋转,在旋转过程中是否总有BP=DP?若是,请给予证明;若不是,请用反例加以说明;
(3) 试选取正方形ABCD的两个顶点,分别与四边形PECF的两个顶点连结,使得到的两条线段在四边形PECF绕点C按逆时针方向旋转的过程中长度始终相等,并证明你的结论 .
⑴ 解法一:在△ABP与△ADP中,利用全等可得BP=DP.
解法二:利用正方形的轴对称性,可得BP=DP.
⑵ 不是总成立 .当四边形PECF绕点C按逆时针方向旋转,点P旋转到BC边上时,DP >DC>BP,此时BP=DP不成立.
说明:未用举反例的方法说理的不得分.
⑶ 连接BE、DF,则BE与DF始终相等.
在图8-1中,可证四边形PECF为正方形,
在△BEC与△DFC中,可证△BEC≌△DFC .
从而有 BE=DF
11、(2007南充)如图, 等腰梯形ABCD中,AB=15,AD=20,∠C=30º.点M、N同时以相同速度分别从点A、点D开始在AB、AD(包括端点)上运动.
(1)设ND的长为x,用x表示出点N到AB的距离,并写出x的取值范围.
(2)当五边形BCDNM面积最小时,请判断△AMN的形状.


解:(1)过点N作BA的垂线NP,交BA的延长线于点P. ………………(1分)
由已知,AM=x,AN=20-x.
∵ 四边形ABCD是等腰梯形,AB∥CD,∠D=∠C=30º,
∴ ∠PAN=∠D=30º.
在Rt△APN中,PN=ANsin∠PAN=![]() (20-x),
(20-x),
即点N到AB的距离为![]() (20-x). ………………………………(3分)
(20-x). ………………………………(3分)
∵ 点N在AD上,0≤x≤20,点M在AB上,0≤x≤15,
∴ x的取值范围是 0≤x≤15. ………………………………(4分)
(2)根据(1),S△AMN=![]() AM•NP=
AM•NP=![]() x(20-x)=
x(20-x)=![]() . ……(5分)
. ……(5分)
∵ ![]() <0,∴ 当x=10时,S△AMN有最大值. …………………………(6分)
<0,∴ 当x=10时,S△AMN有最大值. …………………………(6分)
又∵ S五边形BCDNM=S梯形-S△AMN,且S梯形为定值,
∴ 当x=10时,S五边形BCDNM有最小值. …………………………(7分)
当x=10时,即ND=AM=10,AN=AD-ND=10,即AM=AN.
则当五边形BCDNM面积最小时,△AMN为等腰三角形. …………(8分)


12、(2007福建福州)为创建绿色校园,学校决定对一块正方形的空地进行种植花草,现向学生征集设计图案.图案要求只能用圆弧在正方形内加以设计,使正方形和所画的图弧构成的图案,既是轴对称图形又是中心对称图形.种植花草部分用阴影表示.请你在图③、图④、图⑤中画出三种不同的的设计图案.
提示:在两个图案中,只有半径变化而圆心不变的图案属于同一种,例如:图①、图②只能算一种.
 |
解:以下为不同情形下的部分正确画法,答案不唯一.(满分8分)
 |
13、(2007福建晋江)如图,四边形ABCD为矩形,AB=4,AD=3,动点M、N分别从D、B同时出发,以1个单位/秒的速度运动,点M沿DA向终点A运动,点N沿BC向终点C运动。过点N作NP⊥BC,交AC于点P,连结MP。已知动点运动了![]() 秒。
秒。
⑴请直接写出PN的长;(用含![]() 的代数式表示)
的代数式表示)
⑵若0秒≤![]() ≤1秒,试求△MPA的面积S与时间
≤1秒,试求△MPA的面积S与时间![]() 秒的函数关系式,利用函数图象,求S的最大值。
秒的函数关系式,利用函数图象,求S的最大值。
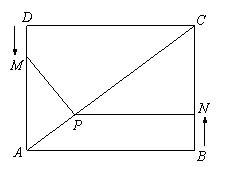 ⑶若0秒≤
⑶若0秒≤![]() ≤3秒,△MPA能否为一个等腰三角形?若能,试求出所有
≤3秒,△MPA能否为一个等腰三角形?若能,试求出所有![]() 的对应值;若不能,试说明理由。
的对应值;若不能,试说明理由。
解:⑴![]() ;
;
⑵延长NP交AD于点Q,则PQ⊥AD,由⑴得:PN=![]() ,
,
则![]() 。
。
依题意,可得:![]()
![]()
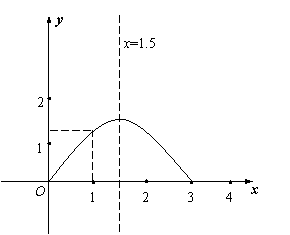 ∵0≤
∵0≤![]() ≤1.5
≤1.5
即函数图象在对称轴的左侧,函数值S
随着![]() 的增大而增大。
的增大而增大。
∴当![]() 时,S有最大值 ,S最大值=
时,S有最大值 ,S最大值=![]() 。
。
⑶△MPA能成为等腰三角形,
共有三种情况,以下分类说明:
①若PM=PA,
∵PQ⊥MA ∴MQ=QA=![]()
又DM+MQ+QA=AD ∴![]() ,即
,即![]()
②若MP=MA,则MQ=![]() ,PQ=
,PQ=![]() ,MP=MA=
,MP=MA=![]()
在Rt△PMQ中,由勾股定理得:![]()
∴![]() ,解得:
,解得:![]() (
(![]() 不合题意,舍去)
不合题意,舍去)
③若AP=AM,
由题意可得:![]() ,AM=
,AM=![]()
∴![]() ,解得:
,解得:![]()
综上所述,当![]() ,或
,或![]() ,或
,或![]() 时,△MPA是等腰三角形。
时,△MPA是等腰三角形。