中考数学模拟试题42
班级：_________ 姓名：_________ 得分：_________
一、填空题(每小题3分，共15分)
1．若∠A是锐角，且sinA＝cosA，则∠A的度数是______．
2．设方程x2-mx-1＝0的两根为x1、x2，若x1-x2＝3，则m＝______．
3．在锐角△ABC中，若sinA-
＋cosB-
＝0，则∠C＝______．
4．已知圆锥的高为4厘米，底面半径为3厘米，则此圆锥的侧面积为______平方厘米．(结果中保留p )
5．已知M、N两点关于y轴对称，且点M在双曲线y＝
上，点N在直线y＝x＋3上，设点M坐标为(a，b)，则抛物线y＝-abx2＋(a＋b)x的顶点坐标为______．
二、选择题(每小题3分，共18分)
6．若函数y＝
的自变量x的取值范围为一切实数，则m的取值范围是( )
A．m≤1 B．m＝1 C．m＞1 D．m＜1
7．如果一组数据a1，a2，…an的方差是2，那么一组新数据3a1，3a2，…3an的方差是( )
A．2 B．6 C．12 D．18
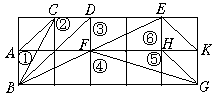
8．如图1中的5个半圆，邻近的两半圆相切，两只小虫同时出发，以相同的速度从A点到B点，甲沿ADA1、A1EA2、A2FA3、A3GB路线爬行，乙虫沿ACB路线爬行，则下列结论正确的是( )
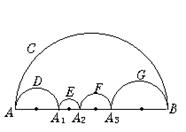
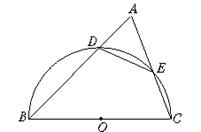
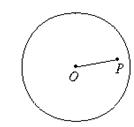
图1 图2 图3
A．甲先到B点; B．乙先到B点 C．甲乙同时到达B点; D．无法确定
9．如图2，锐角△ABC中，以BC为直径的半圆O分别交AB、AC于D、E两点，且
S△ADE∶ S四边形DBCE＝1∶2，则cosA的值是( )
A． B．
C．
D．
10．如图3，点P是半径为5的⊙O内一点，且OP＝3，在过点P的所有⊙O的弦中，弦长为整数的弦的条数为( )
A．2 B．3 C．4 D．5
11．某种商品进价为800元，出售时标价为1200元，后来由于该商品积压，准备打折出售，要保持利润率不低于5%，该商店至多可打( )
A．6折 B．7折 C．8折 D．9折
三、解答题(12～16每小题7分，共35分)
12．一次函数y＝kx＋b表示的直线经过点A(1，-1)、B(2，-3)，请你判断点P(0，1)是否在直线AB上，并说明你的理由．
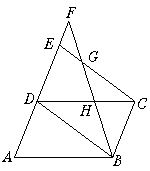
13．如图，在平行四边形ABCD的边AD的延长线上截取DE＝AD，F是AE延长线上的一点，连结BD、CE、BF分别交CE、CD于G、H．
求证：(1)△ABD≌△DCE； (2)CE∶CG＝DF∶AD．
14．若关于x的一元二次方程3x2＋3(a＋b)x＋4ab＝0的两个实数根x1、x2满足关系式：
x1(x1＋1)＋x2(x2＋1)＝(x1＋1)(x2＋1)．
判断(a＋b)2≤4是否正确，若正确，请加以证明；若不正确，请举一反例．
15．如图，在正方形网格上有6个斜三角形：①△ABC，②△CDB，③△DEB，④△FBG，⑤HGF，⑥△EKF．请你写出与△ABC相似的三角形，并写出简要的证明．
16．如图，距沿海某城市A正南220千米的B处，有一台风中心，其最大风力为12级，每远离台风中心20千米，风力就减弱1级，该中心正以每小时15千米的速度沿北偏东30°的BC方向移动，且风力不变，若城市A所受风力达到或超过4级，则称为受台风影响．
(1)A城市是否会受台风影响？为什么？
(2)若会，将持续多长时间？
(3)该城市受台风影响的最大风力为几级？
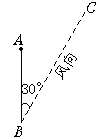
四、解答题(每题8分，共32分)
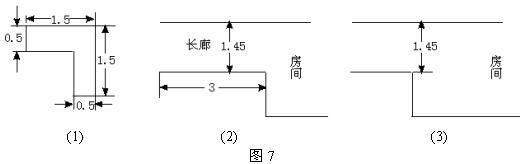
17．如图(1)所示是某立式家具(角书橱)的横断面，请你设计一个方案(角书橱高2米，房间高2.6米，所以不必从高度方面考虑方案的设计)，按此方案，可使该家具通过图(2)中的长廊搬入房间．在图(3)中把你设计的方案画成草图，并说明按此方案可把家具搬入房间的理由(注：搬运过程中不准拆卸家具，不准损坏墙壁)．
18．已知二次函数y＝mx2＋4x＋2．
(1)若函数图象与x轴只有一个交点，求m的值；
(2)是否存在整数m，使函数图象与x轴有两个交点，且两交点横坐标差的平方等于8？若存在，求出符合条件的m值；若不存在，请说明理由．
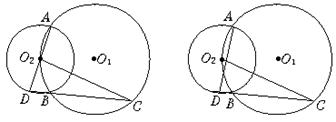
19．已知：⊙O1与⊙O2相交于A、B两点，且O2在⊙O1上(如图8)
(1)AD是⊙O2的直径，连DB并延长交⊙O1于点C，求证：CO2⊥AD．
(2)若AD是⊙O2的非直径的弦，直线DB交⊙O1于点C，则(1)中的结论是否成立，为什么？请加以证明．
20．已知：在内角不确定的△ABC中，AB＝AC，点E、F分别在AB、AC上，EF∥BC，平行移动EF，如果梯形EBCF有内切圆．
当
＝时，sinB＝
；
当＝时，sinB＝(提示：＝
)；当＝
时，sinB＝
．
(1)请你根据以上所反映的规律，填空：当＝
时，sinB的值等于______；
(2)当＝
时(n是大于1的自然数)，请用含n的代数式表示sinB＝______，并画出图形、写出已知、求证和证明过程．
参考答案
一、1．45° 2．
3．60° 4．15p
5．利用对称性，可有N(-a，b)，易求得2ab＝1，a＋b＝3．
故y＝-x2＋3x，其顶点坐标为(3，
)．
二、6．C 7．D 8．C 9．D 10．C 11．B
三、12．解：由题意得
解得：
得直线AB的解析式为y＝-2x＋1，
将点P(0，1)代入后满足解析式说明点P(0，1)在直线AB上．
13．(1)先证四边形DBCE为平行四边形，则CE平行且等于DB．
且∠ADB＝∠DEC，AD＝BC＝DE．
所以△ABD≌△DCE．
(2)由△DBF∽△GBC，可得
，
又因为CE＝DB，CB＝AD，所以
．
即CE∶CG＝DF∶AD．
14．∵ 关于x的一元二次方程3x2＋3(a＋b)x＋4ab＝0有两个实数根，
∴ Δ≥0，即［3(a＋b)2］-4 4ab≥0，
3(a＋b)2-16ab≥0 ①
∵ x1、x2为方程的两个实数根，
∴ x1＋x2＝-(a＋b)，x1·x2＝
．
∵ x1(x1＋1)＋x2(x2＋1)＝(x1＋1)(x2＋1)，
∴ x12＋x1＋x22＋x2＝x1x2＋x1＋x2＋1，
x12＋x22＝x1x2＋1，
(x1＋x2)2-3x1x2＝1．
∴ ［-(a＋b)］2-3＝1，
(a＋b)2-4ab＝1
∴ 4ab＝(a＋b)2-1 ②
把②代入①，得
3(a＋b)2-4［(a＋b)2-1］≥0，
∴ (a＋b)2≤4．
15．△DEB∽△FBG∽△HGF∽△ABC．证略．
16．解：(1)会受到影响，距台风中心160千米就会受到影响．
而A城到台风路线BC距离为110千米．
(2)4
小时
(3)最大风力6.5级．
四、17．解：如下图，角书橱ABCDE，作AM⊥CD，垂足为M，
可知△AFM是等腰直角三角形．
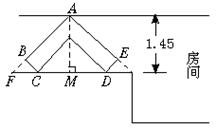
∴ AM＝FM．
而AF＝AB＋BF＝AB＋BC＝1.5＋0.5＝2(米)，
∴ AM＝AFsin45°＝2·＝
(米)．
∵ 米＜1.45米，故可按方案把家具搬入房间．
18．解：(1)由题意得，Δ＝16-8m＝0，得m＝2．
(2)若存在符合条件的m值，可设函数图解与x轴的两个交点横坐标为x1、x2，则
x1＋x2＝-
，x1x2＝
，
∴ (x1-x2)2＝(x1＋x2)2-4x1x2＝
-
＝8，
即
＝8
解得m＝1或m＝2，都使得Δ＞0，
∴ 所求的m值为1，-2．
19．(1)连结AB，
∵ AD是⊙O2的直径，
∴ ∠ABD＝90°，得∠A＋∠D＝90°．
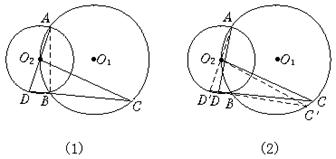
又∵ ∠C＝∠A＝
，
∴ ∠C＋∠D＝90°，
得∠CO2D＝90°，即CO2⊥AD．
(2)(1)中的结论仍成立．证明如下：
连结直径AO2交⊙O2于点D′，连D′B并延长交⊙O1于点C′，连O2C′．
由(1)知C′O2⊥AD′ ①
又∠A＝∠DBD′＝
，
∠DBD′＝∠CBC′，
∠CBC′＝∠CO2C′＝
②
得∠A＝∠COC′
由①②可得：CO2⊥AD．
20．(1)
(2)
．
已知：在△ABC中，AB＝AC，EF∥BC，⊙O内切于梯形EBCF，点D、N、G、M为切点，
(n是大于1的自然数)，如下图．
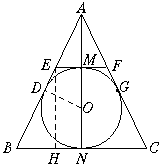
求证：sinB＝
．
证明：连结AO并延长与BC相交．
∵ ⊙O内切于梯形EBCF，AB、AC是⊙O的切线，
∴ ∠BAO＝∠CAO．
∵ EF∥BC，AB＝AC，∴ AE＝AF．
又M、N为切点，∴ OM⊥EF，ON⊥BC．
∴ AO⊥EF于M，AO⊥BC于N．
∵ EF∥BC，∴ EM∥BN．
∴ △AEM∽△ABN．∴ 
．
设EM＝k，则BN＝nk．
作EH∥MN交BC于H，则HN＝EM＝k．
∵ D、N、M为切点，∴ BD＝BN＝nk，ED＝EM＝k．
在△EHB中，∠EHB＝∠MNB＝90°，
BE＝BD＋DE＝(n＋1)k，
BH＝BN-HN＝(n-1)k．
由勾股定理，得EH＝2
·k．
∴ sinB＝
．