二 空间与图形
第四单元 图形的认识
第17课 相交线与平行线
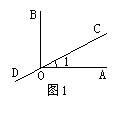
1．如图1，已知OB⊥OA，直线CD经过O点，∠AOC=35°，则∠DOB的度数是 ．
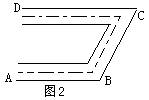
2．如图2，所示，一个合格的弯形管道经两次拐弯后，如果∠C=68°，∠B=112°，则AB与CD的位置关系是 ．
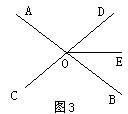
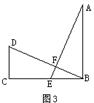
3．如图3，直线AB、CD相交于O，已知∠AOC=80°，OE把∠BOD分成两个角，且
∠BOE∶∠EOD=3∶5，则∠EOD= ．
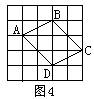
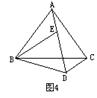
4．如图4，线段AB是由线段CD向左平移 格，并向上平移 ．格后得到的．
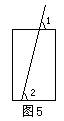
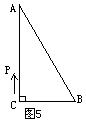
5．如图5，用吸管吮吸易拉罐内的饮料时，吸管与易拉罐上部的夹角为∠1=78°，那么吸管与易拉罐下部的夹角∠2= 度．
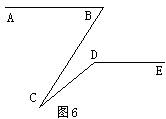
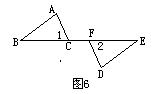
6．如图6，∠ABC=81°，∠CDE=133°，当∠BCD= 时，AB∥DE．
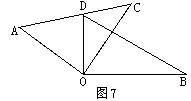
7．如图7，将一副三角板叠在一起，使直角顶点重合于点O，OC⊥DB，则∠AOB+∠DOC= ．
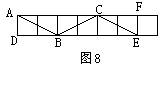
8．在中国象棋中，马走“日”字，如图8，若棋盘上每个小方格的边长都是5cm的正方形，“马”连跳三步从A到E，那么两平行直线AD与EF间的距离是 ．
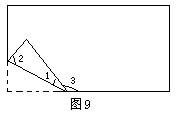
9．如图9所示，把长方形纸片的一个角折过去，则∠1+∠2= ．
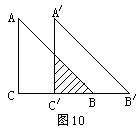
10．如图10，在直角△ABC中，∠C=90°，BC=8cm，AC=8cm，现将△ABC沿CB方向平移到△A′B′C′的位置，如果平移距离为4cm，则阴影部分的面积为 ．
11．下面是几个生活中产生的现象：
⑴用两个钉子就可以把木条固定在墙上
⑵植树时，只要定出两棵树的位置，就能确定同一行树所在的直线
⑶从A地到B地架设电线总是尽可能沿着线段AB架设
⑷把弯曲的公路修直就能缩短路程
其中，可以用“两点之间，线段最短”来解释的现象为（ ）
A ⑴⑵ B ⑴⑶ C ⑵⑷ D ⑶⑷
12．a、b、c是平面上任意三条直线，它们的交点的个数可能有（ ）
A．1个或2个 B．1个或2个或3个
C．0个或1个或2个或3个 D．0个或1个或2个
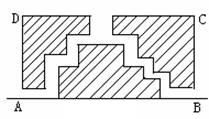13．如图11是一块长方形的场地，长AB=103米，宽AD=51米，A、B两处入口的路宽都为1米，两小路汇合处路宽为2米，其余部分种植草坪，则草坪的面积为（ ）
A．5050平方米 B．4900平方米
C．5000平方米 D．4998平方米
|
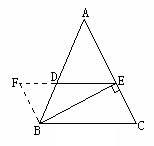⑵过点B做BF∥AC，交ED的延长线与点F，求∠BFE的度数．
|
15．先解答问题⑴，再探索⑵⑶⑷的结论．
如图13所示，已知：∠AOB是直角，∠BOC=30°，OM平分∠AOC，ON平分∠BOC；
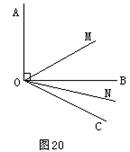⑴求∠MON的度数；
⑵若∠AOB=a，其他条件不变时，∠MON= ．
⑶若∠BOC=β，其他条件不变时，∠MON= ．
⑷分析⑴⑵⑶的结果及你解答的过程，可以看出∠MON= ．
|
16．在同一平面内的三条直线能把该平面分成几部分？请画出相应的图形，如果
是n条直线，它们最多把平面分成几部分？
第18课 三角形的概念
1．已知△ABC的周长是偶数，且a=2，b=5，则此三角形的周长是 ．
2．一个正多边形的内角和是1440°，则此多边形的边数是 ．
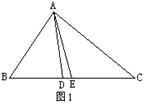
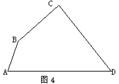
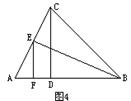
3．如图1，AD、AE分别是△ABC的角平分线和中线，如果∠BAD=44°， CE=6cm，那么∠BAC= ；BC= ．
4．在△ABC中∠A+∠B=130°，∠C=2∠A，则∠A= ；∠B= ．
5．一个多边形的内角和与外角和的差是180°，则这个多边形的边数为 ．
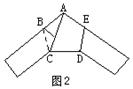
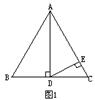
6．用一条宽度相等的足够长的纸条，打一个结，然后轻轻拉紧，压平就可以得到如图2所示的正五边形ABCDE，其中∠BAC= 度．
7．若△ABC三边长为整数，周长为11，且有一边长为4，则这个三角形的最大边长是 ．
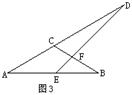
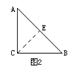
8．如图3，∠A=27°，∠BFE=95°，∠B=38°，则∠D= ．
9．一个多边形只截去一个角，形成另一个多边形的内角和为2520°，则原多边形的边数为 （截线不经过顶点）．
10．用三块正多边形的瓷砖铺地，拼在一起，并相交于一点的各边完全吻合，若其中两块瓷砖的边数均为五边形，则第三块瓷砖为正
边形．
11．如图4，AB、BC、CD是三根长度分别为1cm、2cm、5cm的
木棒，现在A、D之间拉一根橡皮筋，请根据四边形的不稳定性 ，思考这根橡皮筋的最大长度可拉到 ，最短长度可为 ．
12．如果三角形的三边长是三个连续自然数，则下列判断错误的是（ ）
A．周长大于6 B．周长可以被6整除
C．周长可以被3整除 D．周长有时是奇数
13．下列条件：⑴∠A+∠B=∠C；⑵∠A∶∠B∶∠C=1∶2∶3；⑶∠A=90°—∠B；⑷
∠A=∠B=
∠C；⑸∠A=2∠B=3∠C，其中能确定△ABC是直角三角形的条件有（ ）
A．2个 B．3个 C．4个 D．5个
14．在直角三角形中，两锐角平分线相交成钝角的度数是（ ）
A．90° B．100° C．135° D．150°
15．以线段a=3，b=4，c=5，d=6为边做四边形，这样的四边形能作（ ）
A．1个 B．2个 C．4个 D．无数个
16．若等腰三角形一腰上的高等于其腰长的一半，则这个等腰三角形的顶角为（ ）
A．30° B．150° C．120° D．30°或150°
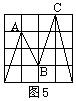
17．如图5，在4×4正方形网格中，∠A、∠B、∠C的大小关系是（ ）
A．∠A>∠B>∠C B．∠A=∠B=∠C
C．∠A<∠B>∠C D．∠A=∠B>∠C
18．锐角三角形中，最大角的取值范围是（ ）
A．0°<a<90° B．60°<a<90° C．60°<a<180° D．60°≤a<90°
19．已知一个三角形形状的零件的三边长都是整数，并且唯一最长边是7，这样的三角形零件共有（ ）
A．6种 B．7种 C．8种 D．9种
20．一个多边形，每个内角的度数都等于150°，求这个多边形的内角和．
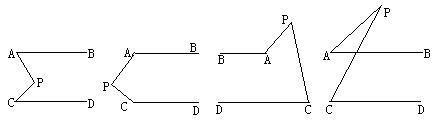21．如图6，AB∥CD，分别探讨下面四个图形中∠APC与∠PAB、∠PCD的关系，请你从所得到的关系中任选一个加以说明．
|
22．有边数分别为x、y、z的型号不同的多边形，且每种型号的多边形均满足各边相等，各角相等．如果每种型号的多边形各取一个，拼在A点，恰好能覆盖A点及其周围小区域，请你提出一个关于x、y、z之间的关系的猜想，并加以证明．
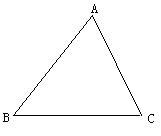
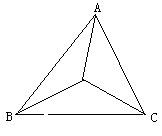
23．某校的一块三角形空地（如图7）需要绿化，拟从点A出发，将△ABC分成面积相等的4个三角形，以便种上四种不同的花草，请你帮助画出规划图案．
|
|
|
第19课 全等三角形(含全等三角形、等腰三角形)
1．如图1，△ABD≌△AEC,且AB=AE,则BD、AD的对应边分别是 ．
2． 如图2，△ABC≌△ADE ,∠EAC=30°，则∠BAD= ．
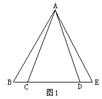
3．如图3，AB⊥BC，CD⊥BC，垂足分别为B，C．AB=BC，E为BC中点，且AE⊥BD与F，若CD=4cm，则AB的长度为 ．
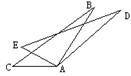
4．如图4，点E在AD上 ，△ABC和△BDE都是等边三角形，则∠ADC的度数是 ．
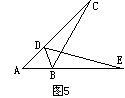
5．如图5，已知点D在AC上，点 B在AE上，△ABC≌△DBE，∠BDA=∠A，∠A∶∠C=5∶3，则∠DBC的度数 ．
|
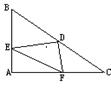
6．如图6，∠1=∠2，BC=EF，那么需要补充一个直接的条件 （写出一个即可）才能使△ABC≌△DEF．
7．在Rt△ABC中，∠C=90°，AD平分∠BAC交BC于点D，若CD=4，则点D到斜边AB的距离等于 ．
8．如图7，已知在△ABC中，AB=AC，∠A=90°，D是斜边BC的中点，E，F分别是AB，AC边上的点，且DE⊥DF，若BE=7，CF=5，则 AE= ，AF= ．
9．如图8，AD平分∠BAC，AB=AC，则图中有多少对全等三角形（ ）．
A．2 B．4 C．4 D．5
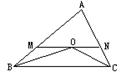
10．如图9，在△ABC中，BO平分∠ABC，CO平分∠ACB，MN∥BC，MN经过点O，若AB=10cm,AC=18cm，则△AMN的周长是（ ）
A．10 cm B．18 cm C．24 cm D．28cm
|
| ||||||
| |||||||
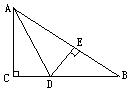
11．如图10，AC⊥BC，AD平分∠BAC，DE⊥AB于E，下列结论⑴AD平分∠CDE；⑵∠BDE=∠BAC；⑶DE平分∠ADB；⑷AC+BE=AB，其中正确的有（ ）个
A．1 B．2 C．3 D．4
12．已知AD平分∠BAC交BC于点D，自点D向AB、AC两边或其延长线作垂线，垂足分别是E、F，那么下列结论中错误的是（ ）
A．DE=DF B．AE=AF C．BD=DC D．∠ADE=∠ADF
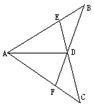
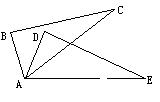13．如图11，△ABC≌△ADE，∠B=70°，∠C=26°，∠DAC=30°， 则∠EAC的度数为（ ）
A．27° B．54° C．30° D．55°
|
并证明全等．
|
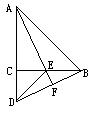
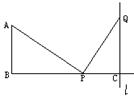15．如图13，AB=2，BC=5，AB⊥BC于B，l⊥BC于C，点P自点B开始沿射线BC移动，点Q在直线l上移动，且∠APQ=90°．
⑴求证：∠A=∠QPC；
⑵当点P运动到何处时，PA=PQ？并说明理由．
|
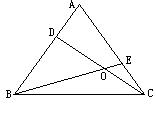
16．如图14，小李分别在等边△ABC的边AB、AC上取点D、E，量得AD=CE，连接BE、CD交于点O，于是，他发现了下面的结论：
⑴BE与CD一定相等；
⑵只要点D、E分别在边AB、AC上（不与点A、B、C重合）且AD=CE，那么∠COD的大小就始终不变，你认为他的发现正确吗？请分别加以说明.
|
第20课 特殊三角形的性质（含勾股定理，等腰三角形）
1．等腰三角形的一个角为50°，那么它的一个底角为 ．
2．如图1，在等边△ABC中，AD⊥BC，DE⊥AC，垂足分别是D、E，则CE：AE= ．
3．等腰三角形的两边长分别为5㎝和2㎝，则其周长为 ．
4．如图2，在Rt△ABC中，E是斜边AB上一点，把△ABC沿CE折叠，点A与点B恰好重合，如果AC=4㎝，那么AB= ．
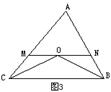
5．如图3，在△ABC中BO平分∠ABC，CO平分∠ACB，MN∥BC，MN 经过点O，AB=12，AC=18，那么△ABC的周长是
．
6．图4，在△ABC中，CD是AB边上的高，BE是AC边上的中线，
EF⊥AB，垂足为F，若∠ABE=30°BE=2，则CD= ．
7．
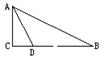图5，在Rt△ABC中，∠C=90°，BC=6㎝，CA=8㎝，动点P从点C出发，以2㎝/s的速度沿CA、AB移动到点B，则P点出发_____秒，可使S△BCP=S△ABC．
|
A．2 B．4 C．3 D． 6
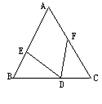
9．如图7，在△ABC中，AB=AC，且BD=CF，∠A=40°，
则∠EDF=( )
A．
|
10．已知，如图8，在等边三角形ABC中，BD=CE，AD与BE相交于点P，则∠APB的度数为( )
A. 45° B. 55° C. 60° D. 75°
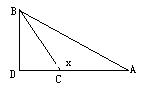
11．如图9，在Rt△ABC中，∠D=90°，C为AD上一点，则x可能是( )
A．10° B．20° C．30° D．40°
|
| ||||||
| |||||||
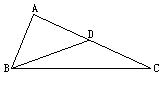
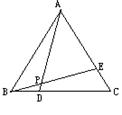
12．如图10，在△ABC中，D是AC上一点，且AD=DB=DC，∠C=40°，你能求出∠ABD的度数吗？请写出过程．
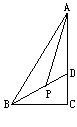
13．如图11，已知在直角三角形中，∠C=90°，BD平分∠ABC且交AC于D．
⑴若∠BAC=30°，求证：AD=BD；
|
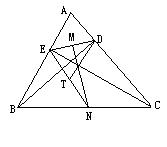14．如图12，已知在锐角三角形ABC中，BD、CE分别为AC、AB边上的高，垂足分别为D、E，连接ED，M、N点分别为ED、BC的中点
⑴MN与ED有什么特殊的位置关系？
⑵连接EN，取EN的中点T，当DT垂直于EN时，求∠A的度数．
|
15．正三角形给人以“稳如泰山”的美感，它具有特殊的对称性，⑴请你用三种不同的分割方法，将正三角形分别分割成四个等腰三角形；⑵怎样把正三角形分割成5个等腰三角形．
第21课 平行四边形
1．在平行四边形ABCD中，∠C＝∠B+∠D,则∠A＝ ，∠D＝ ．
2．在平行四边形ABCD中，已知对角线AC和BD相交于点O，△ABO的周长为15，AB＝6，那么对角线AC＋BD＝ ．
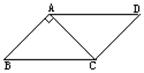
3．如图，已知O是□ABCD的对角线交点，AC＝24，BD＝38，AD＝14，那么△OBC的周长等于 ．
4．如图,已知平行四边形ABCD中,AB=AC,AB⊥AC,A到BC的距离为1厘米.那么平行四边形ABCD的周长 ．
5
第3题图 第4题图
5．在平面直角坐标系中，点A、B、C的坐标分别是A(－2，5)，B(－3，－1)，C(1，－1)，在第一象限内找一点D，使四边形ABCD是平行四边形，那么点D的坐标是 ．
6．在平行四边形ABCD中，AE⊥BC于E，AF⊥CD于F，若AE=4,AF=6,平行四边形的周长为40，则
ABCD = ．
7．用两块全等的含有30°角的三角板拼成形状不同的平行四边形，最多可以拼成 ( )
A．1个 B．2个 C．3个 D．4个
8．在□ABCD中，∠A：∠B：∠C：∠D的值可以是（ ）
A．1：2：3：4 B．1：2：2：1
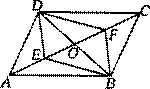
C．2：2：1：1 D．2：1：2：1 第9题图
9．如图，平行四边形ABCD中，对角线AC、BD相交于点O，E、F是AC上的两点，当E、F满足下列哪个条件时，四边形DEBF不一定是平行四边形( )
A．∠ADE＝∠CBF B．∠ABE＝∠CDF
C．OE＝OF D．DE＝BF
10．已知四边形ABCD中,AC交BD于点O,如果只给条件“AB∥CD”,那么还不能判定四边形ABCD为平行四边形,给出以下四种说法:
(1)如果再加上条件“BC=AD”,那么四边形ABCD一定是平行四边形；
(2)如果再加上条件“
”,那么四边形ABCD一定是平行四边形；
(3)如果再加上条件“AO=OC”,那么四边形ABCD一定是平行四边形；
(4)如果再加上条件“
”,那么四边形ABCD一定是平行四边形．
其中正确的说法是 ( )
A.(1)(2) B.(1)(3)(4) C.(2)(3) D.(2)(3)(4)
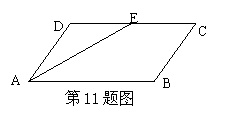11．如图，平行四边形ABCD中，∠A的平分线
AE交CD于E，AB=5，BC=3，则EC的长（ ）
A．1 B．1.5 C．2 D．3
12．在一次数学探究活动中，小强用两条直线把平行四边形ABCD分割成四个部分，使含有一组对顶角的两个图形全等．
(1)根据小强的分割方法，你认为把平行四边形分割成满足以上全等关系的直线有
组．
(2)请在下图的三个平行四边形中画出满足小强分割方法的直线．
(3)由上述实验操作过程，你发现所画的两条直线有什么规律?
13．如图, 中,DB=CD,
,AE⊥BD于E.试求
的度数.
第13题图
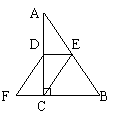14．如图，△ABC中∠ACB＝90o，点D、E分别是AC，AB的中点，点F在BC的延长线上，且∠CDF＝∠A．
求证：四边形DECF是平行四边形．
第14题图
第22课 特殊的平行四边形
1．正方形的边长为4cm，则周长为 ，面积为 ．
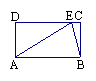
2．已知：如图所示，E为正方形ABCD外一点，AE＝AD，∠ADE＝75°，则∠AEB＝ ．
（第2题） （第4题） （第7题） （第8题）
3．菱形的周长为20cm，相邻内角度数之比为2∶1，则菱形较短的对角线长为 cm．
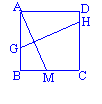
4．已知：矩形ABCD中，AB＝2CB，点E在DC上，且AE＝AB，则∠EBC＝ ．
5．正方形ABCD中，对角线的长是10cm，点P是AB上任意一点，则点P到AC、BD的距离之和是 ．
6．在正方形ABCD中，E、F、G、H分别是边AB、BC、CD、DA的中点，则四边形EFGH是 形．
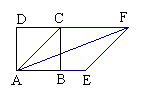
7．如图所示不，在正方形ABCD中，M是BC上一点，连结AM，作AM的垂直平分线GH交AB于G，交CD于H，若AM＝10cm，则GH＝ ．
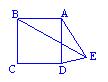
8．以正方形ABCD的对角线AC为一边作菱形AEFC，则∠FAB＝ ．
9．在四边形ABCD中，O是对角线的交点，下列条件能判定这个四边形是正方形的是（ ）
A．AC＝BD，AB∥CD，AB＝CD B．AD∥BC，∠A＝∠C
C．AO＝BO＝CO＝DO，AC⊥BD D．AC＝CO，BO＝DO，AB＝BC
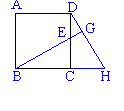10．如图所示，在正方形ABCD中，H是BC延长线上一点，使CE＝ CH，连结DH，延长BE交DH于G，则下面结论错误的是（ ）
A．BE＝DH B．∠H＋∠BEC＝90°
C．BG⊥DH D．∠HDC＋∠ABE＝90°
11．正方形具有而菱形没有的性质是（ ） （第9题）
A．对角线互相平分 B．每条对角线平分一组对角
C．对角线相等 D．对边相等
12．以线段AB的两个端点A、B为顶点作位置不同的正方形，一共可作（ ）
A．1个 B．2个 C．3个 D．4个
13．用两个形状和大小完全一样的直角三角形,一定能拼成下列图形中的
①等腰三角形;②平行四边形;③矩形;④菱形;⑤正方形. ( )
A.①②③ B.②③④ C.①③⑤ D.①②③④⑤
14．两条邻边分别是15cm和20cm的平行四边形最大面积是（ ）cm2．
A．75 B．150 C．200 D．300
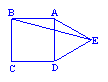15．如图所示，以正方形ABCD中AD边
为一边向外作等边ΔADE，则∠AEB＝（ ）
A．10° B．15° C．20° D．12.5°
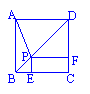16．如图所示，正方形ABCD中，P是对角线BD上一点，PE⊥BC于E，PF⊥CD于F．请猜想EF与PA的数量关系、位置关系，并说明理由．
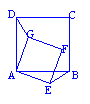17．已知：如图所示，在正方形ABCD和正方形AEFG有一个公共顶点A，把正方形AEFG绕A点旋转到如图所示位置，连结DG、BE．试说明：DG＝BE．
18．如图所示，在矩形ABCD中，AB＝24cm，BC＝12cm，点P沿AB边从点A开始向点B以2cm/s的速度移动，点Q沿DA边从点D开始向点A以1cm/s的速度移动．如果P、Q同时出发，用t(s)表示移动时间(0≤t≤12)，那么：
①当t为何值时，ΔQAP为等腰直角三角形；
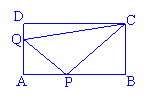②求出此时四边形QAPC的面积，并提出一个与计算结果有关的结论．
第23课 梯形
1．在梯形ABCD中，AD∥BC，∠B=72°，∠ C=48°，则∠A= ，∠D= ．
2．在梯形ABCD中，AD∥BC，过点D作AB的平行线交BC于E，若梯形周长为52cm，AD=7cm，则△CDE的周长是 ．
3．在等腰梯形ABCD中AD∥BC，∠BDC=90°，且BD平分∠ABC，∠ABC=60°，梯形的周长为a，则AD= ．
4．已知梯形的上底为2，下底为5，一腰长为4，则另一腰x的取值范围是 ．
5．梯形的两条对角线分别为17cm、10cm，高为8cm，则它的面积是 cm2．
6．等腰梯形中，已知一个底角为45°，高为h，中位线长为m，则梯形上底是 ．
7．如图，EF是△ABC的中位线，BD平分∠ABC交EF于D，若DE=2，则EB= ．
第7题图 第8题图 第11题图
8．如图，在梯形ABCD中，AD∥BC，且AD∶BC=3∶5，梯形ABCD的面积是8cm2，点M、N分别是AD和BC上的点，E、F分别是BM、CM的中点，则四边形MENF的面积是 ．
9．下列说法正确的是（ ）
A．有一组对边平行的四边形是梯形 B．一组对边平行且不相等的四边形是梯形
C．直角梯形是有两个角是直角的四边形 D．有两个角相等的梯形是等腰梯形
10．已知直角梯形的一腰长为10cm，这腰与底所成的角是60°，则另一腰的长是（ ）
A．5cm B．
cm C．2.5cm D．
cm
11．如图，在梯形ABCD中，AD∥BC，M是CD的中点，AF⊥BC于F，∠B=45°，AF=3，EF=5，则梯形ABCD的面积为（ ）
A．12 B．24 C．6 D．16
12．等腰梯形的上底与高相等，下底是上底的3倍，则下底的一个角的度数为（ ）
A．30° B．60° C．45° D．75°
13．梯形两底分别是10cm、26cm，同一底上两底角分别是60°和30°，则较短腰长是（ ）
A．8cm
B．
cm
C．12cm
D．4cm
14．梯形中位线长12cm，一条对角线把中位线分成1∶3两部分，则梯形两底分别为（ ）
A．4cm、8cm B．9cm、15cm C．10cm、14cm D．6cm、18cm
15．在梯形ABCD中AB∥CD，AD=BC，中位线EF=15cm，∠DAB=60°，AC平分∠DAB，则梯形ABCD的周长是（ ）
A．30cm B．40cm C．50cm D．60cm
16．平面上A、B两点到直线l的距离分别是
和
，则线段AB的中点C到直线l的距离是（ ）
A．3
B．
C．3或
D．6或2
17．如图，在梯形ABCD中，AB∥DC， AD=BC，延长AB到E，使BE=DC，连结AC、CE．求证：AC=CE．
18．如图，已知在梯形ABCD中，AB∥DC，∠D=60°，∠C=45°，AB=2，AD=4，求梯形ABCD的面积
19．如图，梯形ABCD中，AD∥BC，∠BCD=90°， BC=2CD，AB=BC，
求∠ACD的度数．
20．如图，在直角梯形ABCD中AD∥BC，∠B=90°，CD=BC+AD，问：在AB上是否存在一点P，使∠CPD=90°？若存在，请把这点找出来，并给予证明；若不存在，请说明理由．
第24课 圆的有关概念
1.下列命题中正确的是（ ）
A.平分弦的直线垂直于弦
B.平分弦的直线也必平分弦所对的两条弧
C.弦的垂直平分线必平分弦所对的两条弧
D.平分一条弧的直线必平分这条弧所对的弦
2.一个点到圆的最小距离为4cm，最大距离为9cm，则该圆的半径是（ ）
A.2.5 cm或6.5 cm B.2.5 cm C.6.5 cm D.5 cm或13cm
3.圆内接四边形ABCD中，∠A、∠B、∠C的度数比是2︰3︰6，则∠D的度数是（ ）
A.67.5° B.135° C.112.5° D.110°
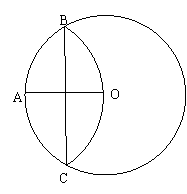
4.如图，AB为⊙O的一固定直径，它把⊙O分成上、下两个半圆，自上半圆上一点C作弦CD⊥AB，∠OCD的平分线交⊙O于点P，当点C在上半圆（不包括A、B两点）上移动时，点P（ ）
A.到CD的距离保持不变 B.位置不变
C.等分弧DB D.随C点移动而移动
5.已知⊙O的半径为10cm，弦AB∥CD，AB＝12 cm，CD＝16 cm， 则AB和CD的距离是（ ）
A.2cm B.14cm
C.2cm或14cm D.2cm或12cm
6. 在半径为5cm的⊙O中，有一点P满足OP＝3 cm，则过P的整数弦有（ ）条.
A.2 B.3 C.4 D.5
7.若
为⊙O的直径，
为⊙O的一条弦长，则与的大小关系是 ．
8.在半径为1的⊙O中，弦AB、AC的长分别为
和
，则∠BAC的度数为 ．
9.⊙O中弦AB⊥CD于E，AE＝4，EB＝6，CE＝2 ,ED＝12，则⊙O的半径为 ．
10.⊙O中，半径CO垂直于直径AB，D为OC的中点，过D作弦EF∥AB，则∠CBE＝ ．
11.AB为⊙O的直径，AC为弦，OD⊥AC于D，BD交OC于E，若AC＝4，AB＝5，则BE＝ ．
12.已知⊙O1与⊙O2相交于A、B两点，C、A、D三点在一条直线上，CD的延长线交O1 O2的延长线于P，∠P＝300，
，则CD＝ ．
13.圆内一弦与直径相交成300的角，且分直径为1 cm和5 cm两段，则此弦长为 ．
14.弧AB的度数为900，点C和点D将弧AB三等分，半径OC、OD分别和弦AB交于E、F．求证：AE＝CD＝FB．
15.在⊙O中，两弦AB与CD的中点分别是P、Q，且弧AB＝弧CD，连结PQ，
求证：∠APQ＝∠CQP．
16.在⊙O中，两弦AC、BD垂直相交于M，若AB＝6，CD＝8，求⊙O的半径．
17.已知A、B、C、D四点顺次在⊙O上，且弧AB=弧CD，BM⊥AC于M，求证：AM＝DC＋CM．
18.Rt△ABC中，∠C＝900，AC＝3，BC＝4，以点C为圆心，CA为半径的圆与AB、BC分别交于点D、E，求AB、AD的长．
19.⊙O的半径为10cm，G是直径AB上一点，弦CD经过点G，CD＝16cm，AE⊥CD于E，BF⊥CD于F，求AE－BF的值．
第25课 与圆有关的位置关系
1．已知⊙O的半径是8cm，点P到点O的距离不大于8cm，则点P在 ．
2．已知⊙O1 与⊙O2分别是6和2，圆心
的坐标是（0，8），圆心
的坐标是（－6，0），两圆的位置关系是
．
3．在
中，内切圆⊙O与边AB、BC、CA分别相切于D、E、F，
，则
．
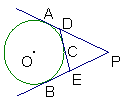
4．PA、PB切⊙O于点A、B，过圆上一点C的切线交PA、PB于点D、
E，PA=9，则
的周长= ． 第4题图
5．已知线段AB=4cm，M是AB的中点，分别以A、B为圆心，
、
为半径画圆，若点M在⊙A外，又在⊙B内，则 的范围是
，的范围为
．
6．在直角坐标系中，点A的坐标是（－3，4），以A为圆心，4为半径作圆，
（1）x轴与⊙A的位置关系是 ．（2）y轴与⊙A的位置关系是 ．
（3）原点与⊙A的位置关系是 ．
7．给出下列几种判定切线的说法：
①过直径一端的直线是圆的切线．②垂直于半径的直线是圆的切线．
③过半径的一端且垂直于半径的直线是圆的切线．
④和圆心的距离等于半径的直线是圆的切线．⑤和圆有唯一公共点的直线是圆的切线．
其中说法正确的序号是 ．
8.⊙O1 与⊙O2的半径分别是3cm和4cm，若O1 O2= 10cm，则这两个圆的位置关系为（ ）
A．相离 B．外切 C．相交 D．内切
9．下列四组点，其中四个交点在同一个圆上的有（ ）
1菱形的四个点 2正方形的四个顶点 3平行四边形各边的中点 4矩形的各边中点
A．1 B．1和2 C．2和4 D．2
10．已知线段AB=2cm，和点A、点B距离都是2cm的点的集合是（ ）
A．线段AB的中垂线
B．分别以A、B为圆心，2cm为半径的⊙A 与⊙B的交点
C．分别以A、B为圆心，2cm为半径的⊙A 与⊙B
D．以AB中点为圆心，2cm为半径的圆
11.已知两圆半径满足方程
，圆心距为3．则两圆的位置关系是（ ）
A．内切 B．外切 C．相交 D．相离
12．如图，已知等边
边长
，下列以Ｏ为圆心的各圆中，半径是3cm的圆是（ ）
|
|
|
|
|
|
|
|
|
|
|
|
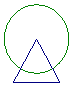
A B C D
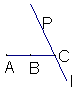
13．如下图，B是线段AC的中点，过点C的直线
与AC成
的角，在直线上取一点P，使
，则满足条件的点P的个数是（ ）
|
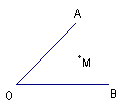14．如图，已知
和点M，求作一圆，使它过点O和M，且圆心在已知的边上，这样的圆能作几个？
第14题图
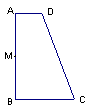15．如图，直角梯形ABCD中，AD∥BC，AB⊥BC，AD=4，BC=9，AB=12，M为AB的中点，以CD为直径画⊙P，判断点M与⊙P的位置关系．
第15题图
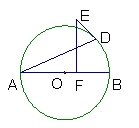16．如图，AB是⊙O的直径，AD是弦，E是⊙O外一点，作EF⊥AB于点F，交AD于点C，且ED=EC．
求证：DE是⊙O的切线．
第16题图
17．如图，⊙O的圆心是坐标原点，半径为2个单位，在坐标轴上找一点P，以P为圆心，1个单位长为半径作⊙P与⊙O相切．画出图形，并写出满足条件的所有点P的坐标．
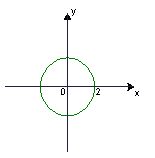
第17题图
第26课 正多边形和圆（含弧长和扇形面积）
1.扇形的圆心角为1500，扇形的面积为
cm2，则扇形的弧长为 ．
2.一个圆锥形零件底面圆半径
为4 cm，母线长为12 cm，则这个零件的展开图的圆心角
的度数是 ．
3.如图正△ABC的中心O恰好为扇形ODE的圆心，要使扇形ODE绕O无论怎样旋转，△ABC与扇形重叠部分的面积总等于△ABC的面积的
，则扇形的圆心角应为 ．
4.如图，A、B、C、D是圆周上的四个点，
，且弦AB＝8，CD＝4，则图中两个弓形（阴影）面积的和是 （结果保留三个有效数字）．
5.正六边形的两条平行边之间的距离为1，则它的边长为（ ）
A.
B.
C.
D.
6. 如图，AB为半圆O的直径，C为半圆上一点，且
为半圆的，设扇形AOC、△COB、弓形BC的面积分别为
、
、
，则下列结论正确的是（ ）
A.＜＜ B.＜＜ C.＜＜
D.＜＜
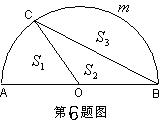
第7题图
7．在RT△ABC中，∠A=60°，∠B=90°，以A为圆心作圆与BC相切，圆A交AB于D，若BD=4厘米，则BC=（ ）厘米
A.4 B.8 C. 
D.2
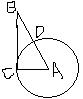
8. 如图，A是半径为1的⊙O外一点，OA＝2，AB切⊙O于B，弦BC∥OA，连结AC，则图中阴影部分的面积为（ ）
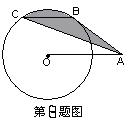
A.
B.
C.
D.
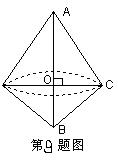
9. 如图，在△ABC中，∠BAC＝300，AC＝
，BC＝
，以直线AB为轴旋转一周得到一个几何体，则这个几何体的表面积是（ ）
A.
B.
C.
D.
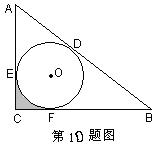10. 如图，⊙O内切于△ABC，切点分别为D、E、F，若∠C＝900，AD＝4，BD＝6，求图中阴影部分的面积．
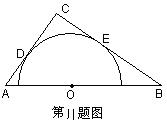11. 如图，在Rt△ABC中，∠C＝900，O点在AB上，半圆O切AC于D，切BC于E，AO＝15cm，BO＝20cm，求
的长．
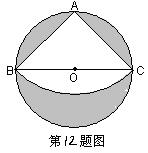
12. 如图，有一个直径是1米圆形铁皮，要从中剪出一个最大的圆心角为900的扇形ABC，求：
（1）被剪掉（阴影）部分的面积；
（2）用所留的扇形铁皮围成一个圆锥，该圆锥的底面半径是多少？
第27课 尺规作图
1．尺规作图是指 ．
2．某产品的标志图案如图（1）所示，要在所给的图形中，把A、B、C三个菱形通过一种或几种变换，使之变为与图（1）一样的图案
（1）请你在图（二）中作出变换后的图案（最终图案用实线表示）
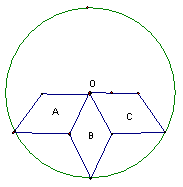
（2）你所用的变换方法是 （在以下变换方法中，选择一种正确的填到横线上，也可以用自己的话表述）
①将菱形B向上平移；
②将菱形B绕O旋转120
；
③将菱形B绕O旋转180．
（一） （二）
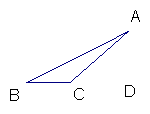3．已知
ABC与EFG是关于点D的中心对称图形，请将EFG补充完整．
4．如图，ABC是一块直角三角形余料，
工人师傅要把它加工成一个正方形零件，使C为正方形的一个顶点，其余三个顶点分别在AB、BC、AC边上．
(1) 试协助工人师傅用尺规画出裁割线（不写作法、保留作图痕迹）；
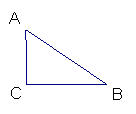(2)工人师傅测得AC＝80cm，BC=120cm，请帮助工人师傅算出按（1）题所画裁割线加工成的正方形的零件的边长．
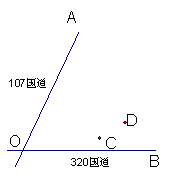5．如图，107国道OA和320国道OB在我市相交于O点，在的内部有工厂C和D,现要修建一个货站P，使P到OA、OB的距离相等，且使PC=PD,用尺规作出货站P的位置（不写作法，保留作图痕迹，写出结论）．
6．如图，已知ABC，(1)以直线l为对称轴，画出ABC关于直线l对称的
；
(2)将ABC向右平移，得到
，其中
是A的对称点，请画出（不写作法、保留作图痕迹）．
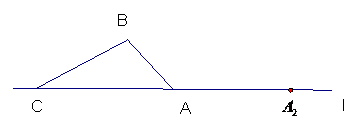
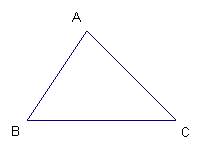
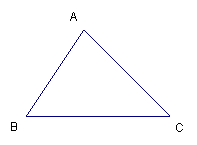7．某农场有一块三角形土地，准备分成面积相等的4块，分别承包给4位农户，请你设计两种不同的分配方案（在已给的图形中直接画图，不写作法保留作图痕迹）．
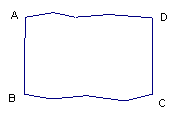8．现有一长方形木块的残留部分如图，其中AB、CD整齐且平行，BC、AD是参差不齐的毛边，请你在毛边附近有尺规画出一条与AB、CD都垂直的边（不写作法、保留作图痕迹）．
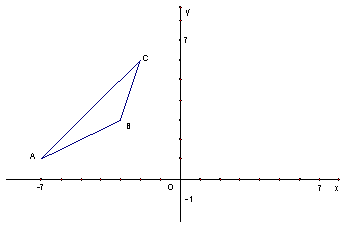
9．如图，已知ABC的三个顶点的坐标分别为A（－7，1）、B（－3，3）、C（－2，6）.
(1)求作一个三角形，使它与 ABC关于y轴对称．
(2)写出作出的三角形的三个顶点的坐标．
第28课 投影与视图
1．请写出三种视图都相同的两种几何体是 、 ．
2．同一形状的图形在同一灯光下可以得到 的图形．（填“同”或“不同”）
3．两个物体在同一灯光下的影子构成的两个三角形 相似三角形．（填“是”或“不是）
4．如图，一几何体的三视图如右：
那么这个几何体是 ．
5．两个物体的主视图都是圆，这两个物体可能是（ ）
A．圆柱体、圆锥体 B．圆柱体、正方体 C．圆柱体、球 D．圆锥体、球
6．在同一时刻，两根长度不等的竿子置于阳光之下，但它们的影长相等，那么这根竿子的相对位置是（ ）
A．两根都垂直于地面 B．两根平行斜插在地上
C．两根竿子不平行 D．一根倒在地上
7．两个不同长度的的物体在同一时刻同一地点的太阳光下得到的投影是（ ）
A．相等 B．长的较长 C．短的较长 D．不能确定
8．同一灯光下两个物体的影子可以是（ ）
A．同一方向 B．不同方向 C．相反方向 D．以上都是可能
9．棱长是1㎝的小立方体组成如图所示的几何体，那么这个几何体的表面积是（ ）
A．36
B．33 C．30 D．27
10．一个人离开灯光的过程中人的影长（ ）
A．不变 B．变短 C．变长 D．不确定
11.下列图中是太阳光下形成的影子是（ ）
 | |||||||
 | | | |||||
A
B
C
D
12．有一实物如图，那么它的主视图 （ ）
 |
A B C D
13．画出下图所示的三视图．
（第13题） （第14题）
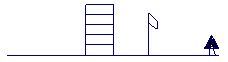
14．楼房,旗杆在路灯下的影子如图所示．试确定路灯灯炮的位置，再作出小树在路灯下的影子．（不写作法，保留作图痕迹）
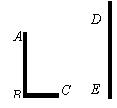
15．已知，如图,AB和DE是直立在地面上的两根立柱.AB=5m,某一时刻AB在太阳光下的投影BC=3m.（1）请你在图中画出此时DE在阳光下的投影；
（2）在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,计算DE的长.
 |
16．如图，一个棱长为10㎝的正方形，当你观察此物体时．
（1）在什么区域内只能看到一面？
（2）在什么区域内只能看到两个面？
（3）在什么区域内能看到三个面？
17．小强说：“同一时刻，阳光下影子越长的物体就越高”，你同意他的说法吗？小亮说：“同一时刻，灯光下影子越长的物体就越高”，你同意吗？说说你的理由．
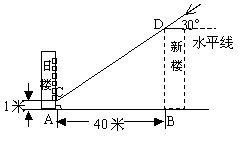
18．为解决楼房之间的挡光问题，某地区规定：两幢楼房间的距离至少为40米，中午12时不能挡光.如图，某旧楼的一楼窗台高1米，要在此楼正南方40米处再建一幢新楼.已知该地区冬天中午12时阳光从正南方照射，并且光线与水平线的夹角最小为30°，在不违反规定的情况下，请问新建楼房最高多少米？（结果精确到1米.
，
）
 |
第四单元 图形的认识检测卷（一）
（总分100分，时间60分钟）
一.选择题（本大题共12题，每题2分，共24分．每题的四个选项中，只有一个选项是符合要求的．）
1．□ABCD的对角线交于点O，下列结论错误的是（ ）
A. □ABCD是中心对称图形 B．△AOB≌△COD
C．△AOB≌△BOC D．△AOD与△BOC
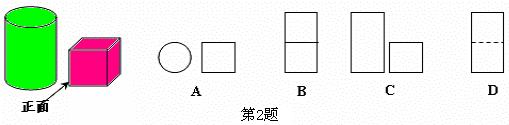2．如图，小明从正面观察一个圆柱体邮筒和一个正方体箱子，看到的是（ ）
3．在等边三角形、正五边形、正六边形、正七边形中，既是轴对称又是中心对称的图形是（ ）
A．等边三角形 B.正五边形 C.正六边形 D.正七边形
4．若等腰梯形两底之差等于一腰的长，那么这个梯形一内角是（ ）
A．
B．
C.
D.
5．花园内有一块边长为
的正方形土地，园艺师设计了四种不同图案，其中的阴影部分用于种植花草，种植花草面积最大的是（ ）
|
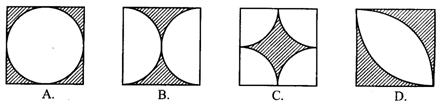
6．一位美术老师在课堂上进行立体模型素描教学时，把14个棱长为1分米的正方体摆在课桌上成如图形式，然后他把露出的表面都涂上不同的颜色，则被他涂上颜色部分的面积为（ ）
A． 33分米2 B．24分米2
C．21分米2 D．42分米2
7．如图
的度数是（ ）
A.550 B.1100 C.1250 D.1500
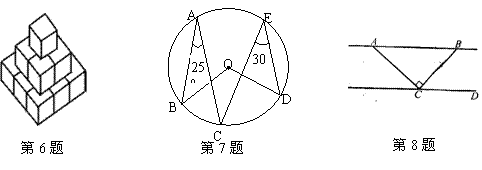
8．如图，AB∥CD，AC⊥BC，图中与∠CAB互余的角有（ ）
A．1个 B.2个 C.3个 D.4个
9．下列图形中，是轴对称而不是中心对称图形的是（ ）
Ａ．平行四边形 Ｂ．菱形 Ｃ．等腰梯形 Ｄ．直角梯形
10．冰淇淋蛋筒下部呈圆锥形，则蛋筒圆锥部分包装纸的面积（接缝忽略不计）是（ ）
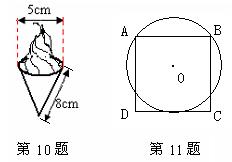A．20
B．40
C．20
D．40
11．如图，已知⊙O过正方形ABCD的顶点
A、B，且与CD边相切，若正方形的边
长为2，则圆的半径为（ ）
A．
B．
C．
D．1
12．已知：关于x的一元二次方程x2-(R＋r)x＋
d2＝0无实数根，其中R、r分别是⊙O1、⊙O2的半径，d为此两圆的圆心距，则⊙O1，⊙O2的位置关系为（ ）
A．外离 B．相切
C．相交 D．内含
二.填空题（本大题共8题，每题2分，共16分．把答案填在题中的横线上．）
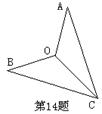13.如图，AD=BC，要使四边形ABCD是平行四边形，还需补充的一个条件是：
.
|
14．如图，这是小亮制作的风筝，为了平衡做成轴对称图形，已知 OC是对称轴，∠A=35°，∠ACO=30°，那么∠BOC= °．
15．已知圆锥的侧面展开图是一个半园，则这个圆锥的母线长与底面半径长的比是 ．
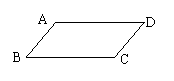
16．将边长为8cm的正方形ABCD的四边沿直线l想右滚动(不滑动)，当正方形滚动两周时正方形的顶点A所经过的路线的长是 cm．
|
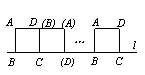
17．如图，⊙O的半径OA=6,以A为圆心，OA为半径的弧交⊙O于B、C，则BC= ．
18．如图，两建筑物AB和CD的水平距离为30米，从A点测得D点的俯角为30°，测得C点的俯角为60°，则建筑物CD的高为 米．
|
|
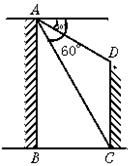
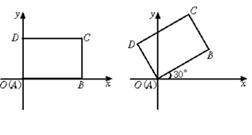
19．先将一矩形ABCD置于直角坐标系中，使点A与坐标系的原点重合，边AB、AD分别落在x轴、y轴上，再将此矩形在坐标平面内按逆时针方向绕原点旋转30°(如图19)，若AB＝4，BC＝3，则图中点B点的坐标为 点C的坐标 ．
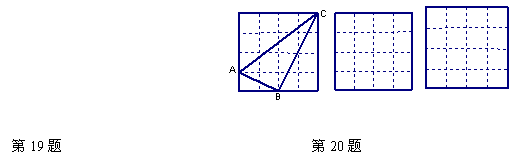
20．正方形网格中，小格的顶点叫做格点．小华按下列要求作图：①在正方形网格的三条不同的实线上各取一个格点，使其中任意两点不在同一条实线上；②连结三个格点，使之构成直角三角形．小华在左边的正方形网格中作出了Rt⊿ABC．请你按照同样的要求，在右边的两个正方形网格中各画出一个直角三角形，并使三个网格中的直角三角形互不全等．
三、解答题 (本大题共6题，共60分．解答应写出文字说明、证明过程或演算步骤．)
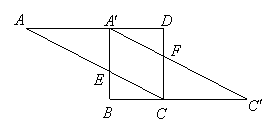
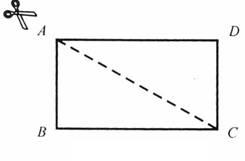
21．（本题满分10分）将图中的矩形
沿对角线
剪开，再把
沿着
方向平移，得到图中的
，除
与
全等外，你还可以指出哪几对全等的三角形（不能添加辅助线和字母）？请选择其中一对加以证明．
22．（本题满分10分）
如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作：
⑴ 请在网格中建立平面直角坐标系, 使A点坐标为(－2，4)，B点坐标为(－４，2)；
⑵ 在第二象限内的格点上画一点C, 使点C与线段AB组成一个以AB为底的等腰三角形, 且腰长是无理数, 则C点坐标是 ， △ABC的周长是 (结果保留根号)；
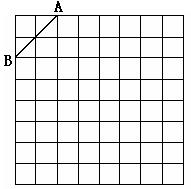⑶ 画出△ABC以点C为旋转中心、旋转180°后的△A′B′C, 连结AB′和A′B, 试说出四边形ABA′B′是何特殊四边形, 并说明理由.
23．（本题满分10分）
如图，四边形中，
，
，过的中点
作的垂线，交
的延长线于
．
求证：（1）四边形是菱形．
（2）
．
24．（本题满分10分）如图，O为圆柱形木块底面的圆心，过底面的一条弦AD，沿母线AB剖开，得剖面矩形ABCD，AD＝24 cm，AB＝25 cm．若
的长为底面周长的
，如图所示．
(1)求⊙O的半径；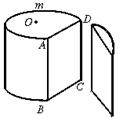 
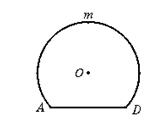
(2)求这个圆柱形木块的表面积．(结果可保留∏和根号)
25．（本题满分10分）
如图，平面直角坐标系中，四边形OABC为矩形，点A、B的坐标分别为（6，0），（6，8）．动点M、N分别从O、B同时出发，以每秒1个单位的速度运动．其中，点M沿OA向终点A运动，点N沿BC向终点C运动．过点N作NP⊥BC，交AC于P，连结MP．已知动点运动了x秒．
（1）P点的坐标为（ ， ）；（用含x的代数式表示）
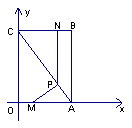（2）试求 ⊿MPA面积的最大值，并求此时x的值．
（3）请你探索：当x为何值时，⊿MPA是一个等腰三角形？
你发现了几种情况？写出你的研究成果．
26．（本题满分10分）如图，已知O为原点，点A的坐标为（4，3），
⊙A的半径为2．过A作直线平行于
轴，点P在直线上运动．
（１）当点P在⊙O上时，请你直接写出它的坐标；
（２）设点P的横坐标为12，试判断直线OP与⊙A的位置关系，并说明理由.
