中考试题分类汇编--函数综合题
1. 如图,已知点A(tanα,0),B(tanβ,0)在x轴正半轴上,点A在点B的左边,α、β 是以线段AB为 斜边、顶点C在x轴上方的Rt△ABC的两个锐角.
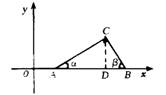
(1)若二次函数y=-x2-![]() kx+(2+2k-k2)的图象经过A、B两点,求它的解析式;
kx+(2+2k-k2)的图象经过A、B两点,求它的解析式;
(2)点C在(1)中求出的二次函数的图象上吗?请说明理由.
解:(1)∵ α,β是Rt△ABC的两个锐角,
∴ tanα·tanβ=1.tanα>0,tanβ>0.
由题知tanα,tanβ是方程
x2+![]() kx-(2+2k-k2)=0的两个根,
kx-(2+2k-k2)=0的两个根,
∴ tanx·tanβ=(2=2k-k2)=k2-2k-2,∴ k2-2k-2=1.
解得,k=3或k=-1.
而tanα+tanβ=-![]() k>0,
k>0,
∴ k<0.∴ k=3应舍去,k=-1.
故所求二次函数的解析式为y=-x2+![]() x-1.
x-1.
(2)不在.
过C作CD⊥AB于D.
令y=0,得-x2+![]() x-1=0,
x-1=0,
解得x1=![]() ,x2=2.
,x2=2.
∴ A(![]() ,0),B(2,0),AB=
,0),B(2,0),AB=![]() .
.
∴ tanα=![]() ,tanβ=2.设CD=m.则有CD=AD·tanα=
,tanβ=2.设CD=m.则有CD=AD·tanα=![]() AD.
AD.
∴ AD=2CD.
又CD=BD·tanβ=2BD,
∴ BD=![]() CD.
CD.
∴ 2m+![]() m=
m=![]() .
.
∴ m=![]() .∴ AD=
.∴ AD=![]() .
.
∴ C(![]() ,
,![]() ).
).
当x=![]() 时,y=
时,y=![]() ≠
≠![]()
∴ 点C不在(1)中求出的二次函数的图象上.
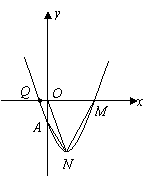 2.已知抛物线
2.已知抛物线![]() 经过点
经过点![]() .
.
(1)求抛物线的解析式.
(2)设抛物线顶点为![]() ,与
,与![]() 轴交点为
轴交点为![]() .求
.求![]() 的值.
的值.
(3)设抛物线与![]() 轴的另一个交点为
轴的另一个交点为![]() ,求四边形
,求四边形![]() 的面积.
的面积.
解:(1)解方程组![]()
得![]() ,
,![]() .
.
(2)顶点![]() .
.
(3)在![]() 中,令
中,令![]() 得
得![]() ,
,![]() ,
,
令![]() 得
得![]() 或
或![]() ,
,![]() .
.
![]() 四边形
四边形![]() (面积单位)
(面积单位)
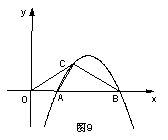 3.如图9,抛物线y=ax2+8ax+12a与
3.如图9,抛物线y=ax2+8ax+12a与![]() 轴交于A、B两点(点A在点B的左侧),抛物线上另有一点
轴交于A、B两点(点A在点B的左侧),抛物线上另有一点![]() 在第一象限,满足∠ ACB为直角,且恰使△OCA∽△OBC.
在第一象限,满足∠ ACB为直角,且恰使△OCA∽△OBC.
(1) 求线段OC的长.
(2) 求该抛物线的函数关系式.
(3) 在![]() 轴上是否存在点P,使△BCP为等腰三角形?
轴上是否存在点P,使△BCP为等腰三角形?
若存在,求出所有符合条件的P点的坐标;若不存在,
请说明理由.
解:(1)![]() ;(2)
;(2)![]() ;(3)4个点:
;(3)4个点:
![]()
4.已知函数y=![]() 和y=kx+l(k≠O).
和y=kx+l(k≠O).
(1)若这两个函数的图象都经过点(1,a),求a和k的值;
(2)当k取何值时,这两个函数的图象总有公共点?
解;(1)
∵两函数的图象都经过点(1,a),∴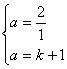 ∴
∴![]()
(2)将y=![]()
![]() 代人y=kx+l,消去y.得kx2+x一2=0.
代人y=kx+l,消去y.得kx2+x一2=0.
∵k≠O,∴要使得两函数的图象总有公共点,只要△≥0即可.
∵△=1+8k,
∴1+8k≥0,解得k≥一![]()
∴k≥一![]() 且k≠0.
且k≠0.
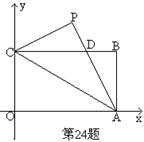 5.已知如图,矩形OABC的长OA=
5.已知如图,矩形OABC的长OA=![]() ,宽OC=1,将△AOC沿AC翻折得△APC。
,宽OC=1,将△AOC沿AC翻折得△APC。
(1)填空:∠PCB=____度,P点坐标为( , );
(2)若P,A两点在抛物线y=-![]() x2+bx+c上,求b,c的值,并说明点C在此抛物线上;
x2+bx+c上,求b,c的值,并说明点C在此抛物线上;
(3)在(2)中的抛物线CP段(不包括C,P点)上,是否存在一点M,使得四边形MCAP的面积最大?若存在,求出这个最大值及此时M点的坐标;若不存在,请说明理由.
(1)30,(![]() ,
,![]() );
);
(2)∵点P(![]() ,
,![]() ),A(
),A(![]() ,0)在抛物线上,故 -
,0)在抛物线上,故 -![]() ×
×![]() +b×
+b×![]() +c=
+c=![]() ,-
,-![]() ×3+b×
×3+b×![]() +c=0, ∴b=
+c=0, ∴b=![]() ,c=1. ∴抛物线的解析式为y=-
,c=1. ∴抛物线的解析式为y=-![]() x2+
x2+![]() x+1,C点坐标为(0,1). ∵-
x+1,C点坐标为(0,1). ∵-![]() ×02+
×02+![]() ×0+1=1,
×0+1=1,
∴ 点C在此抛物上.

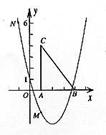 6.如图,二资助函数
6.如图,二资助函数![]() 的图象经过点M(1,—2)、N(—1,6).
的图象经过点M(1,—2)、N(—1,6).
(1)求二次函数![]() 的关系式.
的关系式.
(2)把Rt△ABC放在坐标系内,其中∠CAB = 90°,点A、B的坐标分别为(1,0)、(4,0),BC = 5。将△ABC沿x轴向右平移,当点C落在抛物线上时,求△ABC平移的距离.
解:(1)∵M(1,-2),N(-1,6)在二次函数y = x2+bx+c的图象上,
∴![]() 解得
解得![]()
二次函数的关系式为y = x2-4x+1.
(2)Rt△ABC中,AB = 3,BC = 5,∴AC = 4,
![]()
解得![]()
∵A(1,0),∴点C落在抛物线上时,△ABC向右平移![]() 个单位.
个单位.
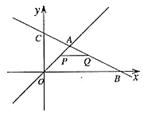
7.如图,在平面直角坐标系中,两个函数![]() 的图象交于点A。动点P从点O开始沿OA方向以每秒1个单位的速度运动,作PQ∥x轴交直线BC于点Q,以PQ为一边向下作正方形PQMN,设它与△OAB重叠部分的面积为S.
的图象交于点A。动点P从点O开始沿OA方向以每秒1个单位的速度运动,作PQ∥x轴交直线BC于点Q,以PQ为一边向下作正方形PQMN,设它与△OAB重叠部分的面积为S.
(1)求点A的坐标.
(2)试求出点P在线段OA上运动时,S与运动时间t(秒)的关系式.
(3)在(2)的条件下,S是否有最大值?若有,求出t为何值时,S有最大值,并求出最大值;若没有,请说明理由.
(4)若点P经过点A后继续按原方向、原速度运动,当正方形PQMN与△OAB重叠部分面积最大时,运动时间t满足的条件是____________.
 解:(1)由
解:(1)由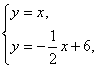 可得
可得![]()
∴A(4,4)。
(2)点P在y = x上,OP = t,
则点P坐标为![]()
点Q的纵坐标为![]() ,并且点Q在
,并且点Q在![]() 上。
上。
∴![]() ,
,
即点Q坐标为![]() 。
。
![]() 。
。
当![]() 时,
时,![]() 。
。
当![]() ,
,
![]()
当点P到达A点时,![]() ,
,
当![]() 时,
时,
![]()
![]() 。
。
(3)有最大值,最大值应在![]() 中,
中,
![]()
当![]() 时,S的最大值为12.
时,S的最大值为12.
(4)![]() .
.
8.已知一次函数y=![]() +m(O<m≤1)的图象为直线
+m(O<m≤1)的图象为直线![]() ,直线
,直线![]() 绕原点O旋转180°后得直线
绕原点O旋转180°后得直线![]() ,△ABC三个顶点的坐标分别为A(-
,△ABC三个顶点的坐标分别为A(-![]() ,-1)、B(
,-1)、B(![]() ,-1)、C(O,2).
,-1)、C(O,2).
(1)直线AC的解析式为________,直线![]() 的解析式为________ (可以含m);
的解析式为________ (可以含m);
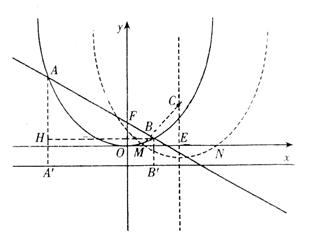
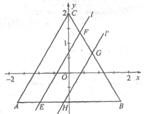
(2)如图,![]() 、
、![]() 分别与△ABC的两边交于E、F、G、H,当m在其范围内变化时,判断四边形EFGH中有哪些量不随m的变化而变化?并简要说明理由;
分别与△ABC的两边交于E、F、G、H,当m在其范围内变化时,判断四边形EFGH中有哪些量不随m的变化而变化?并简要说明理由;
(3)将(2)中四边形EFGH的面积记为S,试求m与S的关系式,并求S的变化范围;
(4)若m=1,当△ABC分别沿直线y=x与y=![]() x平移时,判断△ABC介于直线
x平移时,判断△ABC介于直线![]() ,
,![]() 之间部分的面积是否改变?若不变请指出来.若改变请写出面积变化的范围.(不必说明理由)
之间部分的面积是否改变?若不变请指出来.若改变请写出面积变化的范围.(不必说明理由)
解: (1)y=![]() +2 y=
+2 y=![]() -m
-m
(2)不变的量有:
①四边形四个内角度数不变, 理由略;
②梯形EFGH中位线长度不变(或EF+GH不变),理由略.
(3)S=![]() 0<m≤1 0<s≤
0<m≤1 0<s≤![]()
(4)沿y=![]() 平移时,面积不变;沿y=x平移时,面积改变,设其面积为
平移时,面积不变;沿y=x平移时,面积改变,设其面积为![]() ,则
,则
0<![]() ≤
≤![]()
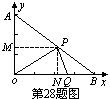
9. 如图,在平面直角坐标系中,点A、B分别在x轴、y轴上,线段OA、OB的长(0A<OB)是方程x2-18x+72=0的两个根,点C是线段AB的中点,点D在线段OC上,OD=2CD.
(1)求点C的坐标;
(2)求直线AD的解析式;
(3)P是直线AD上的点,在平面内是否存在点Q,使以0、A、P、Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
解:(1)OA=6,OB=12 ,
点C是线段AB的中点,OC=AC.
作CE⊥x轴于点E.
∴ OE=OA=3,CE=OB=6.
∴ 点C的坐标为(3,6).
(2)作DF⊥x轴于点F
△OFD∽△OEC,=,于是可求得OF=2,DF=4.
∴ 点D的坐标为(2,4).
设直线AD的解析式为y=kx+b.
把A(6,0),D(2,4)代人得![]() ,
,
解得![]() ,
,
∴ 直线AD的解析式为y=-x+6 .
(3)存在.
Q1(-3,3);
Q2(3,-3);
Q3(3,-3) ;
Q4(6,6) .
10. 在平面直角坐标系中,已知A(0,2),B(4,0),设P、Q分别是线段AB、OB上的动点,它们同时出发,点P以每秒3个单位的速度从点A向点B运动,点Q以每秒1个单位的速度从点B向点O运动.设运动时间为t(秒).
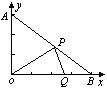 (1)用含t的代数式表示点P的坐标;
(1)用含t的代数式表示点P的坐标;
(2)当t为何值时,△OPQ为直角三角形?
(3)在什么条件下,以Rt△OPQ的三个顶点能确定一条对称轴平行于y轴的抛物线?选择一种情况,求出所确定的抛物线的解析式.
解:(1)作PM⊥y轴,PN⊥x轴.∵OA=3,OB=4,∴AB=5.
 ∵PM∥x轴,∴
∵PM∥x轴,∴![]() .∴
.∴![]() .∴PM=
.∴PM=![]() t.
t.
∵PN∥y轴,∴![]() .∴
.∴![]() .∴PN=3-
.∴PN=3-![]() t.
t.
∴点P的坐标为(![]() t,3-
t,3-![]() t).
t).
(2)①当∠POQ=90°时,t=0,△OPQ就是△OAB,为直角三角形.
②当∠OPQ=90°时,△OPN∽△PQN,∴PN2=ON•NQ.(3-![]() t)2=
t)2=![]() t(4-t-
t(4-t-![]() t).
t).
化简,得19t2-34t+15=0.解得t=1或t=![]() .
.
③当∠OQP=90°时,N、Q重合.∴4-t=![]() t,∴t=
t,∴t=![]() .
.
综上所述,当t=0,t=1,t=![]() ,t=
,t=![]() 时,△OPQ为直角三角形.
时,△OPQ为直角三角形.
(3)当t=1或t=![]() 时,即∠OPQ=90°时,以Rt△OPQ的三个顶点可以确定一条对称轴平行于y轴的抛物线.当t=1时,点P、Q、O三点的坐标分别为P(
时,即∠OPQ=90°时,以Rt△OPQ的三个顶点可以确定一条对称轴平行于y轴的抛物线.当t=1时,点P、Q、O三点的坐标分别为P(![]() ,
,![]() ),Q(3,0),O(0,0).设抛物线的解析式为y=a(x-3)(x-0),即y=a(x2-3x).将P(
),Q(3,0),O(0,0).设抛物线的解析式为y=a(x-3)(x-0),即y=a(x2-3x).将P(![]() ,
,![]() )代入上式,得a=-
)代入上式,得a=-![]() .∴y=-
.∴y=-![]() (x2-3x).
(x2-3x).
即y=-![]() x2+
x2+![]() x.
x.
说明:若选择t=![]() 时,点P、Q、O三点的坐标分别是P(
时,点P、Q、O三点的坐标分别是P(![]() ,
,![]() ),Q(
),Q(![]() ,0),O(0,0).求得抛物线的解析式为y=-
,0),O(0,0).求得抛物线的解析式为y=-![]() x2+
x2+![]() x,相应给分.
x,相应给分.
11.已知:抛物线![]() (m>0)与y轴交于点C,C点关于抛物线对称轴的对称点为C′点.
(m>0)与y轴交于点C,C点关于抛物线对称轴的对称点为C′点.
(1)求C点、C′点的坐标(可用含m的代数式表示)
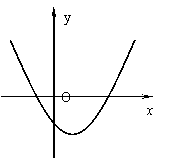 (2)如果点Q在抛物线的对称轴上,点P在抛物线上,以点C、C′、P、Q为顶点的四边形是平行四边形,求Q点和P点的坐标(可用含m的代数式表示)
(2)如果点Q在抛物线的对称轴上,点P在抛物线上,以点C、C′、P、Q为顶点的四边形是平行四边形,求Q点和P点的坐标(可用含m的代数式表示)
(3)在(2)的条件下,求出平行四边形的周长.
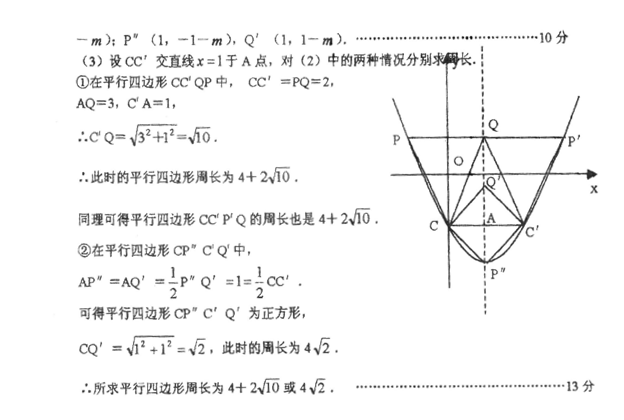

12.抛物线y=3(x-1)![]() +1的顶点坐标是( A )
+1的顶点坐标是( A )
A.(1,1) B.(-1,1) C.(-1,-1) D.(1,-1)
13.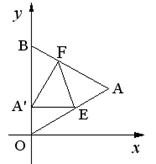 如图,△OAB是边长为
如图,△OAB是边长为![]() 的等边三角形,其中O是坐标原点,顶点B在
的等边三角形,其中O是坐标原点,顶点B在![]() 轴正方向上,将△OAB 折叠,使点A落在边OB上,记为A′,折痕为EF.
轴正方向上,将△OAB 折叠,使点A落在边OB上,记为A′,折痕为EF.
(1)当A′E//![]() 轴时,求点A′和E的坐标;
轴时,求点A′和E的坐标;
(2)当A′E//![]() 轴,且抛物线
轴,且抛物线![]() 经过点A′和E时,求抛物线与
经过点A′和E时,求抛物线与![]() 轴的交点的坐标;
轴的交点的坐标;
(3)当点A′在OB上运动,但不与点O、B重合时,能否使△A′EF成为直角三角形?若能,请求出此时点A′的坐标;若不能,请你说明理由.
解:(1)由已知可得∠A,OE=60o , A,E=AE
由A′E//![]() 轴,得△OA,E是直角三角形,
轴,得△OA,E是直角三角形,
设A,的坐标为(0,b)
AE=A,E=![]() ,OE=2b
,OE=2b
![]()
所以b=1,A,、E的坐标分别是(0,1)与(![]() ,1)
,1)
(2)因为A,、E在抛物线上,所以
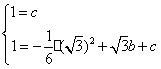
所以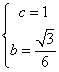 ,函数关系式为
,函数关系式为![]()
由![]() 得
得![]()
与x轴的两个交点坐标分别是(![]() ,0)与(
,0)与(![]() ,0)
,0)
(3)不可能使△A′EF成为直角三角形.
∵∠FA,E=∠FAE=60o,若△A′EF成为直角三角形,只能是∠A,EF=90o或∠A,FE=90o
若∠A,EF=90o,利用对称性,则∠AEF=90o, A,、E、A三点共线,O与A重合,与已知矛盾;
同理若∠A,FE=90o也不可能
所以不能使△A′EF成为直角三角形.
14.已知抛物线y=x²—4x+1.将此抛物线沿x轴方向向左平移4个单位长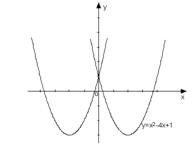 度,得到一条新的抛物线.
度,得到一条新的抛物线.
⑴求平移后的抛物线解析式;
⑵若直线y=m与这两条抛物线有且只有四个交点,求实数m的取值范围;
⑶若将已知的抛物线解析式改为y=ax²+bx+c(a>0,b<0),并将此抛物线沿x轴方向向左平移 -![]() 个单位长度,试探索问题⑵.
个单位长度,试探索问题⑵.
(1)解:![]()
配方,得![]() ,
,
向左平移4个单位,得![]()
∴平移后得抛物线的解析式为![]()
(2)由(1)知,两抛物线的顶点坐标为(2,3),(-2,-3)
解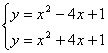 ,得
,得![]()
∴两抛物线的交点为(0,1)
由图象知,若直线y=m与两条抛物线有且只有四个交点时,
m>-3且m≠1
(3)由![]() 配方得,
配方得,![]()
向左平移![]() 个单位长度得到抛物线的解析式为
个单位长度得到抛物线的解析式为
![]()
∴两抛物线的顶点坐标分别为![]() ,
,![]()
解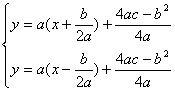 得,
得,![]()
∴两抛物线的交点为(0,c)
由图象知满足(2)中条件的m的取值范围是:
m>![]() 且m≠c
且m≠c
15.直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于B、A两点.
轴交于B、A两点.
⑴求B、A两点的坐标;
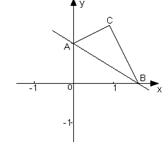 ⑵把△AOB以直线AB为轴翻折,点O落在平
⑵把△AOB以直线AB为轴翻折,点O落在平
面上的点C处,以BC为一边作等边△BCD
求D点的坐标.
解:如图(1)令x=0,由![]() 得 y=1
得 y=1
令y=0,由![]() 得
得![]()
∴B点的坐标为(![]() ,0),A点的坐标为(0,1)
,0),A点的坐标为(0,1)
(2)由(1)知OB=![]() ,OA=1
,OA=1
∴tan∠OBA=![]() =
=![]() ∴∠OBA=30°
∴∠OBA=30°
∵△ABC和△ABO关于AB成轴对称
∴BC=BO=![]() ,∠CBA=∠OBA=30° ∴ ∠CBO=60°
,∠CBA=∠OBA=30° ∴ ∠CBO=60°
过点C作CM⊥x轴于M,则在Rt△BCM中
CM=BC×sin∠CBO=![]() ×sin60°=
×sin60°=![]()
BM=BC×cos∠CBO=![]() ×cos60°=
×cos60°=![]() ∴OM=OB-BM=
∴OM=OB-BM=![]() -
-![]() =
=![]()
∴C点坐标为(![]() ,
,![]() )
)
连结OC
∵OB=CB,∠CBO=60°
∴△BOC为等边三角形
过点C作CE∥x轴,并截取CE=BC则∠BCE=60°
 连结BE则△BCE为等边三角形.
连结BE则△BCE为等边三角形.
作EF⊥x轴于F,则EF= CM=![]() ,BF=BM=
,BF=BM=![]()
OF=OB+BF=![]() +
+![]() =
=![]()
∴点E坐标为(![]() ,
,![]() )
)
∴D点的坐标为(0,0)或(![]() ,
,![]() )
)
16.已知抛物线y=ax2+bx+c经过A,B,C三点,当x≥0时,其图象如图所示.
(1)求抛物线的解析式,写出抛物线的顶点坐标;
(2)画出抛物线y=ax2+bx+c当x<0时的图象;
(3)利用抛物线y=ax2+bx+c,写出x为何值时,y>0.
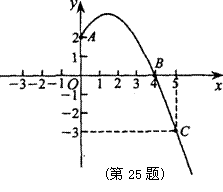 |
解:(1)由图象,可知A(0,2),B(4,0),C(5,-3),
得方程组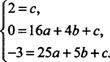 解得
解得![]()
∴抛物线的解析式为![]()
顶点坐标为![]()
(2)所画图如图.
(3)由图象可知,当-1<x<4时,y>0.
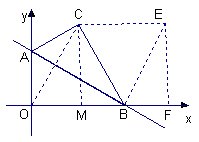
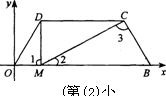
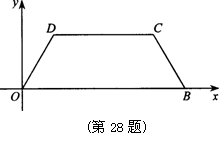 17.如图,在平面直角坐标系中,O为坐标原点,B(5,0),M为等腰梯形OBCD底边OB上一点,OD=BC=2,∠DMC=∠DOB=60°.
17.如图,在平面直角坐标系中,O为坐标原点,B(5,0),M为等腰梯形OBCD底边OB上一点,OD=BC=2,∠DMC=∠DOB=60°.
(1)求直线CB的解析式:
(2)求点M的坐标;
(3)∠DMC绕点M顺时针旋转α(30°<α<60°)后,得到∠D1MC1(点D1,C1依次与点D,C对应),射线MD1交直线DC于点E,射线MC1交直线CB于点F,设DE=m,BF=n.
求m与n的函数关系式.
解:(1)过点C作CA⊥OB,垂足为A.在Rt△ABC中,∠CAB=90°,∠CBO=60°,
0D=BC=2,∴CA=BC·sin∠CBO=![]() , BA=BC·cos∠CBO=1.
, BA=BC·cos∠CBO=1.
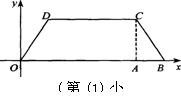 ∴点C的坐标为(4,
∴点C的坐标为(4,![]() ).
).
设直线CB的解析式为y=kx+b,由B(5,0),C(4,![]() ),
),
得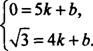 解得
解得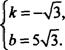
∴直线CB的解析式为y=-![]() x+5
x+5![]() .
.
(2)∵∠CBM+∠2+∠3=180°,∠DMC+∠1+∠2=180°,∠CBM=∠DMC=∠DOB=60°
∴∠2+∠3=∠1+∠2,∴∠1=∠3.
 ∴△ODM∽△BMC.
∴△ODM∽△BMC.
![]()
∴OD·BC=BM·OM.
∵B点为(5,0),∴OB=5.
设OM=x,则BM=5-x.
∵OD=BC=2,∴2×2=x(5-x).
 解得x1=1,x2=4.
解得x1=1,x2=4.
∴M点坐标为(1,0)或(4,0).
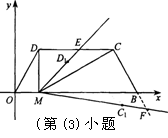
(3)(I)当M点坐标为(1,0)时,
如图①,OM=1,BM=4.
∵DC∥OB,∴∠MDE=∠DMO.
又∠DMO=∠MCB,∴∠MDE=∠MCB.
∵∠DME=∠CMF=a,∴△DME∽△CMF.
![]()
∴CF=2DE.
∵CF=2+n,DE=m,
∴2+n=2m,即m=1+![]() (0<n<4).
(0<n<4).
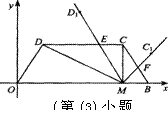
(Ⅱ)当M点坐标为(4,0)时,如图②.
OM=4,BM=1.
同理可得△DME∽△CMF,
![]()
∴DE=2CF.
∵CF=2-n,DE=m,∴m=2(2-n),即m=4-2n(![]() <n<1).
<n<1).
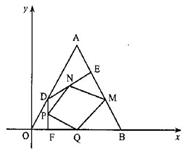 18.如图,边长为1的等边三角形OAB的顶点O为坐标原点,点B在x轴的正半轴上,点A在第一象限,动点D在线段OA上移动(不与O,A重合),过点D作DE⊥AB,垂足为E,过点D作DF⊥OB,垂足为F。点M,N,P,Q分别是线段BE,ED,DF,FB的中点。连接MN,NP,PQ,QM。记OD的长为t .
18.如图,边长为1的等边三角形OAB的顶点O为坐标原点,点B在x轴的正半轴上,点A在第一象限,动点D在线段OA上移动(不与O,A重合),过点D作DE⊥AB,垂足为E,过点D作DF⊥OB,垂足为F。点M,N,P,Q分别是线段BE,ED,DF,FB的中点。连接MN,NP,PQ,QM。记OD的长为t .
(1) 当![]() 时,分别求出点D和点E的坐标;
时,分别求出点D和点E的坐标;
(2) 当![]() 时,求直线DE的函数表达式;
时,求直线DE的函数表达式;
(3)如果记四边形MNPQ的面积为S,那么请写出面积S与变量t之间的函数关系式,并写出自变量t的取值范围,是否存在s的最大值?若存在,求出这个最大值及此时t的值;若不存在,请说明理由。

19.如图,在![]() 中,
中,![]() ,点
,点![]() ,
,![]() 在直线
在直线![]() 上运动,设
上运动,设![]() ,
,![]() .
.
(1)如果![]() ,
,![]() ,试确定
,试确定![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
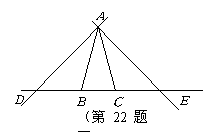 (2)如果
(2)如果![]() 的度数为
的度数为![]() ,
,![]() 的度数为
的度数为![]() ,当
,当![]() 满足怎样的关系式时,(1)中
满足怎样的关系式时,(1)中![]() 与
与![]() 之间的函数关系式还成立,试说明理由.
之间的函数关系式还成立,试说明理由.
解:(1)在![]() 中,
中,![]() ,
,
![]() ,
,
![]() .
.
又![]() ,
,
![]() .
.
又![]() ,
,
![]() .
.
![]() .
.
![]() .
.
即![]() ,所以
,所以![]() .
.
(2)当![]() 满足关系式
满足关系式![]() 时,函数关系式
时,函数关系式![]() 仍然成立.
仍然成立.
此时,![]() .
.
又![]() ,
,
![]() .
.
又![]() 仍然成立.
仍然成立.
从而(1)中函数关系式![]() 成立.
成立.
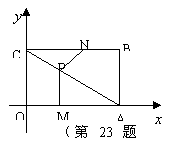 20.如图,平面直角坐标系中,四边形
20.如图,平面直角坐标系中,四边形![]() 为矩形,点
为矩形,点![]() 的坐标分别为
的坐标分别为![]() ,动点
,动点![]() 分别从
分别从![]() 同时出发,以每秒1个单位的速度运动.其中,点
同时出发,以每秒1个单位的速度运动.其中,点![]() 沿
沿![]() 向终点
向终点![]() 运动,点
运动,点![]() 沿
沿![]() 向终点
向终点![]() 运动,过点
运动,过点![]() 作
作![]() ,交
,交![]() 于
于![]() ,连结
,连结![]() ,已知动点运动了
,已知动点运动了![]() 秒.
秒.
(1)![]() 点的坐标为( , )(用含
点的坐标为( , )(用含![]() 的代数式表示);
的代数式表示);
(2)试求![]() 面积
面积![]() 的表达式,并求出面积
的表达式,并求出面积![]() 的最大值及相应的
的最大值及相应的![]() 值;
值;
(3)当![]() 为何值时,
为何值时,![]() 是一个等腰三角形?简要说明理由.
是一个等腰三角形?简要说明理由.
解:(1)由题意可知,![]() ,
,![]() ,
,
![]() 点坐标为
点坐标为![]() .
.
(2)设![]() 的面积为
的面积为![]() ,在
,在![]() 中,
中,![]() ,
,![]() 边上的高为
边上的高为![]() ,其中
,其中![]() .
.
![]() .
.
![]() 的最大值为
的最大值为![]() ,此时
,此时![]() .
.
(3)延长![]() 交
交![]() 于
于![]() ,则有
,则有![]() .
.
 ①若
①若![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
②若![]() ,则
,则![]() ,
,
![]() .
.
③若![]() ,则
,则![]() .
.
![]() ,
,
![]() 在
在![]() 中,
中,![]() .
.
![]() ,
,![]() .
.
综上所述,![]() ,或
,或![]() ,或
,或![]() .
.
21. (2006·北京市海淀区)已知抛物线![]() 的部分图象如图1所示。
的部分图象如图1所示。
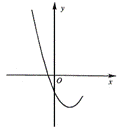
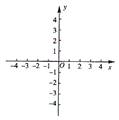
图1 图2
(1)求c的取值范围;
(2)若抛物线经过点(0,-1),试确定抛物线![]() 的解析式;
的解析式;
(3)若反比例函数![]() 的图象经过(2)中抛物线上点(1,a),试在图2所示直角坐标系中,画出该反比例函数及(2)中抛物线的图象,并利用图象比较
的图象经过(2)中抛物线上点(1,a),试在图2所示直角坐标系中,画出该反比例函数及(2)中抛物线的图象,并利用图象比较![]() 与
与![]() 的大小.22. 解:(1)根据图象可知
的大小.22. 解:(1)根据图象可知![]()
且抛物线![]() 与x轴有两个交点
与x轴有两个交点
所以一元二次方程![]() 有两个不等的实数根。
有两个不等的实数根。
所以![]() ,且
,且![]()
所以![]()
(2)因为抛物线经过点(0,-1)
把![]() 代入
代入![]()
得![]()
故所求抛物线的解析式为![]()
(3)因为反比例函数![]() 的图象经过抛物线
的图象经过抛物线![]() 上的点(1,a)
上的点(1,a)
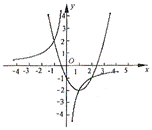 把
把![]() 代入
代入![]() ,得
,得![]()
把![]() 代入
代入![]() ,得
,得![]()
所以![]()
画出![]() 的图象如图所示.
的图象如图所示.
观察图象,![]() 除交点(1,-2)外,还有两个交点大致为
除交点(1,-2)外,还有两个交点大致为![]() 和
和![]()
把![]() 和
和![]() 分别代入
分别代入![]() 和
和![]() 可知,
可知,
![]() 和
和![]() 是
是![]() 的两个交点
的两个交点
根据图象可知:当![]() 或
或![]() 或
或![]() 时,
时,![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]()
22.已知抛物线y=ax2+bx+c经过点(1,2).
(1)若a=1,抛物线顶点为A,它与x轴交于两点B、C,且△ABC为等边三角形,求b的值.
(2)若abc=4,且a≥b≥c,求a+b+c的最小值.
解:⑴由题意,a+b+c=2, ∵a=1,∴b+c=1
抛物线顶点为A(-,c-)
设B(x1,0),C(x2,0),∵x1+x2=-b,x1x2=c,△=b2-4c>0
∴BC= x1-x2===
∵△ABC为等边三角形,∴ -c=
即b2-4c=2·,∵b2-4c>0,∴=2
∵c=1-b, ∴b2+4b-16=0, b=-2±2
所求b值为-2±2
⑵∵a≥b≥c,若a<0,则b<0,c<0,a+b+c<0,与a+b+c=2矛盾.
∴a>0.
∵b+c=2-a,bc=
∴b、c是一元二次方程x2-(2-a)x+=0的两实根.
∴△=(2-a)2-4×≥0,
∴a3-4a2+4a-16≥0, 即(a2+4)(a-4)≥0,故a≥4.
∵abc>0,∴a、b、c为全大于0或一正二负.
①若a、b、c均大于0,∵a≥4,与a+b+c=2矛盾;
②若a、b、c为一正二负,则a>0,b<0,c<0,
则a+b+c=a-b-c=a-(2-a)=2a-2,
∵ a≥4,故2a-2≥6
当a=4,b=c=-1时,满足题设条件且使不等式等号成立.
故a+b+c的最小值为6.
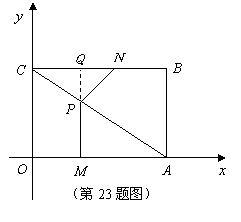
 23. 已知抛物线
23. 已知抛物线![]() 与y
与y
轴的交点为C,顶点为M,直线CM的解析式 y=-x+2
并且线段CM的长为![]()
(1) 求抛物线的解析式。
(2) 设抛物线与x轴有两个交点A(X1 ,0)、B(X2 ,0),
且点A在B的左侧,求线段AB的长。
(3) 若以AB为直径作⊙N,请你判断直线CM与⊙N的位置关系,并说明理由。
(1)解法一:由已知,直线CM:y=-x+2与y轴交于点C(0,2)抛物线![]() 过点C(0,2),所以c=2,抛物线
过点C(0,2),所以c=2,抛物线![]() 的顶点M
的顶点M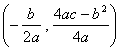 在直线CM上,所以
在直线CM上,所以![]()
若b=0,点C、M重合,不合题意,舍去,所以b=-2。即M![]()
过M点作y轴的垂线,垂足为Q,在![]()
所以,![]() ,解得,
,解得,![]() 。
。
∴所求抛物线为:![]() 或
或![]() 以下同下。
以下同下。
(1)解法二:由题意得C(0 , 2),设点M的坐标为M(x ,y)
∵点M在直线![]() 上,∴
上,∴![]()
由勾股定理得![]() ,∵
,∵![]()
![]()
∴![]() =
=![]() ,即
,即![]()
解方程组 ![]() 得
得![]()
![]()
∴M(-2,4) 或 M‘ (2,0)
当M(-2,4)时,设抛物线解析式为![]() ,∵抛物线过(0,2)点,
,∵抛物线过(0,2)点,
∴![]() ,∴
,∴![]()
当M‘(2,0)时,设抛物线解析式为![]()
∵抛物线过(0,2)点,∴![]() ,∴
,∴![]()
 ∴所求抛物线为:
∴所求抛物线为:![]() 或
或![]()
(2)∵抛物线与x轴有两个交点,
∴![]() 不合题意,舍去。
不合题意,舍去。
∴抛物线应为:![]()
抛物线与x轴有两个交点且点A在B的左侧,∴![]() ,得
,得
![]()
(3)∵AB是⊙N的直径,∴r =![]() , N(-2,0),又∵M(-2,4),∴MN = 4
, N(-2,0),又∵M(-2,4),∴MN = 4
设直线![]() 与x轴交于点D,则D(2,0),∴DN = 4,可得MN = DN,∴
与x轴交于点D,则D(2,0),∴DN = 4,可得MN = DN,∴
![]() ,作NG⊥CM于G,在
,作NG⊥CM于G,在![]()
![]() = r
= r
即圆心到直线CM的距离等于⊙N的半径,∴直线CM与⊙N相切
24. 已知:抛物线y=-x2+4x-3与x轴相交于A、B两点(A点在B点的左侧),顶点为P.
(1)求A、B、P三点坐标;
(2) 在下面的直角坐标系内画出此抛物线的简图,并根据简图写出当x取何值时,函数值y大于零;
(3)确定此抛物线与直线y=-2x+6公共点的个数,并说明理由.
解:(1)求得A(1,0),B (3,0), P (2,1)
(2)作图正确 当1<x<3时,y>0
 (3)由题意列方程组得:
(3)由题意列方程组得:![]()
转化得:x2-6x+9=0
△ =0,∴方程的两根相等,
方程组只有一组解
∴此抛物线与直线有唯一的公共点
25. 已知:如图,A(0,1)是y轴上一定点,B是x轴上一动点,以AB为边,在∠OAB的外部作∠BAE=∠OAB ,过B作BC⊥AB,交AE于点C.
(1)当B点的横坐标为时,求线段AC的长;
 (2)当点B在x轴上运动时,设点C的纵、横坐标分别为y、x,试求y与x的函数关系式(当点B运动到O点时,点C也与O点重合);
(2)当点B在x轴上运动时,设点C的纵、横坐标分别为y、x,试求y与x的函数关系式(当点B运动到O点时,点C也与O点重合);
(3)设过点P(0,-1)的直线l与(2)中所求函数的图象有两个公共点M1(x1,y1)、M2(x2,y2),且x12+x22-6(x1+x2)=8,求直线l的解析式.
解:(1)方法一:在Rt△AOB中,可求得AB=![]()
 ∵∠OAB=∠BAC,∠AOB=∠ABC=Rt∠ ,∴△ABO∽△ABC ,∴
∵∠OAB=∠BAC,∠AOB=∠ABC=Rt∠ ,∴△ABO∽△ABC ,∴![]() ,由此可求得:AC=
,由此可求得:AC=![]()
方法二:由题意知:tan∠OAB=
![]()
![]()
(2)方法一:当B不与O重合时,延长CB交y轴于点D,过C作CH⊥x轴,交x轴于点H,则可证得AC=AD,BD=--4′
∵AO⊥OB,AB⊥BD,∴△ABO∽△BDO,则OB2=AO×OD----6′,即![]()
化简得:y=![]() ,当O、B、C三点重合时,y=x=0,∴y与x的函数关系式为:y=
,当O、B、C三点重合时,y=x=0,∴y与x的函数关系式为:y=![]()
方法二:过点C作CG⊥x轴,交AB的延长线于点H,则AC2=(1-y)2+x2=(1+y)2,化简即可得。
(3)设直线的解析式为y=kx+b,则由题意可得: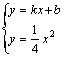 ,消去y得:x2-4kx-4b=0,则有
,消去y得:x2-4kx-4b=0,则有![]() ,由题设知:
,由题设知:
x12+x22-6(x1+x2)=8,即(4k)2+8b-24k=8,且b=-1,则16k2-24k -16=0,解之得:k1=2,k2=![]() ,当k1=2、b=-1时,
,当k1=2、b=-1时,
△=16k2+16b=64-16>0,符合题意;当k2=![]() ,b=-1时,△=16k2+16b=4-16<0,不合题意(舍去),∴所求的直线l的解析式为:y=2x-1
,b=-1时,△=16k2+16b=4-16<0,不合题意(舍去),∴所求的直线l的解析式为:y=2x-1
26.如图,已知抛物线与x轴交于A(m,0)、B(n,0)两点,与y轴交于点C(0, 3),点P是抛物线的顶点,若m-n= -2,m·n =3.
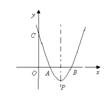 (1)求抛物线的表达式及P点的坐标;
(1)求抛物线的表达式及P点的坐标;
(2)求△ACP的面积S△ACP.
解: (1)设抛物线的表达式为y=ax2+bx+c,∵抛物线过C(0,3),∴c=3,
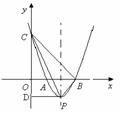 又∵抛物线与x轴交于A(m,0)、B(n,0)两点,
又∵抛物线与x轴交于A(m,0)、B(n,0)两点,
∴m、n为一元二次方程ax2+bx+3=0的解,
∴m+n=-![]() ,mn=
,mn=![]() ,
,
由已知m-n= -2,m·n =3,∴解之得a=1,b=-4;m=1,n=3,
∴ 抛物线的表达式为y=x2-4x+3,P点的坐标是(2,1)
(2)由(1)知,抛物线的顶点P(2,-1),过P作PD垂直于y轴于点D,所以,S△BCP =S梯形CBPD-S△CPD=S△COB+ S梯形OBPD- S△CPD,
∵B(3,0),C(0,3),
∴S△BCP
=S△COB+ S梯形OBPD- S△CPD=![]() ×3×3+
×3×3+![]() ×1×(3+2)-
×1×(3+2)-![]() ×2×4=3.
×2×4=3.
27.已知抛物线![]() :
:![]() (
(![]() ,
,![]() 为常数,且
为常数,且![]() ,
,![]() )的顶点为
)的顶点为![]() ,与
,与![]() 轴交于点
轴交于点![]() ;抛物线
;抛物线![]() 与抛物线
与抛物线![]() 关于
关于![]() 轴对称,其顶点为
轴对称,其顶点为![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
注:抛物线![]() 的顶点坐标为
的顶点坐标为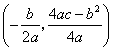 .
.
(1)请在横线上直接写出抛物线![]() 的解析式:________________________;
的解析式:________________________;
(2)当![]() 时,判定
时,判定![]() 的形状,并说明理由;
的形状,并说明理由;
(3)抛物线![]() 上是否存在点
上是否存在点![]() ,使得四边形
,使得四边形![]() 为菱形?如果存在,请求出
为菱形?如果存在,请求出![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
解:(1)![]() .
.
(2)当![]() 时,
时,![]() 为等腰直角三角形.
为等腰直角三角形.
理由如下:
如图:![]() 点
点![]() 与点
与点![]() 关于
关于![]() 轴对称,点
轴对称,点![]() 又在
又在![]() 轴上,
轴上,
![]() .
.
过点![]() 作抛物线
作抛物线![]() 的对称轴交
的对称轴交![]() 轴于
轴于![]() ,过点
,过点![]() 作
作![]() 于
于![]() .
.
![]() 当
当![]() 时,顶点
时,顶点![]() 的坐标为
的坐标为![]() ,
,![]() .
.
又![]() 点
点![]() 的坐标为
的坐标为![]() ,
,
![]() .
.![]() .
.
从而![]() ,
,![]() .
.
由对称性知![]() ,
,![]() .
.
![]() 为等腰直角三角形.
为等腰直角三角形.
(3)假设抛物线![]() 上存在点
上存在点![]() ,使得四边形
,使得四边形![]() 为菱形,则
为菱形,则![]() .
.
由(2)知,![]() ,
,![]() .
.
从而![]() 为等边三角形.
为等边三角形.
![]() .
.
![]() 四边形
四边形![]() 为菱形,且点
为菱形,且点![]() 在
在![]() 上,
上,![]() 点
点![]() 与点
与点![]() 关于
关于![]() 对称.
对称.
![]() 与
与![]() 的交点也为点
的交点也为点![]() ,因此
,因此![]() .
.
![]() 点
点![]() 的坐标分别为
的坐标分别为![]() ,
,
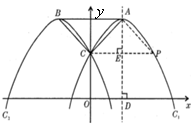
![]() .
.
在![]() 中,
中,![]() .
.
![]() ,
,![]() .
.
故抛物线![]() 上存在点
上存在点![]() ,使得四边形
,使得四边形![]() 为菱形,此时
为菱形,此时![]() .
.
 28.如图10(单位:m),等腰三角形ABC以2米/秒的速度沿直线L向正方形移动,直到AB与CD重合。设x秒时,三角形与正方形重叠部分的面积为y
28.如图10(单位:m),等腰三角形ABC以2米/秒的速度沿直线L向正方形移动,直到AB与CD重合。设x秒时,三角形与正方形重叠部分的面积为y![]() .
.
(1)写出y与x的关系式;
(2)当x=2,3.5时,y分别是多少?
(3)当重叠部分的面积是正方形面积的一半时,
三角形移动了多长时间?
(1)y=2x2
(2)8;24.5
(3)5秒
29、 如图,已知抛物线L1: y=x2-4的图像与x有交于A、C两点,
(1)若抛物线l2与l1关于x轴对称,求l2的解析式;
(2)若点B是抛物线l1上的一动点(B不与A、C重合),以AC为对角线,A、B、C三点为顶点的平行四边形的第四个顶点定为D,求证:点D在l2上;
(3)探索:当点B分别位于l1在x轴上、下两部分的图像上时,平行四边形ABCD的面积是否存在最大值和最小值?若存在,判断它是何种特殊平行四边形,并求出它的面积;若不存在,请说明理由.
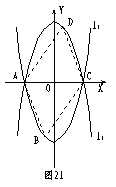
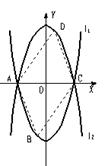
解:设l2的解析式为y=a(x-h)2+k
∵l2与x轴的交点A(-2,0),C(2,0),顶点坐标是(0,-4),l1与l2关于x轴对称,
∴l2过A(-2,0),C(2,0),顶点坐标是(0,4)
∴y=ax2+4
∴0=4a+4 得 a=-1
∴l2的解析式为y=-x2+4
(2)设B(x1 ,y1)
∵点B在l1上
∴B(x1 ,x12-4)
∵四边形ABCD是平行四边形,A、C关于O对称
∴B、D关于O对称
∴D(-x1 ,-x12+4).
将D(-x1 ,-x12+4)的坐标代入l2:y=-x2+4
∴左边=右边
∴点D在l2上.
(3)设平行四边形ABCD的面积为S,则
S=2*S△ABC =AC*y1=4y1
a.当点B在x轴上方时,y1>0
∴S=4y1 ,它是关于y1的正比例函数且S随y1的增大而增大,
∴S既无最大值也无最小值
b.当点B在x轴下方时,-4≤y1<0
∴S=-4y1 ,它是关于y1的正比例函数且S随y1的增大而减小,
∴当y1 =-4时,S由最大值16,但他没有最小值
此时B(0,-4)在y轴上,它的对称点D也在y轴上.9分
∴AC⊥BD
∴平行四边形ABCD是菱形
此时S最大=16.
30.已知关于x的二次函数![]() 与
与![]() ,这两个二次函数的图象中的一条与x轴交于A, B两个不同的点.
,这两个二次函数的图象中的一条与x轴交于A, B两个不同的点.
(l)试判断哪个二次函数的图象经过A, B两点;
(2)若A点坐标为(-1, 0),试求B点坐标;
(3)在(2)的条件下,对于经过A, B两点的二次函数,当x取何值时,y的值随x值的增大而减小?
解:(l)对于关于x的二次函数y =![]()
由于△=(-m )
2-4×l×![]() =-m2-2<0,
=-m2-2<0,
所以此函数的图象与x轴没有交点
对于关于x的二次函数 y =![]() .
.
由于△=(-m ) 2-4
×l×![]() =-m2-2<0,
=-m2-2<0,
所以此函数的图象与x轴没有交点
对于关于x的二次函数![]()
由于![]()
所以此函数的图象与x轴有两个不同的交点.
故图象经过A、B两点的二次函数为![]()
(2 )将A(-1,0)代入![]() ,得
,得![]() =0.
=0.
整理,得m2-2m = 0 .
解之,得m=0,或m = 2.
当m =0时,y=x2-1.令y = 0,得x2-1 = 0.
解这个方程,得x1=-1,x2=1
此时,B点的坐标是B (l, 0).
当m=2时,y=x2-2x-3.令y=0,得x2-2x-3=0.
解这个方程,得x1=-1,x2=3
此时,B点的坐标是B(3,0).
(3) 当m =0时,二次函数为y=x2-1,此函数的图象开口向上,对称轴为x=0,所以当x<0时,函数值 y 随:的增大而减小.
当m=2时,二次函数为y = x2-2 x-3 = (x-1)2-4, 此函数的图象开口向上,对称轴为x = l,所以当x < l 时,函数值y随x的增大而减小.
31.如图1,已知直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点.
两点.
(1)求![]() 两点的坐标;
两点的坐标;
(2)求线段![]() 的垂直平分线的解析式;
的垂直平分线的解析式;
(3)如图2,取与线段![]() 等长的一根橡皮筋,端点分别固定在
等长的一根橡皮筋,端点分别固定在![]() 两处.用铅笔拉着这根橡皮筋使笔尖
两处.用铅笔拉着这根橡皮筋使笔尖![]() 在直线
在直线![]() 上方的抛物线上移动,动点
上方的抛物线上移动,动点![]() 将与
将与![]() 构成无数个三角形,这些三角形中是否存在一个面积最大的三角形?如果存在,求出最大面积,并指出此时
构成无数个三角形,这些三角形中是否存在一个面积最大的三角形?如果存在,求出最大面积,并指出此时![]() 点的坐标;如果不存在,请简要说明理由.
点的坐标;如果不存在,请简要说明理由.
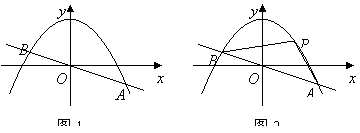 |
解:(1)解:依题意得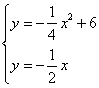 解之得
解之得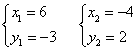
![]()
 (2)作
(2)作![]() 的垂直平分线交
的垂直平分线交![]() 轴,
轴,![]() 轴于
轴于![]() 两点,交
两点,交![]() 于
于![]() (如图1)
(如图1)
由(1)可知:![]()
![]()
![]()
过![]() 作
作![]() 轴,
轴,![]() 为垂足
为垂足
由![]() ,得:
,得:![]() ,
,
同理:![]()
设![]() 的解析式为
的解析式为![]()
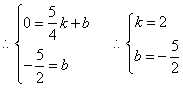
![]() 的垂直平分线的解析式为:
的垂直平分线的解析式为:![]() .
.
(3)若存在点![]() 使
使![]() 的面积最大,则点
的面积最大,则点![]() 在与直线
在与直线![]() 平行且和抛物线只有一个交点的直线
平行且和抛物线只有一个交点的直线![]() 上,并设该直线与
上,并设该直线与![]() 轴,
轴,![]() 轴交于
轴交于![]() 两点(如图2).
两点(如图2).
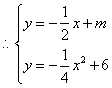
![]()
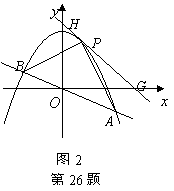
![]() 抛物线与直线只有一个交点,
抛物线与直线只有一个交点,
![]() ,
,
![]()
在直线![]() 中,
中,
![]()
![]()
设![]() 到
到![]() 的距离为
的距离为![]() ,
,
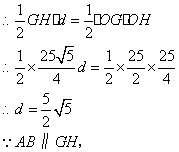
![]() 到
到![]() 的距离等于
的距离等于![]() 到
到![]() 的距离
的距离![]() .
.
![]()
![]()
![]()
32.已知:![]() 是方程
是方程![]() 的两个实数根,且
的两个实数根,且![]() ,抛物线
,抛物线![]() 的图像经过点A(
的图像经过点A(![]() )、B(
)、B(![]() ).
).
(1) 求这个抛物线的解析式;
(2)
设(1)中抛物线与![]() 轴的另一交点为C,抛物线的顶点为D,试求出点C、D的坐标和△BCD的面积;(注:抛物线
轴的另一交点为C,抛物线的顶点为D,试求出点C、D的坐标和△BCD的面积;(注:抛物线![]()
![]() 的顶点坐标为(
的顶点坐标为(![]() )
)
(3) 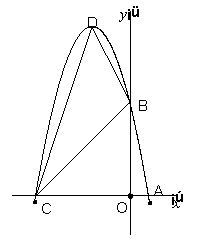 P是线段OC上的一点,过点P作PH⊥
P是线段OC上的一点,过点P作PH⊥![]() 轴,与抛物线交于H点,若直线BC把△PCH分成面积之比为2:3的两部分,请求出P点的坐标.
轴,与抛物线交于H点,若直线BC把△PCH分成面积之比为2:3的两部分,请求出P点的坐标.
解:(1)解方程![]() 得
得![]()
由![]() ,有
,有![]()
所以点A、B的坐标分别为A(1,0),B(0,5).
将A(1,0),B(0,5)的坐标分别代入![]() .
.
得![]() 解这个方程组,得
解这个方程组,得![]()
所以,抛物线的解析式为![]()
(2)由![]() ,令
,令![]() ,得
,得![]()
解这个方程,得![]()
所以C点的坐标为(-5,0).由顶点坐标公式计算,得点D(-2,9).
过D作![]() 轴的垂线交
轴的垂线交![]() 轴于M.
轴于M.
则![]()
![]() ,
,![]()
所以,![]() .
.
(3)设P点的坐标为(![]() )
)
因为线段BC过B、C两点,所以BC所在的值线方程为![]() .
.
那么,PH与直线BC的交点坐标为![]() ,
,
PH与抛物线![]() 的交点坐标为
的交点坐标为![]() .
.
由题意,得①![]() ,即
,即![]()
解这个方程,得![]() 或
或![]() (舍去)
(舍去)
②![]() ,即
,即![]()
解这个方程,得![]() 或
或![]() (舍去)
(舍去)
P点的坐标为![]() 或
或![]() .
.
33.已知二次函数图象的顶点在原点![]() ,对称轴为
,对称轴为![]() 轴.一次函数
轴.一次函数![]() 的图象与二次函数的图象交于
的图象与二次函数的图象交于![]() 两点(
两点(![]() 在
在![]() 的左侧),且
的左侧),且![]() 点坐标为
点坐标为![]() .平行于
.平行于![]() 轴的直线
轴的直线![]() 过
过![]() 点.
点.
(1)求一次函数与二次函数的解析式;
(2)判断以线段![]() 为直径的圆与直线
为直径的圆与直线![]() 的位置关系,并给出证明;
的位置关系,并给出证明;
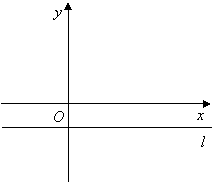 (3)把二次函数的图象向右平移
(3)把二次函数的图象向右平移![]() 个单位,再向下平移
个单位,再向下平移![]() 个单位
个单位![]() ,二次函数的图象与
,二次函数的图象与![]() 轴交于
轴交于![]() 两点,一次函数图象交
两点,一次函数图象交![]() 轴于
轴于![]() 点.当
点.当![]() 为何值时,过
为何值时,过![]() 三点的圆的面积最小?最小面积是多少?
三点的圆的面积最小?最小面积是多少?
解:(1)把![]() 代入
代入![]() 得
得![]() ,
,
![]() 一次函数的解析式为
一次函数的解析式为![]() ;
;
![]() 二次函数图象的顶点在原点,对称轴为
二次函数图象的顶点在原点,对称轴为![]() 轴,
轴,
![]() 设二次函数解析式为
设二次函数解析式为![]() ,
,
把![]() 代入
代入![]() 得
得![]() ,
,
![]() 二次函数解析式为
二次函数解析式为![]() .
.
|
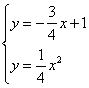
解得![]() 或
或![]() ,
,
![]() ,
,
过![]() 点分别作直线
点分别作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,
,
则![]() ,
,
![]() 直角梯形
直角梯形![]() 的中位线长为
的中位线长为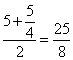 ,
,
过![]() 作
作![]() 垂直于直线
垂直于直线![]() 于点
于点![]() ,则
,则![]() ,
,![]() ,
,
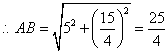 ,
,
![]()
![]() 的长等于
的长等于![]() 中点到直线
中点到直线![]() 的距离的2倍,
的距离的2倍,
![]() 以
以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切.
相切.
(3)平移后二次函数解析式为![]() ,
,
令![]() ,得
,得![]() ,
,![]() ,
,![]() ,
,
![]() 过
过![]() 三点的圆的圆心一定在直线
三点的圆的圆心一定在直线![]() 上,点
上,点![]() 为定点,
为定点,
![]() 要使圆面积最小,圆半径应等于点
要使圆面积最小,圆半径应等于点![]() 到直线
到直线![]() 的距离,
的距离,
此时,半径为2,面积为![]() ,
,
设圆心为![]() 中点为
中点为![]() ,连
,连![]() ,则
,则![]() ,
,
在三角形![]() 中,
中,![]() ,
,
![]() ,而
,而![]() ,
,![]() ,
,
![]() 当
当![]() 时,过
时,过![]() 三点的圆面积最小,最小面积为
三点的圆面积最小,最小面积为![]() .
.