二次函数练习卷
一、选择题:
1、二次函数y=x2-(12-k)x+12,当x>1时,y随着x的增大而增大,当x<1时,y随着x的增大而减小,则k的值应取( )
(A)12 (B)11 (C)10 (D)9
2、下列四个函数中,y的值随着x值的增大而减小的是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
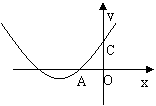 3、抛物线y=ax2+bx+c的图象如图,OA=OC,则 ( )
3、抛物线y=ax2+bx+c的图象如图,OA=OC,则 ( )
(A) ac+1=b (B) ab+1=c (C)bc+1=a (D)以上都不是
4、若二次函数y=ax2+bx+c的顶点在第一象限,且经过点(0,1),(-1,0),则S=a+b+c的变化范围是 ( )
(A) 0<S<2 (B) S>1 (C) 1<S<2 (D)-1<S<1
5、如果抛物线y=x2-6x+c-2的顶点到x轴的距离是3,那么c的值等于( )
(A)8 (B)14 (C)8或14 (D)-8或-14
6、把二次函数![]() 的图象向左平移2个单位,再向上平移1个单位,所得到的图象对应的二次函数关系式是( )
的图象向左平移2个单位,再向上平移1个单位,所得到的图象对应的二次函数关系式是( )
(A)![]() (B)
(B) ![]() (C)
(C) ![]()
(D)![]()
7、(3)已知抛物线y=ax2+bx,当a>0,b<0时,它的图象经过( )
A.一、二、三象限 B.一、二、四象限
C.一、三、四象限 D.一、二、三、四象限
8、若![]() ,则二次函数
,则二次函数![]() 的图象的顶点在 ( )
的图象的顶点在 ( )
(A)第一象限(B)第二象限(C)第三象限(D)第四象限
9、已知二次函数![]() ,
,![]() 为常数,当y达到最小值时,x的值为 ( )
为常数,当y达到最小值时,x的值为 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
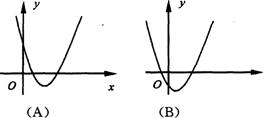 10、当a>0, b<0,c>0时,下列图象有可能是抛物线y=ax2+bx+c的是( )
10、当a>0, b<0,c>0时,下列图象有可能是抛物线y=ax2+bx+c的是( )
二、填空题:(28分)
11、已知二次函数y=ax2(a≥1)的图像上两点A、B的横坐标分别是-1、2,点O是坐标原点,如果△AOB是直角三角形,则△OAB的周长为 。
12、已知二次函数y=-4x2-2mx+m2与反比例函数y=![]() 的图像在第二象限内的一个交点的横坐标是-2,则m的值是 。
的图像在第二象限内的一个交点的横坐标是-2,则m的值是 。
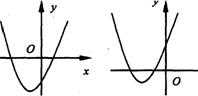
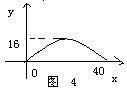
13、有一个抛物线形拱桥,其最大高度为16m,跨度为40m,现把它的示意图放在平面直角坐标系中如 图(4),求抛物线的解析式是_______________。
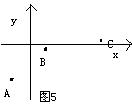
14、如图(5)A. B. C.是二次函数y=ax2+bx+c(a≠0)的图像上三点,根据图中给出的三点的位置,可得a-.——0,c——0, 15、老师给出一个函数,甲,乙,丙,丁四位同学各指出这个函数的一个性质:甲:函数的图像不经过第三象限。
乙:函数的图像经过第一象限。丙:当x<2时,y随x的增大而减小。丁:当x<2时,y>0,已知这四位同学叙述都正确,请构造出满足上述所有性质的一个函数___________________。
16、已知二次函数y=x2+bx+c的图像过点A(c,0),且关于直线x=2对称,则这个二次函数的解析式可能是————————————(只要写出一个可能的解析式)
17、炮弹从炮口射出后,飞行的高度h(m)与飞行的时间t(s)之间的函数关系是h=v0tsinα—5t2,其中v0是炮弹发射的初速度, α是炮弹的发射角,当v0=300(![]() ), sinα=
), sinα=![]() 时,炮弹飞行的最大高度是___________。
时,炮弹飞行的最大高度是___________。
18.已知点P (a,m)和Q( b,m)是抛物线y=2x2+4x-3上的两个不同点,则a+b=_______.
19.已知二次函数![]() 的图象与x轴交于点(-2,0),(x1,0)且1<x1<2,与y·轴正半轴的交点在点(0,2)的下方,下列结论:①a<b<0;②2a+c>0;③4a+c< 0,④2a-b+l>0.其中的有正确的结论是(填写序号)__________.
的图象与x轴交于点(-2,0),(x1,0)且1<x1<2,与y·轴正半轴的交点在点(0,2)的下方,下列结论:①a<b<0;②2a+c>0;③4a+c< 0,④2a-b+l>0.其中的有正确的结论是(填写序号)__________.
三、解答题:
20.将进货单价为40元的商品按50元售出时,就能卖出500个,已知这个商品每个涨价1元,其销售量就减少10个。 (1)问:为了赚得8000元的利润,售价应定为多少?这时进货多少个? (2)当定价为多少元时,可获得最大利润?
21.已知y是x的二次函数,且其图象在x轴上截得的线段AB长4个单位,当x=3时,y取得最小值-2。(1)求这个二次函数的解析式 (2)若此函数图象上有一点P,使ΔPAB的面积等于12个平方单位,求P点坐标。
22.已知直线![]() 与x轴交于点A,与y轴交于点B;一抛物线的解析式为
与x轴交于点A,与y轴交于点B;一抛物线的解析式为![]() .
.
(1)若该抛物线过点B,且它的顶点P在直线![]() 上,试确定这条抛物线的解析式;
上,试确定这条抛物线的解析式;
(2)过点B作直线BC⊥AB交x轴交于点C,若抛物线的对称轴恰好过C点,试确定直线![]() 的解析式.
的解析式.
23.已知抛物线![]() 与x轴交于A、 B两点,与y轴交于点C.是否存在实数a,使得△ABC为直角三角形.若存在,请求出a的值;若不存在,请说明理由.
与x轴交于A、 B两点,与y轴交于点C.是否存在实数a,使得△ABC为直角三角形.若存在,请求出a的值;若不存在,请说明理由.
24.如图,已知抛物线![]() 与坐标轴交于
与坐标轴交于![]() 三点,点
三点,点![]() 的横坐标为
的横坐标为![]() ,过点
,过点![]() 的直线
的直线![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是线段
是线段![]() 上的一个动点,
上的一个动点,![]() 于点
于点![]() .若
.若![]() ,且
,且![]() .
.
(1)确定![]() 的值:
的值:
(2)写出点![]() 的坐标(其中
的坐标(其中![]() 用含
用含![]() 的式子表示):
的式子表示):
(3)依点![]() 的变化,是否存在
的变化,是否存在![]() 的值,使
的值,使![]() 为等腰三角形?若存在,求出所有
为等腰三角形?若存在,求出所有![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
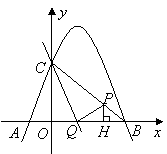
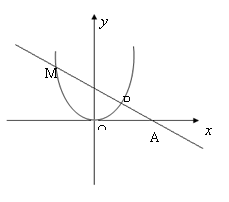
25.已知P(![]() ,
,![]() )是抛物线
)是抛物线![]() 上的点,且点P在第一象限.
上的点,且点P在第一象限.
(1)求![]() 的值
的值
(2)直线![]() 过点P,交
过点P,交![]() 轴的正半轴于点A,交抛物线于另一点M.
轴的正半轴于点A,交抛物线于另一点M.
①当![]() 时,∠OPA=90°是否成立?如果成立,请证明;如果不成立,举出一个反例说明;
时,∠OPA=90°是否成立?如果成立,请证明;如果不成立,举出一个反例说明;
 ②当
②当![]() 时,记△MOA的面积为S,求
时,记△MOA的面积为S,求![]() 的最大值
的最大值
.
参考答案
一、CBAAC,DBDBA
二、11.![]() 12。-7 13。
12。-7 13。![]()
14.![]() 15。
15。![]() 不唯一
不唯一
16.![]() 17。1125米 18。-2 19。①②③④
17。1125米 18。-2 19。①②③④
20.(1)60元,400个或80元200个 (2)70
21.解:(1)∵当x=3时 y取得最小值-2.即抛物线顶点为(3,-2).∴设二次函数解析式为
y=a(x-3)2-2
又∵图象在x轴上截得线段AB的长是4,∴图象与x轴交于(1,0)和(5,0)两点
∴a(1-3)2-2=0 ∴a=![]()
∴所求二次函数解析式为y=![]() x2-3x+
x2-3x+![]()
(2)∵ΔPAB的面积为12个平方单位,|AB|=4
∴![]() ×4×|Py|=12 ∴|Py|=6 ∴Pg=±6
×4×|Py|=12 ∴|Py|=6 ∴Pg=±6
但抛物线开口向上,函数值最小为-2,∴Py=-6应舍去,∴Pg=6 又点P在抛物线上,
∴6=![]() x2-3x+
x2-3x+![]() x1=-1,x2=7
x1=-1,x2=7
即点P的坐标为(-1,6)或(7,6)
22.解:(1)![]() 或
或![]()
将![]() 代入,得
代入,得![]() .顶点坐标为
.顶点坐标为![]() ,由题意得
,由题意得![]() ,解得
,解得![]() .
.
(2)![]()
23. 由![]() ,解得
,解得 ![]() ,
,![]() .
.
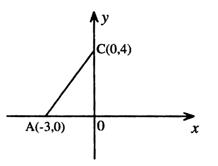 ∴ 点A、B的坐标分别为(-3,0),(
∴ 点A、B的坐标分别为(-3,0),(![]() ,0).
,0).
∴ ![]() ,
,![]() ,
,
![]()
![]() .
.
∴ ![]() ,
,
![]() ,
,![]() .
.
〈ⅰ〉当![]() 时,∠ACB=90°.
时,∠ACB=90°.
由![]() ,
,
得![]() .
.
解得 ![]() .
.
∴ 当![]() 时,点B的坐标为(
时,点B的坐标为(![]() ,0),
,0),![]() ,
,![]() ,
,![]() .
.
于是![]() .
.
∴ 当![]() 时,△ABC为直角三角形.
时,△ABC为直角三角形.
〈ⅱ〉当![]() 时,∠ABC=90°.
时,∠ABC=90°.
24.[解] (1)![]()
![]() (2)
(2)![]()
![]()
![]()
(3)存在![]() 的值,有以下三种情况
的值,有以下三种情况
①当![]() 时
时 ![]() ,则
,则![]()

![]()
![]()
②当![]() 得
得![]()
![]()
 ③当
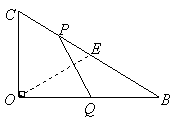
③当![]() 时,如图
时,如图
解法一:过![]() 作
作![]() ,又
,又![]()
则![]() 又
又![]()
![]()
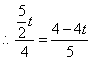
![]()
解法二:作![]() 斜边中线
斜边中线![]() 则
则![]() ,
,
此时![]()
![]()
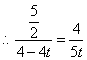
![]()
 解法三:在
解法三:在![]() 中有
中有![]()
![]()
![]()
![]() (舍去) 又
(舍去) 又![]()
![]() 当
当![]() 或
或![]() 或
或![]() 时,
时,![]() 为等腰三角形.
为等腰三角形.
25.[解] (1)![]()
![]()
(2)①b=2a,![]() P在直线上,则
P在直线上,则
![]()
![]()
![]() A(2,0)
A(2,0)
![]()
M(-1,a) ∠OPA=90° 即![]() ,
,![]()
![]() ,
,![]() P(1,1)
P(1,1)
故存在这样的点P
②![]() 又
又![]()
![]()
∴S=![]()
![]()
∴当![]() 时,
时,![]()