中考数学模拟试卷44
班级 姓名 座号 成绩
(满分150分；考试时间120分钟)
一、填空题：(每小题3分，共30分)
1．据新华社报道：2010年我国粮食产量将达到千克，用科学记数法可表示为_______________千克.
2．若
+y+1=0，则x2005+y2006=_____________．
3．如图，一个透明的圆柱形状的玻璃杯，由内部测得其底面半径为3cm，高为8cm，今有一支12cm的吸管任意斜放于杯中，若不考虑吸管的粗细，吸管露出杯口长度最少为__________cm．
4．若a+
=6，则a2+
=______________．
5．某商场5月份一周的利润情况如下表：
| 日期 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 | 8日 |
| 当日利润／万元 | 0.20 | 0.24 | 0.23 | 0.23 | 0.2l | 0.19 | O.17 |
根据上表，估计该商场今年5月份的总利润是_________万元．
6．已知
=
，则
=______________.
7．一顶简易的圆锥形帐篷，帐篷收起来时伞面的长度有4米，撑开后帐篷高2米，则帐篷撑好后的底面直径是______________米.
8．在Rt△ABC中，∠C=900，AC=6，BC=8，则其外接圆的半径为______________．
9．圆心在x轴上的两圆相交于A、B两点，已知A点的坐标为(-3，2)，则B点的坐标是____．
10．用长4cm，宽3cm的邮票300枚不重不漏摆成一个正方形，这个正方形的边长等于____cm．
二、选择题：(每题3分，共30分)
11．元月份某一天，北京市的最低气温为-6 0C，常州市的最低气温为2 0C，那么这一天常州市的气温比北京市的最低气温高
A．6 0C B．4 0C C．-8 0C D．8 0C
12．如图，有一个正方体纸盒，在它的三个侧面分别画有三角形、正方形和圆，现用一把剪刀沿着它的棱剪开成一个平面图形，则展开图可以是
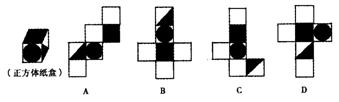
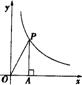13．学校开展为贫困地区捐书活动，以下是八名学生捐书的册数：2，2，2，3，6，5，6，7，则这组数据的中位数为
A．2 B．3 C．4 D．4.5
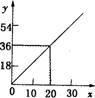
14.如图，P是反比例函数y=
在第一象限分支上的一个动点，PA⊥x轴，随着x的逐渐增大，△AP0的面积将
A．增大 B．减小 C．不变 D．无法确定
15.为了鼓励节约用水,按以下规定收取水费：(1)每户每月用水量不超过20立方米，则每立方米水费1.8元；(2)若每户每月用水量超过20立方米，则超过部分每立方米水费3元，设某户一个月所交水费为y(元)，用水量为x(立方米),则y与x的函数关系用图象表示为
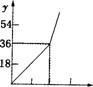
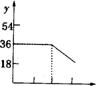
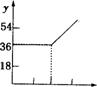
0 10 20 30 0 10 20 30 0 10 20 30
A B C D
16.一张桌子上摆放着若干个碟子，从三个方向上看，三种视图如下图所示，则这张桌手上共有碟子为
A.6个 B．9个 C．12个 D．17个
17．生物学指出：生态系统中，每输入一个营养级的能量，大约只有10％的能量能够滚动到下一个营养级，在H1→H2→H3→H4→H5→H6这条生物链中(Hn表示第n个营养级，n=1，2，…，6)．要使H6获得10千焦的能量，那么需要H1提供的能量约为
A．104千焦 B．105千焦 C．106千焦 D．107千焦
18．在1000个数据中，用适当的方法抽取50个作为样本进行统计，频数分布表中，54.5∽57.5这一组的频率是O.12，那么，估计总体数据落在54.5∽57.5之间的约有
A．6个 B．12个 C．60个 D．120．个
19．若不等式组
的解集是x>3，则m的取值范围是
A. m>3 B．m≥3 C．m≤3 D．m<3
20．如图，一个等边三角形的边长和与它的一边相外切的圆的周长相等，当这个圆按箭头方向从某一位置沿等边三角形的三边做无滑动旋转，直至回到原出发位置时，则这个圆共转了
A．4圈 B．3圈 C．5圈 D．3.5圈
三、解答题：(每题10分,共20分)
2l.计算：(
-
)0+(
)-2+
-9tan300．
22．解方程：
-
=1．
四、(23题10分，24题8分，共18分)
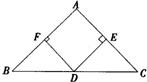
23．已知：如图，D是ΔABC的BC边上的中点，DE⊥AC，DF⊥AB，垂足分别是E、F，且BF=CE．
求证：(1)ΔABC是等腰三角形；
(2)当∠A=900时，试判断四边形AFDE是怎样的四边形，证明你的结论．
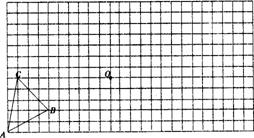24．在如图的12×24的方格纸中(每个小方格的边长都是1个单位)有一个ΔABC．现先把ΔABC向右平移8个单位、向上平移3个单位后得到ΔA1B1C1；再以点O为旋转中心把ΔA1B1C1按顺时针方向旋转900得到ΔA2B2C2，请在所给的方格纸中作出ΔA1B1C1和ΔA2B2C2．
五、(25、26题12分，27、28题14分，共52分)
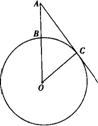25．如图，已知⊙O的半径为8 cm，点A是半径OB延长线上的一点，射线AC切⊙O于点C，弧BC的长为
cm，求线段AB的长(精确到0.01 cm)．
26．某校射击队在相同的条件下对甲乙两名运动员进行了10次射靶测试，成绩如下：
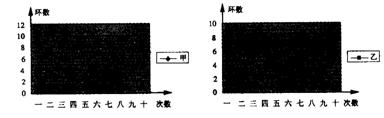
(1)请根据图中信息完成下表：
| 项目 | 平均数 | 中位数 | 方差 | 6.5—7.5环的频数 | 6．5--7.5环的频率 |
| 甲 | 7 | 4.2 | 0.2 | ||
| 乙 | 7 | 4 |
(2)甲、乙两人谁射靶的成绩比较稳定?请说明理由．
27．某产品每件成本10元，试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表：
| x(元) | 15 | 20 | 30 | … |
| y(件) | 25 | 20 | 10 | … |
若日销售量y是销售价x的一次函数．
(1)求出日销售量y(件)与销售价x(元)的函数关系式；
(2)要使每日的销售利润最大，每件产品的销售价应定为多少元?此时每日销售利润是多少元?
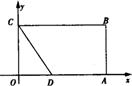
28．如图，在矩形OABC中，OA=8，OC=4，OA、OC分别在x，y轴上，点0在OA上，且CD=AD,
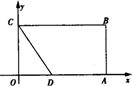(1)求直线CD的解析式；
(2)求经过B、C、D三点的抛物线的解析式；
(3)在上述抛物线上位于x轴下方的图象上，是否存在一点P，使ΔPBC的面积等于矩形的面积?若存在，求出点P的坐标，若不存在请说明理由．
参考答案
1. 5.4×1011
2. 0 此题主要考查二次根式和绝对值的非负性．
3. 2 此图正好构成一个直角三角形，直角边分别是6、8．则靠在杯上的斜边为10，故露出杯口的长度为2cm．
4. 34 把a+=6两边分别平方即可．
5. 6.3 先算出一天的平均利润，再乘以30即可．
6. 
本题考查了比例的性质．
7．4 此题主要考查了直角三角形的知识，斜边是4米，一条直角边是2米，其底面半径是另一条直角边．可通过勾股定理求得，最后乘以2即可．
8．5 直角三角形的外接圆半径等于其斜边的一半，斜边可由勾股定理求得．
9．(-3，-2) 由题意可知，A、B关于x轴对称，故其坐标为(-3，-2)．
10．60 一张邮票的面积是12cm2，300张邮票的面积就为3600cm2，也就是正方形的面积为3600cm2，设该正方形的边长为xcm，则x2=3600．解得x=60.
11．D 列式为：2-(-6)=8．
12．C 由图可知，正方形和圆应在一面上，三角形在另一面上，故选C．
13. C 中位数就是把所有的数据按照从大到小的顺序排列后，取中间一个或两个数的平均数．
14．C 此三角形的面积等于xy的一半，恒为3．
15．D 20立方米内是一次函数,20立方米外也是一次函数，但是变化越来越明显，故选D．
16．C 俯视图说明有三摞，主视图说明两摞，左视图说明两摞，故选C．
17. C 设H1的能量x千焦，则有(10％)5x=1O，解得x=106，故选C．
18．D 可列式为1000÷50×50×O.12=120．
19．C 解不等式组可得x>3，x>m，因为已知其解集为x>3，依据同大取大法则，m≤3，故选C．
20． A ⊙O从与AC相切于A点滚动到与AB相切于A点，转过1200，则在三个顶点共转过3600，即一周．又因为⊙O在三边上各转过一周，所以共转动了4周．
21．原式=1+9+3-9×
=10．
22． 6-3(x+1)=x2-1，x2+3x-4=0，∴xl=-4，x2=1．经检验：xl=-4是原方程的根.
23．(1)∵BD=CD，BF=CE，∴RtΔBDF≌RtΔCDE，∴∠B=∠C．
ΔABC是等腰三角形．
(2)∵∠A=900，DE⊥AC；DF⊥AB,∴四边形AFDE是矩形，
又∵RtΔBDF≌RtΔCDE,∴DF=DE，∴四边形AFDE是正方形．
24．图略．
25．∵
=
,∴n=50，∴∠BOC=500，∵AC切0于C，
∴OC⊥AC，∴OA=
≈12.45，∴AB=OA-OB=4.45(m)．
26．(1)甲：7．5，2；乙：7，1.2，0.4．
(2)∵
>
．∴乙运动员的射靶成绩较为稳定．
27．(1)设此一次函数解析式为y=kx+b,则
,∴k=-1,b=40,
即：一次函数解析式为y=-x+40.
(2)设每件产品的销售价应定为x元，所获销售利润为w元，
w=(x-10)(40-x)=-x2+50x-400=-(x-25)2+225,
产品的销售价应定为25元，此时每日获得最大销售利润为225元．
28．(1)设OD=x,则CO=AD=8-x.
∴(8-x)2-x2=16．∴x=3，D的坐标是(3，O)，
又点C的坐标是(0,4)，设直线CD的解析式为y=kx+b,
于是有
,∴y=-
x+4.
(2)由题意得B、C,D三点坐标分别为(8，4)，(0,4)．(3，O)，设抛物线解析式为y=ax2+bx+c
则有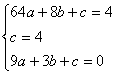
于是可得抛物线解析式为：y=
x2-
x+4．
(3)在抛物线上不存在一点P，使ΔPBC的面积等于矩形ABCD的面积．
理由是：由抛物线的对称性可知．以抛物线顶点为P的ΔPBC面积为最大.
由y=x2-x+4= (x-4)2-可却，顶点坐标为(4，-)．则ΔPBC的高为4+-=
.
∴ΔPBC的面积为
×8×=
小于矩形ABCD的面积为4×8=32．
故在x轴下方且在抛物线上不存在一点P，使ΔPBC的面积等于矩形ABCD的面积.