初中数学总复习（18）四边形、平行四边形、梯形
〖考试内容〗
多边形，多边形的内角和与外角和，正多边形，平行四边形，梯形的概念、条件及性质， 平面图形的镶嵌.
〖考试要求〗
①了解多边形的内角和与外角和公式，了解正多边形的概念，了解四边形的不稳定性.
②掌握平行四边形的概念和性质，掌握四边形是平行四边形的条件.
③梯形的概念和性质，掌握等腰梯形的有关性质，掌握四边形是等腰梯形的条件.
④通过探索平面图形的镶嵌，知道任意一个三角形、四边形或正六边形可以镶嵌平面，并能运用这几种图形进行简单的镶嵌设计.
〖考点复习〗
1．多边形的内角和与外角和
[例1] 正n边形的内角和等于 1080°，那么这个正n边形的边数n=_____.
[例2]一个多边形的每一个外角都等于72°,这个多边形是（ ）
A、正三角形 B、正方形
C、正五边形 D、正六边形
2．图形的密铺
[例3]某城市进行旧城区人行道的路面翻新,准备对地面密铺彩色地砖, 有人提出了4种地砖的形状供设计选用：①正三角形，②正四边形，③正五边形，④正六边形．其中不能进行密铺的地砖的形状是（ ）.
A、① B、② C、③ D、④
3．平行四边形的性质和判定
[例4如图，已知□ABCD中，E为AD的中点，CE的延长线交BA的延长线于点E。
⑴求证：CD＝FA；
⑵若使∠F＝∠BCF，□ABCD的边长之间还需再添加一个什么条件？
请你补上这个条件，并进行证明(不要再增添辅助线)。
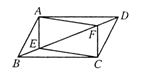[例5]如图，E、F是□ABCD对角线BD上的两点，请你添加一个适当的条件：＿＿＿＿＿＿，使四边形AECF是平行四边形。
4．梯形和等腰梯形的性质和判定
[例6]如图,请写出等腰梯形ABCD，（AB∥CD）特有而一般梯形不具有的三个特征：＿＿＿＿＿＿＿；＿＿＿＿＿＿＿；＿＿＿＿＿＿＿＿＿。
[例7] 如图，梯形ABCD中，AD∥BC，AB＝DC，∠ADC＝120°，对角线CA平分∠DCB，E为BC的中点，试求△DCE与四边形ABED面积的比．
〖考题训练〗
1．正六边形的一个内角的度数是___________º
2．已知一个五边形的4个内角都是
，则第5个内角的度数是 ．
3．使用同一种规格的下列地砖，不能密铺的是（ ）
A、正六边形地砖 B、正五边形地砖
C、正方形地砖 D、正三角形地砖
4．如果要用正三角形和正方形两种图形进行密铺，那么至少需要（）
A、 三个正三角形，两个正方形
B 、两个正三角形，三个正方形
C 、两个正三角形，两个正方形
D 、三个正三角形，三个正方形
5．用同一种正多边形地砖镶嵌成平整的地面，那么这种正多边形地砖的形状可以是 . （只需写出一种即可）
6．下列命题中，正确的是（ ）
A、同位角相等 B、平行四边形的对角线互相垂直平分
C、等腰梯形的对角线互相垂直
D、矩形的对角线互相平分且相等
7．已知：如图，平行四边形ABCD中，E、F分别是边BC和AD上的点，且BE=DF，求证：AE=CF.
8．如图，E、F是四边形ABCD的对角线AC上的两点，AF=CE，DF=BE，DF∥BE。
求证：（1）⊿AFD≌⊿CEB
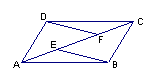（2）四边形ABCD是平行四边形。
9．已知：在等腰梯形ABCD中，AD∥BC，对角线AC⊥BD；AD=3cm，BC=7cm，则梯形的高是_______cm。
10．有一个直角梯形零件ABCD，AD∥BC，斜腰DC的长为10cm，∠D=120°，则该零件另一腰AB的长是 cm（结果不取近似值）
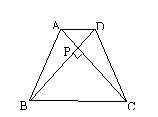11．已知：如图，等腰梯形ABCD中，AD∥BC，对角线AC⊥BD且相交于点P，AD=3cm,BC=7cm，利用上述的性质求梯形的面积.
12．如图，在
中，
，
是的中位线，点
在
延长上，且
．求证：四边形
是等腰梯形．
 |
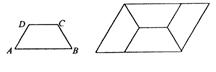
13．如图甲，四边形ABCD是等腰梯形，AB∥DC．由4个这样的等腰梯形可以拼出图乙所示的平行四边形.
（1）求四边形ABCD四个内角的度数；
（2）试探究四边形ABCD四条边之间存在的等量关系，并说明理由；
（2）现有图甲中的等腰梯形若干个，利用它们你能拼出一个菱形吗?若能，请你画出大致的示意图．
 |
〖课后作业〗
1．若n边形的内角和是1260º，则边数n为（ ）
A、8 B、9 C、10 D、11
2．如果正多边形的一个外角为72º，那么它的边数是＿＿＿＿＿＿。
3．某商店出售下列形状的地板砖：①正三角形；②正方形；③正五边形；④正六边形.如果只限于用一种地板砖镶嵌地面，那么不能选购的地板砖序号是________．
4．下列命题中，真命题是（ ）
A、一组对边平行且有一组邻边相等的四边形是平行四边形
B、顺次连结四边形各边中点所得到的四边形是矩形
C、等边三角形既是轴对称图形又是中心对称图形
D、对角线互相垂直平分的四边形是菱形
5．等腰梯形是________对称图形.
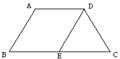6．如图，等腰梯形ABCD中，AD∥BC，AD=5，AB=6，BC=8，且AB∥DE，△DEC的周长是（ ）
A、3 B、12 C、15 D、19
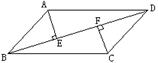7．如图，平行四边形ABCD中，AE⊥BD，CF⊥BD，垂足分别为E、F。
（1）写出图中每一对你认为全等的三角形；
（2）选择（1）中的任意一对进行证明。
8．（本小题满分5分）
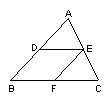
如图，在△ABC中，点D、E、F、分别在AB、AC、BC上，DE//BC，且F是BC的中点．
求证：DE=CF
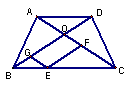9．如图，已知在梯形ABCD中，AD∥BC，AB = DC，对角线AC和BD相交于点O，E是BC边上一个动点（E点不与B、C两点重合），EF∥BD交AC于点F，EG∥AC交BD于点G.
⑴求证：四边形EFOG的周长等于2 OB；
⑵请你将上述题目的条件“梯形ABCD中，AD∥BC，AB = DC”改为另一种四边形，其他条件不变，使得结论“四边形EFOG的周长等于2 OB”仍成立，并将改编后的题目画出图形，写出已知、求证、不必证明.
10．请将四个全等直角梯形(如图)，拼成一个平行四边形，并画出两种不同的拼法示意图(拼出的两个图形只要不全等就认为是不同的拼法)．
