初中数学总复习次方程（组）

（6）一次方程（组）

〖考试内容〗

方程和方程的解，一元一次方程及其解法，二元一次方程组及其解法.

〖考试要求〗

①会解一元一次方程、简单的二元一次方程组.

②会用观察、画图或计算器等手段估计方程的解.

〖考点复习〗

1.方程的解

[例1] 方程x(x+3)=x+3的解是 （　）

A、 x=1　　　　B、 x₁=0, x₂=-3

C、x₁=1, x₂=3　　D、 x₁=1, x₂=-3

2. 会解一元一次方程、简单的二元一次方程组.

[例2]解方程：

[例3] 解方程组

3．方程估解

[例4]已知方程x²＋2x－5＝0有一正一负的两个实数解，其中正实数解所在的范围是（　　 ）

A、0＜x≤1　　　　 B、1＜x≤2　　

C、 2＜x≤3　　　　D、 3＜x≤4

4.列方程

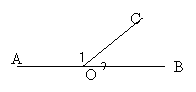[例5]如图，点O在直线AB上，OC为射线，比的3倍少，设，的度数分别为,,那么下列求出这两个角的度数的方程是（　）

A、　　 B、

C、　　 D、

〖考题训练〗

1．下列各数中，适合方程 的一个近似值（精确到0.1）是 （　 ）

　　A、1.5　　B、1.6　　C、1.7　　 D、1.8

3．（2005盐城）若一个二元一次方程的解为，则这个方程可以是_________________（只要求写出一个）。

3．方程的解是（ ）

　　A、1　　 B、－1　　　C、±1　　　D、0

4．（2004深圳）图8是2004年6月份的日历，如图中那样，用一个圈竖着圈住3个数．如果被圈的三个数的和为39，则这三个数中最大的一个为　　　　 ．

日	一	二	三	四	五	六
		1	2	3	4	5
6	7	8	9	10	11	12
13	14	15	16	17	18	19
20	21	22	23	24	25	26
27	28	29	30

5．若实数m,n满足条件m+n=3，且m-n=1，则m=________，n=___________.

6．解方程组：

7．解方程组：

　

8．解方程组：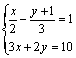

9．已知关于x的方程的解是x=2，其中a≠0且b≠0，求代数式的值 。

〖课后作业〗

1．方程x²(x－1)=0的根是（　）

　　　 A、0　　 B、1　 C、0，－1　　D、0，1

2．如图是一个数表，现用一个矩形在数表中任意框出4个数则

（1）a、c的关系是：__________________；

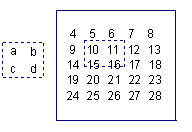（2）当a＋b＋c＋d＝32时，a＝__________．

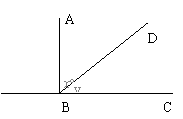
3．如图3，AB⊥BC，∠ABD的度数比∠DBC的度数的两倍少15°，设∠ABD和∠DBC的度数分别为x、y，那么下面可以求出这两个角的度数的方程组是（　 ）

A、　　 B、　

C、　　 D、

4．根据下列表格的对应值：

x	3.23	3.24	3.25	3.26
	－0.06	－0.02	0.03	0.09

判断方程＝0 (a≠0，a，b，c为常数)一个解x的范围是（　）

A、3＜x＜3.23 　　 B、3.23＜x＜3.24

C、3.24＜x＜3.25 　 D、3.25 ＜x＜3.26　

5．解方程组：

6．解方程组