初中数学总复习（16）点、线、面、角.
〖考试内容〗
点、线、面、角、角平分线及其性质.
补角，余角，对顶角.垂线，点到直线的距离，线段垂直平分线及其性质.平行线，两直线平行的性质.
〖考试要求〗
①在实际背景中认识，理解点、线、面、角的概念.
②会比较角的大小，能估计一个角的大小，会计算角度的和与差，认识度、分、秒，会进行简单换算.
③了解角平分线及其性质.
④了解补角、余角、对顶角，知道等角的余角相等、等角的补角相等、对顶角相等.
⑤了解垂线、垂线段等概念，了解垂线段最短的性质，理解点到直线距离的意义.
⑥知道过一点有且仅有一条直线垂直于已知直线，会用三角尺或量角器过一点画一条直线垂线.
⑦了解线段垂直平分线及其性质.
⑧了解平行线的概念及平行线基本性质.
⑨知道过直线外一点有且仅有一条直线平行于已知直线，会用三角尺和直尺过已知直线外一点画这条直线的平行线.
〖考点复习〗
1．角的度量
[例1]在七巧板拼图中（如图1），∠ABC=＿＿＿度 .
2．余角和补角
[例2]5．已知∠α= 50°，那么它的补角等于________________°.
3．平行线的性质
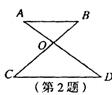[例3]如图，AB∥CD，AD，BC相交于O，∠BAD=35°，∠BOD=76°，则∠C的度数是( )
(A) 31° (B) 35°
(C) 41° (D) 76°
4．角平分线性质
[例4] 如图，P是∠AOB的平分线上的一点，PC⊥AO于C，PD⊥OB于D，写出图中一组相等的线段 （只需写出一组即可）
〖考题训练〗
1．我们知道，五星红旗上有五颗五角星，每一颗五角星有五个相等的锐角(如图)，每个锐角等于
A、30o B、36o
C、45o D、60o
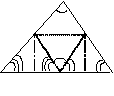2．亲爱的同学们，在我们的生活中处处有数学的身影.请看图，折叠一张三角形纸片，把三角形的三个角拼在一起，就得到一个著名的几何定理，请你写出这一定理的结论：“三角形的三个内角和等于_______°.”
3．图中物体的形状类似于（ ）.
A、棱柱 B、圆柱 C、圆锥D、球
4．若∠
=30°，则∠的补角是（
）
A、30° B、60°
C、120° D、150°
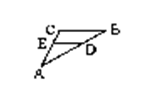
5．在△ABC中，D、E分别是AB、AC边上的点，DE∥BC，∠ADE＝30º，∠C＝120º，则∠A＝（ ）
A．60º B．45º C． 30º D． 20º
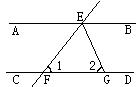6．如图，AB∥CD，直线EF分别交AB、CD于点E、F，EG平分∠BEF交CD于点G，∠1=50°，求∠2的度数。
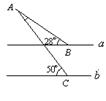
7．如图所示，直线a∥b，则∠A= ▲ 度．
8. (本题满分10分) 如图6，已知：在直角△ABC中，∠C＝90°，
BD平分∠ABC且交AC于D.
（1）若∠BAC＝30°，求证: AD＝BD；
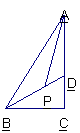（2）若AP平分∠BAC且交BD于P，求∠BPA的度数.
9．如图，在△ABC中，ÐC=90º，AC=8cm，AB的垂直平分线MN交AC于D，连结BD，若cos∠BDC=
，则BC的长是（ ）
A、4cm B、6cm C、8cm D、10cm
10．下列图中能过说明∠1>∠2的是 ( )
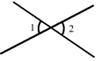
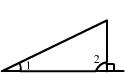
A. B.
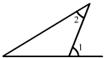
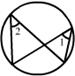
C. D.
〖课后作业〗
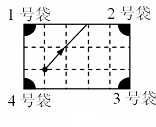
1．图3是一个经过改造的台球桌面的示意图，图中四个角上的阴影部分分别表示四个入球孔.如果一个球按图中所示的方向被击出（球可以经过多反射），那么该球最后将落入的球袋是
A．1 号袋 B．2 号袋 C．3 号袋 D．4号袋
2．已知：∠A＝30°,则∠A的补角是_____度.
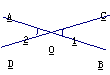3．如图，直线AB、CD相交于点O，若∠1=28°,则∠2= .
4．如图，在平行四边形ABCD中，下列各式不一定正确的是
A
B．
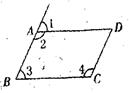C．
D．
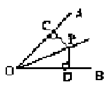5．如图，OP平分∠AOB，PC⊥OA于C，PD⊥OB于D，则PC与PD的大小关系（ ）
A．PC＞PD B．PC＝PD
C． PC＜PD D． 不能确定
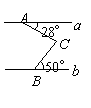
6．如图，直线a∥b，则∠ACB=_______.