（19）矩形、菱形、正方形
〖考试内容〗
矩形，菱形，正方形，的概念、条件及性质.
〖考试要求〗
①掌握矩形、菱形、正方形的概念和性质，了解它们之间的关系.
②掌握四边形是矩形、菱形、正方形的条件.
〖考点复习〗
1. 矩形的性质和判定
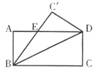[例1]如图，将矩形ABCD沿对角线BD折叠，使C落在C＇处，BC＇交AD于E，则下列结论不一定成立的是（ ）
A、AD＝BC＇ B、∠EBD＝∠EDB
C、△ABE∽△CBD D、
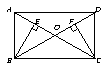[例2] 如图，矩形ABCD中，AC与BD交于O点，BE⊥AC于E，CF⊥BD于F.
求证：BE=CF.
2. 菱形的性质和判定
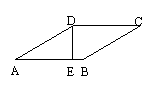[例3] 如图，在菱形ABCD中，DE⊥AB，垂足是E，DE＝6， sinA=
,则菱形ABCD的周长是＿＿＿
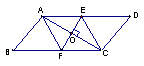[例4] 已知：如图，平行四边形ABCD的对角线AC的垂直平分线与边AD、BC分别相交于点E、F.
求证：四边形AFCE是菱形.
3. 正方形的性质和判定
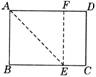
[例5]如图，一张矩形纸片，要折叠出一个最大的正方形，小明把矩形的一个角沿折痕AE翻折上去，使AB和AD边上的AF重合，则四边形ABEF就是一个最大的正方形，他的判断方法是＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿。
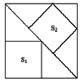[例6如图，大正方形中有2个小正方形，如果它们的面积分别是 S1、S2 ，那么S1、S2的大小关系是（ ）
A、S1 > S2 B、S1 = S2
C、S1<S2 D、S1、S2 的大小关系不确定
4. 中位线的应用
[例7]如图，正方形ABCD的周长为16cm，顺次连接正方形ABCD各边的中点，得到四边形EFGH，则四边形EFGH的周长等于 cm，四边形EFGH的面积等于 cm2.
〖考题训练〗
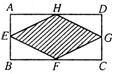1．已知：如图，在矩形ABCD中，E、F、G、H分别为边AB、BC、CD、DA的中点，若AB＝2，AD＝4，则图中阴影部分的面积为（ ）
A、3 B、4 C、6 D、8
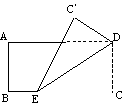2．将一张矩形纸片ABCD如图那样折起，使顶点C落在C¢处，其中AB＝4，若ÐC¢ED＝30º，则折痕ED的长为（
）
A、4 B、4 C、8 D、5
3．如图，E、F、G、H分别是四边形ABCD四条边的中点，要使四边形EFGH为矩形，四边形ABCD应具备的条件是（ ）.
A、一组对边平行而另一组对边不平行
B、对角线相等
C、对角线互相垂直 D、对角线互相平分
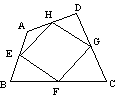4．如图，在四边形ABCD中，E、F、G、H分别是边AB、BC、CD、DA的中点，请添加一个条件，使四边形EFGH为菱形，并说明理由．
解：添加的条件：
理由：
5．如图，菱形ABCD中，AB＝4，E为BC中点，AE^BC，AF^CD于点F，CG∥AE，CG交AF于点H，交AD于点G。
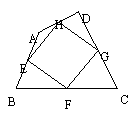（1）求菱形ABCD的面积；
（2）求ÐCHA的度数。
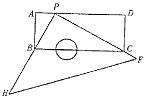6．如图，有一块塑料矩形模板ABCD，长为10cm，宽为4cm，将你手中足够大的直角三角板 PHF 的直角顶点P落在AD边上（不与A、D重合），在AD上适当移动三角板顶点P：
①能否使你的三角板两直角边分别通过点B与点C？若能，请你求出这时 AP 的长；若不能，请说明理由.
②再次移动三角板位置，使三角板顶点P在AD上移动，直角边PH 始终通过点B，另一直角边PF与DC的延长线交于点Q，与BC交于点E，能否使CE=2cm？若能，请你求出这时AP的长；若不能，请你说明理由.
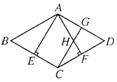
7．已知：在△ABC中，AB=AC=a，M为底边BC上任意一点，过点M分别作AB、AC的平行线交AC于P，交AB于Q.
(1)求四边形AQMP的周长；
(2)写出图中的两对相似三角形（不需证明）；
(3)M位于BC的什么位置时，四边形AQMP为菱形？说明你的理由.
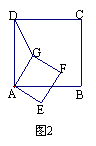
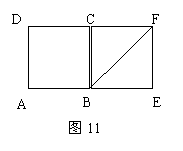
8．如图1，正方形ABCD和正方形BEFC。
操作：M是线段AB上一动点，从A点至B点移动，DM⊥MN，交对角线BF于点N。
探究：线段DM和MN之间的关系，并加以证明。
说明：如果你经历反复探索，没有找到解决问题的方法，请你把探索过程中的某种思路过程写出来（要求至少写3步）；（2）在你经历说明（1）的过程之后，可以从下列①、②中选取一个补充或更换已知条件，完成你的证明。注意：选取①完成证明得9分；选取②完成证明得6分。①M是线段AB的中点；②M、N分别是线段AB、BF的中点。
附加题
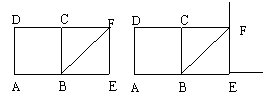
如图2，当M是线段AE延长线上一动点，DM⊥MN，交对角线BF延长线于点N，探究线段DM和MN之间的关系，并加以证明。
〖课后作业〗
（19）矩形、菱形、正方形
1．如图，EF过矩形ABCD对角线的交点O，且分别交AB、CD于E、F，那么阴影部分的面积是矩形ABCD的面积的……………（ ）
A、
B、
C、
D、
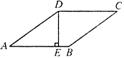2．请你添加一个条件，使□ABCD成为一个菱形，你添加的条件是＿＿＿＿＿＿＿。
3．用两个全等的三角形最多能拼成＿＿＿＿个不同的平行四边形。
4．下列命题正确的是（ ）
A、用正六边形能镶嵌成一个平面
B、有一组对边平行的四边形是平行四边形
C、正五角星是中心对称图形
D、对角线互相垂直的四边形是菱形
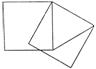5．如图，有两个正方形和一个等边三角形，则图中度数30º的角有（ ）
A、1个 B、2个 C、3个 D、4个
6．若四边形的两条对角线相等，则顺次连结该四边形各边中点所得的四边形是（ ）
A、梯形 B、矩形 C、菱形 D、正方形
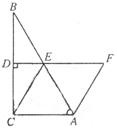
7．如图，在Rt△ABC中，ÐACB＝90º，ÐBAC＝60º，DE垂直平分BC，垂足为D交AB于点E。又点F在DE的延长线上，且AF＝CE。求证：四边形ACEF是菱形。
8．已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.
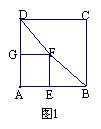(1) 如图1, 连结DF、BF,若将正方形AEFG绕点A按顺时针方向旋转,判断命题:“在旋转的过程中线段DF与BF的长始终相等.”是否正确,若正确请证明,若不正确请举反例说明;
(2) 若将正方形AEFG绕点A按顺时针方向旋转, 连结DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长始终相等.并以图2为例说明理由.
