中考数学模拟试题45
一、填空题:（每题3分，共30分）
1．据中新社报道：2010年我国粮食产量将达到千克，用科学记数法表示这个粮食产量为____
__千克；毛
2．分解因式：
；
3．如图，∠1＝∠2，要判断AB∥DF，需要增加条件 ；
4．抛物线
的对称轴是_____ _；
5．如图2，菱形ABCD的对角线的长分别为2和5，P是对角线AC上任一点（点P不与点A、C重合），且PE∥BC交AB于E，PF∥CD交AD于F，则阴影部分的面积是_____ _；
6．某地连续九天的最高气温统计如下表：
| 最高气温（℃） | 22 | 23 | 24 | 25 |
| 天 数 | 1 | 2 | 2 | 4 |
则这组数据的中位数与众数分别 ；
7．已知⊙O1的半径是3，⊙O2的半径是4，O1O2=8，则这两圆的位置关系是 ；
8．一组数据如下10，10，8，
,已知这组数据的众数与平均数相等，则这组数据的中位数
为
9.正
边形的每个外角都是
，那么这个正边形的边数
；
10．用相同长度的火柴棒摆成如图连在一起的正方形，摆个，要多少根火柴？你认真分析，写理由以及结果（用的式子表示结果）
结果__________________.
二、选择题（以下每小题均有A、B、C、D四个选项，其中只有一个选项正确，请把正确选项的字母选入该题括号内.每小题4分，共24分）
11．下面抽样调查中，选取的样本合适的是 （ ）
（A） 为了了解同学们主要有哪些兴趣爱好，小明利用课外活动时间到学校操场随机采访了8名同学
（B） 为了了解某校全体同学的视力情况，小华调查了自己班上的45名同学
（C） 为了了解一批冰箱的冷冻效果，从中随机抽取了50台进行试验
（D） 为了了解同学们用于做数学作业的时间，某同学在网上做了调查。
12．给出下面四个命题：(1)一组对边平行的四边形是梯形;(2)一条对角线平分一个内角的平行四边形是菱形;(3)两条对角线互相垂直的矩形是正方形;(4)一组对边平行,另一组对边相等的四边形是平行四边形,其中真命题的个数有 （ ）
（A）1个 （B）2个 （C）3个 （D）4个
13．如图，一张长方形纸沿AB对折，以AB中点O为顶点将平角五等分，并沿五等分的折线折叠，再沿CD剪开，使展开后为正五角星（正五边形对角线所构成的图形）.则∠OCD等于 （ ）
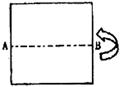
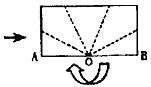
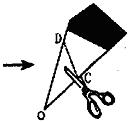
A． 108° B． 144° C． 126° D． 129°
14．关于
的方程
有实数根，则
的取值范围是 （ ）
（A） 
（B） ≥－4 （C）
≥－4且≠0 （D）≤－4
15．对某班60名学生参加毕业考试成绩
（成绩均为整数）整理后，画出频率
分布直方图，如图所示，则该班学生
及格人数为（ ）
A.45 B.51 C.54 D.57
16．如果用□表示1个立方体，用
表示两个立方体叠加，用■表示三个立方体叠加，那么下面右图由7个立方体叠成的几何体，从正前方观察，可画出的平面图形是 （ ）
 |
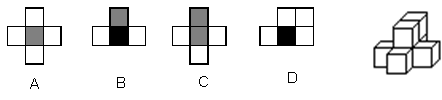三．解答题：
17．（本题满分8分）化简求值：
，其中
；
18.（本题满分10分）
下面两幅统计图（如图8、图9），反映了某市甲、乙两所中学学生参加课外活动的情况.请你通过图中信息回答下面的问题.
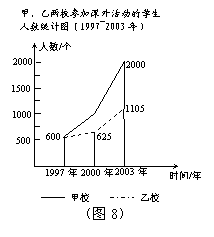
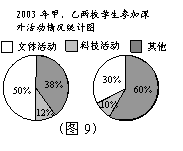
（1）通过对图8的分析，写出一条你认为正确的结论；（3分）
（2）通过对图9的分析，写出一条你认为正确的结论；（3分）
（3）2003年甲、乙两所中学参加科技活动的学生人数共有多少？（4分）
19.（本题满分12分）
已知：反比例函数
和一次函数
，其中一次函数的图像经过点
，
，
（1） 试求反比例函数的解析式；
（2） 若点A在第一象限，且同时在上述两函数的图像上，求A点的坐标。
20.（本题满分9分）
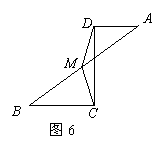
如图5，梯形ABCD中，AD//BC，AD⊥DC，M为AB的中点。
（1）求证：MD=MC；
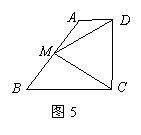
（2）平移AB使AB与CD相交，且保持AD//BC与 AD⊥DC，M仍为AB的中点（如图6），试问（1）的结论是否仍然成立？请证明你的结论。
21.（本题满分9分）
今年，我国政府为减轻农民负担，决定在5年内免去农业税.某乡今年人均上缴农业税25元，若两年后人均上缴农业税为16元，假设这两年降低的百分率相同.
（1）求降低的百分率；
（2）若小红家有4人，明年小红家减少多少农业税？
（3）小红所在的乡约有16000农民，问该乡农民明年减少多少农业税.
22.（本题满分9分）
某校准备在甲、乙两家公司为毕业班学生制作一批纪念册．甲公司提出：每册收材料费5元，另收设计费1500元；乙公司提出：每册收材料费8元，不收设计费．
（1）请写出制作纪念册的册数x与甲公司的收费
（元）的函数关系式；
（2）请写出制作纪念册的册数x与乙公司的收费
（元）的函数关系式；
（3）如果学校派你去甲、乙两家公司订做纪念册，你会选择哪家公司?
23.（本题满分7分）
已知：如图，△ABC中，AB=AC，矩形BCDE的边DE分别与AB、AC交于点F、G．
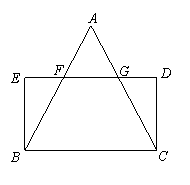求证：EF=DG.
24.（本题满分9分）
下图为住宅区内的两幢楼，它们的高
，现需了解甲楼对乙楼的采光的影响情况。当太阳光与水平线的夹角为30°时。试求：
(1）若两楼间的距离
时，甲楼的影子，落在乙楼上有多高？
(2）若甲楼的影子，刚好不影响乙楼，那么两楼的距离应当有多远？
25.（本题满分12分）
图1是棱长为a的小正方体，图2、图3由这样的小正方体摆放而成．按照这样的方法继续摆放，由上而下分别叫第一层、第二层、…、第n层，第n层的小正方体的个数为s．解答下列问题：
 |
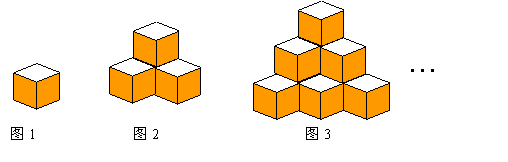（1）按照要求填表：
| n | 1 | 2 | 3 | 4 | … |
| |||||
| s | 1 | 3 | 6 | … |
| ||||||
| n | 1 | 2 | 3 | 4 | … |
| |||||
| s | 1 | 3 | 6 | … |
| ||||||
| n | 1 | 2 | 3 | 4 | … |
| |||||
| s | 1 | 3 | 6 | … |
| ||||||
| n | 1 | 2 | 3 | 4 | … | ||||||
| s | 1 | 3 | 6 | … | |||||||
| n | 1 | 2 | 3 | 4 | … |
| s | 1 | 3 | 6 | … |
| n | 1 | 2 | 3 | 4 | … |
| s | 1 | 3 | 6 | … |
（2）写出当n=10时，s = ．
（3）根据上表中的数据，把s作为纵坐标，n作为横坐标，在平面直角坐标系中描出相应的各点．
（4）请你猜一猜上述各点会在某一函数图象上吗？如果在某一函数图象上，求出该函数的解析式；如果不在某一函数图象上，说明理由．
26.（本题满分11分）
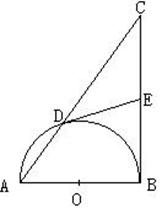
如图，以Rt△ABC的直角边AB为直径的半圆O，与斜边AC交于D，E是BC边上的中点，连结DE.
(1) DE与半圆O相切吗？若相切，请给出证明；若不相切，请说明理由；
(2)
若AD、AB的长是方程
的两个根，求直角边BC的长。
参考答案:
一． 填空题：
1．
； 2．
； 3．
； 4．
；
5．
； 6．
，
； 7．外离； 8．
； 9．
； 10．
；
二．选择题：
11．C； 12．B； 13．C； 14．C； 15．C； 16．B；
三．解答题：
17．原式
当时，
原式
18．（1）1997年至2003年甲校学生参加课外活动的人数比乙校增长的快 ；
（学生给出其它答案，只要正确、合理均给3分）
（2）甲校学生参加文体活动的人数比参加科技活动的人数多；
（学生给出其它答案，只要正确、合理均给3分）
（3）
答：2003年两所中学的学生参加科技活动的总人数是1423人
19．解：（1） 因为一次函数的图像经过点（
,
）
所以有 
解得 
所以反比例函数的解析式为
（2）由题意得：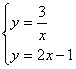
解这个方程组得：
因为点A在第一象限，则
，
，
所以点A的坐标为（
，2）
20．（1）证明：取DC的中点N
∵M是AB的中点 AD//BC ∴MN//AD
∵AD⊥DC ∴MN⊥DC
∴MN为DC的垂直平分线
∴MD=MC
（2）结论仍然成立
证明：过M作MN⊥DC于N
∵AD⊥DC AD//BC ∴MN//AD//BC ∴AM ：BM = DN ：NC
∵AM=BM ∴DN=NC
∴MN为DC的垂直平分线
∴MD=MC。
21．（1）设降低的百分率为x，
依题意有 解得x1＝0.2＝20％，x2 ＝1.8(舍去)
（2）小红全家少上缴税 25×20％×4＝20（元）
（3）全乡少上缴税 16000×25×20％＝80000（元）
答略
22． 27．（1）解：由题意得：
．
（2）解：由题意得：
．
（3）解：∵ 当
时，
，
．
当
时，
，
．
当
时，
，
．
∴ 当订做纪念册的册数为500时，选择甲、乙两家公司均可．
当订做纪念册的册数少于500时，选择乙公司．
当订做纪念册的册数多于500时，选择甲公司．
23．证明：∵AB=AC
∴∠ABC=∠ACB
又∵四边形BCDE是矩形
∴BE=DC，∠E=∠D=∠EBC=∠BCD=90°
∴ ∠EBF=∠DCG
∴△BEF≌△CDG
∴EF=DG
24．（1）如图，太阳光交CD于G交AC的延长线
于F，过G作AC的平行线GE交AB于E；
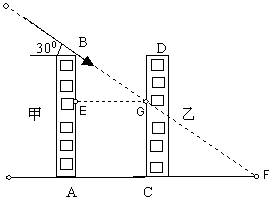在Rt⊿BGE中，EG = AC = 24米，∠BGE =
∴BE =
米
∴
（米）
∴甲楼的影子，落在乙楼上有
米。
（2）在Rt⊿ABF中，AB = 30米，∠F =，
∴
（米）
∴若甲楼的影子，刚好不影响乙楼，那么两楼的距离应当至少相距
米远。
25． （1）10
（2）55
（3）略…
（4）经观察所描各点，它们在二次函数的图象上。
设：此函数的解析式为
由题意得：
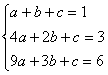解得：
所以此函数的解析式为
26．解：（1）DE与半圆O相切.
证明： 连结OD、BD
∵AB是半圆O的直径
∴∠BDA=∠BDC=90°
∵在Rt△BDC中,E是BC边上的中点
∴DE=BE
∴∠EBD＝∠BDE
∵OB=OD
∴∠OBD=∠ODB
又∵∠ABC＝∠OBD+∠EBD＝90°
∴∠ODB+∠EBD=90°
∴DE与半圆O相切.
（2）解：∵在Rt△ABC中，BD⊥AC
∴ Rt△ABD∽Rt△ABC
∴ = 即AB2=AD·AC
∴ AC=
∵ AD、AB的长是方程的两个根
∴ 解方程得： 
，
；
∵ AD<AB
∴ AD = 4 AB = 6
∴ AC = 9
在Rt△ABC中，AB = 6 ，AC = 9
∴ 
.毛