初中数学总复习（31）统计1
〖考试内容〗
数据，数据的收集、整理、描述和分析.
抽样，总体，个体，样本.
加权平均数.数据的集中程度与离散程度.极差和方差.
样本估计总体.样本的平均数、方差，总体的平均数、方差.
统计与决策，数据信息，统计在社会生活及科学领域中的应用.
〖考试要求〗
①会收集、整理、描述和分析数据，能用计算器处理较为复杂的统计数据.
②了解抽样的必要性，能指出总体、个体、样本.知道不同的抽样可能得到不同的结果.
③理解并会计算加权平均数，能根据具体问题，选择合适的统计量表示数据的集中程度.
④会探索如何表示一组数据的离散程度，会计算极差与方差，并会用它们表示数据的离散程度.
⑤体会用样本估计总体的思想，能用样本的平均数、方差来估计总体的平均数和方差.
⑥能根据统计结果做出合理的判断和预测，体会统计对决策的作用，能比较清晰的表达自己的观点，并进行交流.
〖考点复习〗
1．普查与抽样调查
[例1]下列调查，比较容易用普查方式的是（ ）
A、了解贵阳市居民年人均收入
B、了解贵阳市初中生体育中考的成绩
C、了解贵阳市中小学生的近视率
D、了解某一天离开贵阳市的人口流量
2．平均数、中位数、众数
[例2]甲、乙两名运动员在6次百米跑训练中的成绩如下. （单位：秒）
| 甲 | 10.8 | 10.9 | 11.0 | 10.7 | 11.2 | 10.8 |
| 乙 | 10.9 | 10.9 | 10.8 | 10.8 | 10.5 | 10.9 |
请你比较这两组数据的众数、平均数、中位数，谈谈你的看法.
3．极差、方差
[例3]下表给出了苏州市2005年5月28日至6月3日的最高气温，则这些最高气温的极差是 ℃。
| 日期 | 5月28日 | 5月29日 | 5月30日 | 5月31日 | 6月1日 | 6月2日 | 6月3日 |
| 最高气温 | 26℃ | 27℃ | 30℃ | 28℃ | 27℃ | 29℃ | 33℃ |
[例4]（2005徐州）小明和小兵参加某体育项目训练，近期的8次测试成绩(分)如下表：
| 测试 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | 第7次 | 第8次 |
| 小明 | 10 | 10 | 11 | 10 | 16 | 14 | 16 | 17 |
| 小兵 | 11 | 13 | 13 | 12 | 14 | 13 | 15 | 13 |
(1)根据上表中提供的数据填写下表：
| 平均数(分) | 众数(分) | 中位数(分) | 方差 | |
| 小明 | 10 | 8.25 | ||
| 小兵 | 13 | 13 |
(2)若从中选一人参加市中学生运动会，你认为选谁去合适呢？请说明理由.
4．数据的选择和应用
[例5]为筹备班级的初中毕业联欢会，班长对全班学生爱吃哪几种水果作了民意调查．那么最终买什么水果，下面的调查数据中最值得关注的是（ ）
A．中位数 B．平均数
C．众数 D．加权平均数
[例6] 在某旅游景区上山的一条小路上，有一些断断续续的台阶.下图是其中的甲、乙段台阶路的示意图.
请你用所学过的有关统计知识（平均数、中位数、方差和极差）回答下列问题：
（1）两段台阶路有哪些相同点和不同点？
（2）哪段台阶路走起来更舒服？为什么？
（3）为方便游客行走，需要重新整修上山的小路.对于这两段台阶路，在台阶数不娈的情况下，请你提出合理的整修建议.
 |
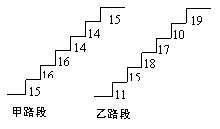上图中的数字表示每一级台阶的高度(单位:cm).并且数15,16,16,14,14,15的方差
,数据11,15,18, 17,10,19的方差
〖考题训练〗
1．某市社会调查队对城区内一个社区居民的家庭经济状况进行调查. 调查的结果是, 该社区工有500户, 高收入、中等收入和低收入家庭分别有125户、280户和95户。 已知该市有100万户家庭下列表示正确的是 ( )
A. 该市高收入家庭约25万户
B. 该市中等收入家庭约56万户
C. 该市低收入家庭业19万户
D. 因城市社区家庭经济状况好,所以不能据此估计全市所有家庭经济状况
2．某住宅小区6月份随机抽查了该小区6天的用水量（单位：吨），结果分别是30、34、32、37、28、31，那么，请你估计该小区6月份（30天）的总用水量约是 吨.
3．一组数据3、8、8、19、19、19、19的众数是_______。
4已知一组数据5，15，75，45，25，75，45，35，45，35，那么40时这一组数据的（ ）
A．平均数但不是中位数
B.平均数也是中位数
C．众数 D. 中位数但不是平均数
5．期中考试后，学习小组长算出全组 5位同学数学成绩的平均分为M，如果把M当成另一个同学的分数，与原来的5个分数一起，算出这6个分数的平均值为N，那么M：N为（ ）
A 5:6 B 1 C 6:5 D 2
| 去皮前各菠萝的质量 | 1.0 | 1.1 | 1.4 | 1.2 | 1.3 |
| 去皮后各菠萝的质量 | 0.6 | 0.7 | 0.9 | 0.8 | 0.9 |
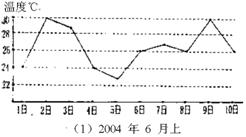
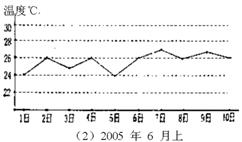
6．图（1）（2）是根据某地近两年6月上旬日平均气温情况绘制的折线统计图，通过观察图表，可以判断这两年6月上旬气温比较稳定的年份是__________。
7．对甲、乙两台机床生产的零件进行抽样测量，其平均数、方差计算结果如下：
机床甲：
=10，
=0.02；机床乙：
=10，
=0.06，由此可知：________（填甲或乙）机床性能好.
8．甲、乙、丙三台包装机同时分装质量为400克的茶叶.从它们各自分装的茶叶中分别随机抽取了10盒，测得它们的实际质量的方差如下表所示：
| 甲包装机 | 乙包装机 | 丙包装机 | |
| 方差（克2） | 31．96 | 7．96 | 16．32 |
根据表中数据，可以认为三台包装机中, _______包装机包装的茶叶质量最稳定.
9．甲、乙两班各有51名同学，一次数学考试成绩甲、乙两班的中位数分别是66分、79分，若不少于79分算优秀，则甲、乙两班优秀率高的班级是_____________。
10．某水果店有200个菠萝，原计划以2.6元/千克的价格出售，现在为了满足市场需要，水果店决定将所有的菠萝去皮后出售。以下是随机抽取的5个菠萝去皮前后相应的质量统计表：（单位：千克）
（1）计算所抽取的5个菠萝去皮前的平均质量和去皮后的平均质量，并估计这200个菠萝去皮前的总质量和去皮后的总质量。
（2）根据（1）的结果，要使去皮后这200个菠萝的销售总额与原计划的销售总额相同，那么去皮后的菠萝的售价应是每千克多少元？
11．某地连续九天的最高气温统计如下表：
| 最高气温（℃） | 22 | 23 | 24 | 25 |
| 天数 | 1 | 2 | 2 | 4 |
则这组数据的中位数与众数分别是（ ）
A、24、25 B、24.5、25
C、25、24 D、23.5、24
12．某校要从小王和小李两名同学中挑选一人参加全国数学竞赛，在最近的五次选拔测试中，他俩的成绩分别如下表：
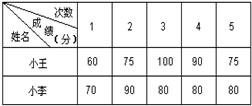
根据上表解答下列问题：
（1）完成下表：
| 姓名 | 极差 (分) | 平均成 绩(分) | 中位数 (分) | 众数 (分) | 方差 |
| 小王 | 40 | 80 | 75 | 75 | 190 |
| 小李 |
（2）在这五次测试中，成绩比较稳定的同学是谁？若将80分以上（含80分）的成绩视为优秀，则小王、小李在这五次测试中的优秀率各是多少？（3分）
（3）历届比赛表明，成绩达到80分以上（含80分）就很可能获奖，成绩达到90分以上（含90分）就很可能获得一等奖，那么你认为应选谁参加比赛比较合适？说明你的理由（2分）
①．下列调查中，适合用普查方法的是（ ）
A、电视机厂要了解一批显象管的使用寿命
B、要了解我市居民的环保意识
C、要了解我市“阳山水蜜桃”的甜度和含水量
D、要了解你校数学教师的年龄状况
②．为发展农业经济，致富奔小康，养鸡专业户王大伯2004年养了2000只鸡，上市前，他随机抽取了10只鸡，称得重量统计如下表：
| 重量（单位：kg） | 2 | 2.2 | 2.5 | 2.8 | 3 |
| 数量（单位：只） | 1 | 2 | 4 | 2 | 1 |
估计这批鸡的总重量为 kg.
③数据“1，2，1，3，1”的众数是 ( ).
A.1 B.1.5 C.1.6 D.3
④．六个学生进行投篮比赛，投进的个数分别为2、3、3、5、10、13，这六个数的中位数为 （ ）
A、3 B、4 C、5 D、6
⑤．某青年排球队12名队员的年龄情况如下：
| 年龄（单位：岁） | 18 | 19 | 20 | 21 | 22 |
| 人 数 | 1 | 4 | 3 | 2 | 2 |
则这个队队员年龄的众数和中位数是（ ）
A、19，20 B、19，19
C、19，20.5 D、20，19
⑥．小明五次测试成绩如下:91、89、88、90、92，则这五次测试成绩的平均数是 ，方差是 。
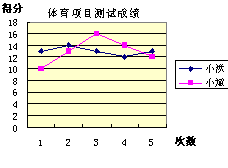⑦．小洪和小斌两人参加体育项目训练，近期的5次测试成绩如图所示，根据分析，你认为他们中成绩较为稳定的是
．
⑧．某服装销售商在进行市场占有率的调查时，他最应该关注的是（ ）
A. 服装型号的平均数
B. 服装型号的众数
C. 服装型号的中位数
D. 最小的服装型号
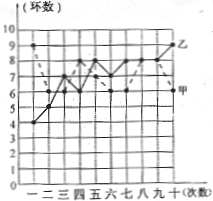
⑨．射击集训队在一个月的集训中，对甲、乙两名运动员进行了10次测试，成绩如图所示：
（1）根据右图所提供的信息填写下表：
| 平均数 | 众数 | 方差 | |
| 甲 | 7 | 1.2 | |
| 乙 | 2.2 |
（2）如果你是教练，会选择哪位运动员参加比赛？请说明理由。
 |
⑩.为了从甲、乙两名学生中选拔一人参加今年六月份的全县中学生数学竞赛，每个月对他们的学习水平进行一次测验，下图是两人赛前5次测验成绩的折线统计图.
(1)别求出甲、乙两名学生 5次测验成绩的平均数及方差.
(2)如果你是他们的辅导教师，应选派哪一名学生参加这次数学竞赛.请结合所学统计知识说明理由.
