初中数学图形的轴对称平移旋转

（25）图形的轴对称、图形的平移、图形的旋转

〖考试内容〗

图形的轴对称、平移、旋转.

〖考试要求〗

①通过具体实例认识轴对称（或平移、旋转），探索它们的基本性质.

②能够按要求作出简单平面图形经过轴对称（或平移、旋转）后的图形，能作出简单平面图形经过一次或两次轴对称后的图形.

③探索基本图形（等腰三角形、矩形、菱形、等腰梯形、正多边形、圆）的轴对称性质及其相关性质.了解平行四边形、圆是中心对称图形.

④探索图形之间的变换关系（轴对称、平移、旋转及其组合）.利用轴对称（或平移、旋转）及其组合进行图案设计；认识和欣赏轴对称（或平移、旋转）在现实生活中的应用.

〖考点复习〗

[例1]

[例1]．下列图形中只能用其中一部分平移可以得到的是　　 （　　　）

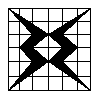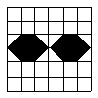A　　　　　　　　　 B　　　　　　　　　　

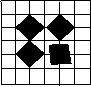C　　　　　　　　　 D

[例2]．下列图形中，既是轴对称图形又是中心对称图形的是（　 ）　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

 A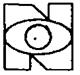． 　　B．　　　　　　

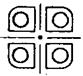C．　　　　 D．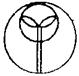

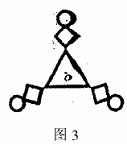
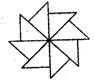[例3]．右图可以看作是一个等腰直角三角形旋转若干次而生

成的则每次旋转的度数可以

是（　　）。

A．90⁰B．60⁰ 

C．45⁰D．30⁰

〖考题训练〗

1．在5×5方格纸中将图（1）中的图形N平移后的位置如图（2）中所示，那么正确的平移方法是（　　）.

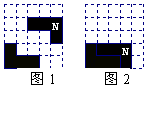(A)先向下移动1格，再向左移动1格

(B)先向下移动1格，再向左移动2格

(C)先向下移动2格，再向左移动1格

(D)先向下移动2格，再向左移动2格

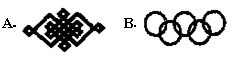2．下列轴对称图形中（如图2），只有两条对称轴的图形是（　　）

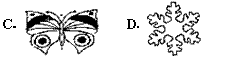
3．下面给出的是一些产品的图案，从几何图形的角度看，这些图案既是中心对称图形又是轴对称图形的是（　　 ）

　

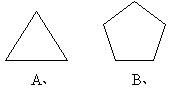
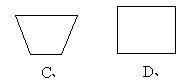
4．下列图形中，既是轴对称图形，又是中心对称图形的是 (　　　)

5．小亮在镜中看到身后墙上的时钟如下, 你认为实际时间最接近8:00的是 (　　)

　　

A. 　　　　　　　　　　　　B.

　　

C. 　　　　　　　　　 　　　D.

6．下面有4个汽车标致图案，其中是轴对称图形的是

①　　　　　　　　　　 ②　

③　　　　　　　　　　 ④

A、②③④　　　　B、①③④　　　

　C、①②④　　　　D、①②③

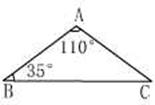
7．图3是两张全等的图案，它们完全重合地叠放在一起，按住下面的图案不动，将上面图案绕点O顺时针旋转，至少旋转度角后，两张图案构成的图形是中心对称图形.

8．在平面内，如果一个图形绕一个定点旋转一定的角度后能与自身重合，那么就称这个图形是旋转对称图形，转动的这个角称为这个图形的一个旋转角。例如：正方形绕着它的对角线的交点旋转90°后能与自身重合（如图），所以正方形是旋转对称图形，它有一个旋转角为90°。

（1）判断下列命题的真假（在相应的括号内填上“真”或“假”）。

①等腰梯形是旋转对称图形，它有一个旋转角为180°。（　　　　 ）

② 矩形是旋转对称图形，它有一个旋转角为180º（　 　　）

　（2）填空：下列图形中，是旋转对称图形，且有一个旋转角为120°的是　　　　　　 （写出所有正确结论的序号）：

①正三角形；②正方形；③正六边形；④正八边形 。　　

（3）写出两个多边形，它们都是旋转对图形，都有一个旋转角为72°，并且分别满足下列条件①是轴对称图形，但不是中心对称图形：　　　　　　　　  　　 

②既是轴对称图形，又是中心对称图形：　　　　　　　　  　 

9图(1)是一个10×10格点正方形组成的网格. △ABC是格点三角形(顶点在网格交点处), 请你完成下面两个问题:

(1) 在图(1)中画出与△ABC相似的格点△A₁B₁C₁和△A₂B₂C₂, 且△A₁B₁C₁与△ABC的相似比是2, △A₂B₂C₂与△ABC的相似比是.

(2) 在图(2)中用与△ABC、△A₁B₁C₁、△A₂B₂C₂全等的格点三角形(每个三角形至少使用一次), 拼出一个你熟悉的图案,并为你设计的图案配一句贴切的解说词.

10．如图，在△ABC中，∠A=110°，∠B=35°，请你应用变换的方法得到一个三角形使它与△ABC全等，且要求得到的三角形与原△ABC组成一个四边形。

(1)　　 要求用两种变换方法解决上述问题；（写出变换名称，画出图形即可）

(2)　　 指出四边形是什么图形？（不要求证明）

说明：如用两种平移变换方法解决此题算一种变换；两种变换是指平移，旋转等不同变换。

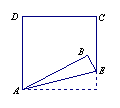
11．如图，将正方形ABCD的一角折叠，折痕为AE，比大.设和的度数分别为,，那么,所适合的一个方程组是（　  ）

（A）　　 （B）　

（C）　 （D）

〖课后作业〗

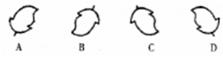
①．观察下面图案，在 A、B、C、D 四幅图案中，能通过图案（1）的平移得到的是（　　）

②、所列图形中是中心对称图形的为（　 ）

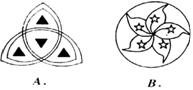
③．下列图形中，是中心对称图形，但不是轴对称图形的是（　　）.

A、正方形 B、矩形 C、菱形 D、平行四边形

④．图6是我国古代数学赵爽所著的《勾股圆方图注》中所画的图形，它是由四个相同的直角三角形拼成的，下面关于此图形的说法正确的是(　　 )

A．它是轴对称图形，但不是中心对称图形

B．它是中心对称图形，但不是轴对称图形

C．它既是轴对称图形，又是中心对称图形

D．它既不是轴对称图形，又不是中心对称图形

⑤．绕一定点旋转180°后与原来图形重合的图形是中心对称图形，正六边形就是这样的图形．小明发现将正六边形绕着它的中心旋转一个小于180°的角，也可以使它与原来的正六边形重合，请你写出小明发现的一个旋转角的度数：_____________________

⑥从下面两题中任选一题进行解答（（1）题6分，（2）题8分）

（1）先在左面的一块方格纸上画一个轴对称图形作为基础图形，再将基础图形去掉或添上一部分，使新图形仍为轴对称图形，画在右面的方格纸上。

（2）先在左面的一块方格纸上画一个轴对称图形作为基础图形，再将基础图形的一部分平移或旋转到剩余图形的某一位置组成新的图形，使新图形仍为轴对称图形，画在右面的方格纸上。

⑦．将一圆形纸片对折后再对折，得到图，然后沿着图中的虚线剪开，得到两部分，其中一部分展开后的平面图形是(　　)