（17）三角形
〖考试内容〗
三角形，三角形的角平分线、中线和高.三角形中位线.全等三角形，三角形全等的条件.等腰三角形的条件及性质，等边三角形的性质，直角三角形的条件及性质.勾股定理，勾股定理的逆定理.
〖考试要求〗
①了解三角形有关概念（内角、外角、中线、高、角平分线），会画出任意三角形的角平分线、中线和高，了解三角形的稳定性.
②掌握三角形中位线的性质.
③了解全等三角形的概念，掌握两个三角形全等的条件.
④了解等腰三角形、等边三角形、直角三角形的有关概念，掌握等腰三角形、等边三角形、直角三角形的性质，掌握一个三角形是等腰三角形、直角三角形的条件.
⑤掌握勾股定理，会运用勾股定理解决简单问题；会用勾股定理的逆定理判定直角三角形.
〖考点复习〗
1．三角形的内角和定理及推论
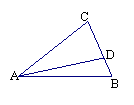
[例1] 已知：如图,
D是BC上一点, ∠C＝62°,
∠CAD＝32°,则 ∠ADB＝ 度.
2．三角形三边关系
[例2]以下列各组线段长为边，能构成三角形的是（ ）
A、4cm、5cm、6cm B、2cm、3cm、5cm
C、4cm、4cm、9cm D、12cm、5cm、6cm
3．全等三角形
[例3] 如图，已知△ABC的六个元素,则下面甲、乙、丙三个三角形中和△ABC全等的图形是（ ）
|
[例4] 如图，若△ABC≌△DEF，则∠E等于（ ）
A．30° B． 50° C．60° D．100°
 |
[例5]已知：如图，点C、D在线段AB上，PC＝PD。
请你添加一个条件，使图中存在全等三角形并给予证明。
所加条件为＿＿＿＿＿，你得到的一对全等三角形是△＿＿＿≌△＿＿＿。
4．等腰三角形
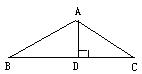
[例6] 如图，等腰三角形ABC的顶角为120º，腰长为10，则底边上的高AD＝＿＿＿＿。
5．直角三角形
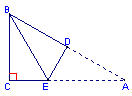[例7] 在三角形纸片ABC中，∠C＝90°，∠A＝30°，AC＝3，折叠该纸片，使点A与点B重合，折痕与AB、AC分别相交于点D和点E（如图2），折痕DE的长为
6．三角形中位线
[例8]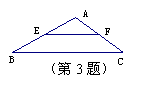 
如图所示，BC＝6，E、F分别是线段AB和线段AC的中点，那么线段EF的长是（ ）．
（A）6 （B）5 （C）4.5 （D）3
〖考题训练〗
 |
1．．如图，在锐角△ABC中，CD、BE分别是AB、AC边上的高，且CD、BE交于一点P，若ÐA＝50º，则ÐBPC的度数是（ ）
A、150º B、130º C、120º D、100º
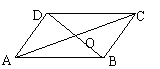2如图，□ABCD中，对角线AC和BD相交于点O，如果AC=12、BD=10、AB=m，那么m的取值范围是（ ）
A、1< m <11 B、2< m <22
C、10< m <12 D、5< m <6
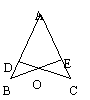
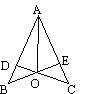3．如图，已知CD^AB，BE^AC，垂足分别为D、E，BE、CD交于点O，且AO平分ÐBAC，那么图中全等三角形共有＿＿＿对。
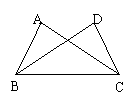
4．如图，已知，在△ABC和△DCB中，AC=DB，若不增加任何字母与辅助线，要使△ABC≌△DCB，则还需增加一个条件是__。
5．下列说法中，正确的是（ ）
A．两腰对应相等的两个等腰三角形全等
B．两锐角对应相等的两个直角三角形全等
C．两角及其夹边对应角相等的两个三角形全等
D．面积相等的两个三角形全等。
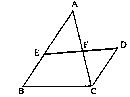6．如图，已知，在△ABC中，F是AC的中点，E为AB上一点，D为EF延长线上一点，∠A＝∠ACD
求证：CD∥AE
7．用一块等边三角形的硬纸片（如图1）做一个底面为等边三角形且高相等的无盖的盒子（边缝忽略不计，如图2），在△ABC的每个顶点处各剪掉一个四边形，其中四边形AMDN中，∠MDN的度数为（ ）
A. 100° B. 110°C. 120° D. 130°
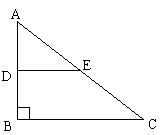
8．已知：如图（1），在Rt△ABC中，∠B=90°，D、E分别是边AB、AC的中点，DE=4，AC=10，则AB=_____________.
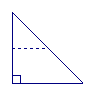
9．如图，将一张等腰直角三角形纸片沿中位线剪开，可以拼出不同形状的四边形，请写出其中两个不同的四边形的名称： 。
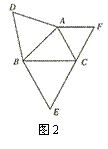
10．已知△ABC，分别以AB、BC、 CA为边向形外作等边三角形ABD、等边三角形BCE、等边三角形ACF.
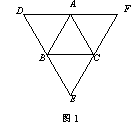
（1）如图1，当△ABC是等边三角形时，请你写出满足图中条件，四个成立的结论；
（2）如图2，当△ABC中只有∠ACB=60°时，请你证明S△ABC与S△ABD的和等于S△BCE与S△ACF的和.
 |
11．如图所示，一根长2a的木棍（AB），斜靠在与地面（OM）垂直的墙（ON）上，设木棍的中点为P. 若木棍A端沿墙下滑，且B端沿地面向右滑行.
（1）请判断木棍滑动的过程中，点P到点O的距离是否变化，并简述理由.
（2）在木棍滑动的过程中，当滑动到什么位置时，△AOB的面积最大？简述理由，并求出面积的最大值.
〖课后作业〗
1．在△ABC中，若ÐA＝78º36¢，ÐB＝57º24¢，则ÐC＝＿＿＿＿＿。
2．小芳要画一个有两边长分别为 5cm 和 6cm 的等腰三角形，则这个等腰三角形的周长是（ ）
A 16cm B 17cm C 16cm 或 17cm D 11cm
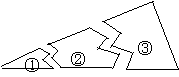3．如图,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块完全一样形状的玻璃.那么最省事的办法是带________去配. (
).
A.① B.② C.③ D.①和②
4．如图，AB＝AC，要使△ABE≌△ACD，应添加的条件是＿＿＿＿＿＿（添加一个条件即可）。
5．如果直角三角形的斜边与一条直角边的长分别是13cm和5cm，那么这个直角三角形的面积是 cm2．
6．如图，D、E、F分别为△ABC三边的中点，则与△DEF全等的三角形有（ ）
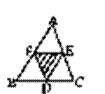A．1个 B．2个 C．3个 D．5个
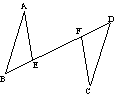
7．如图，AB∥CD，AB＝CD.点B、E、F、D在一条直线上，ÐA＝ÐC，求证：AE＝CF。
说明：证明过程中要写出每步的证明依据。
8．下面是数学课堂的一个学习片段, 阅读后, 请回答下面的问题:
学习等腰三角形有关内容后, 张老师请同学们交流讨论这样一个问题: “已知等腰三角形ABC的角A等于30°, 请你求出其余两角.”
同学们经片刻的思考与交流后, 李明同学举手说: “其余两角是30°和120°”; 王华同学说: “其余两角是75°和75°.” 还有一些同学也提出了不同的看法……
(1) 假如你也在课堂中, 你的意见如何? 为什么?
(2) 通过上面数学问题的讨论, 你有什么感受? (用一句话表示)