（10）不等式与不等式组
〖考试内容〗
不等式，不等式的基本性质，不等式的解集，一元一次不等式及其解法，
〖考试要求〗
①能够根据具体问题中的大小关系了解不等式的意义，掌握不等式的基本性质.
②会解简单的一元一次不等式，并能在数轴上表示出解集.会解由两个一元一次不等式组成的不等式组，并会用数轴确定解集.
〖考点复习〗
1. 不等式的基本性质
[例1若
，则下列各式中一定成立的是（ ）
A、
B、
C、
D、
2．不等式的解集
[例2]5. 不等式组
的解集为________。
[例3] 1.把不等式组
的解集表示在数轴上，正确的是（
）
 | |||
 | |||
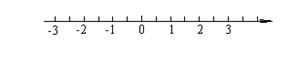（A） （B）
（C） （D）
3．一元一次不等式及其解法
[例4] 解不等式并把解集在数轴上表示出来：
≥
.
4．一元一次不等式组及其解法
[例5] 解不等式组 并把解集在数轴上表示出来。
〖考题训练〗
1．如果t>0,那么a+t与a的大小关系是 ( ).
A、a+t>a B、a+t<a C、a+t≥a D、不能确定
2．不等式组的解是( )
A、x≤2 B、x≥2 C、－1＜x≤2 D、x＞－1
3．关于x的不等式2x-a≤-1的解集如图所示，则a的取值是（）
A 0 B -3 C -2 D -1
4．不等式组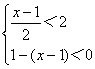
的解集是( )
A、2＜x＜5 B、0＜x＜5
C、2＜x＜3 D、x＜2
5．不等式组
的整数解是 。
6．解不等式组
7．．（本题满分6分）
解不等式组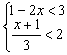
7．解不等式组 ，
并把解集在数轴上表示出来.
〖课后作业〗
1．据丽水气象台“天气预报”报道，今天的最低气温是17℃，最高气温是25℃，则今天气温t（℃）的范围是
A、t＜17 B、t＞25 C、t=21 D、17≤t≤25
2．如果关于x的不等式 (a+1) x>a+1的解集为x<1，那么a的取值范围是
A、 a>0 B、a<0 C、 a>-1 D、 a<-1
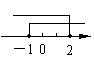
3．不等式组
的解集在数轴上表示正确的是
 |  |
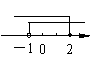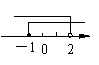A、
B、
 |
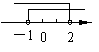C、 D、
4．不等式组
的解集在数轴上可表示为（ ）
A、 B、
C、 D、
5．解不等式组 并写
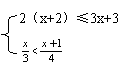
6．一个矩形，两边长分别为xcm和10cm，如果它的周长小于80cm，面积大于100cm2．求x的取值范围．