第三节 方程组
知识网络
一、
二、
典型例题
一、选择题
1.方程组
的一个解是（ ）
A.
B.
C.
D.
2.某校初三（2）班40名同学为“希望工程”捐款,共捐款100元.捐款情况如下表：
| 捐款（元） | 1 |
| 3 | 4 | ||
| 人 数 | 6 | 7 |
表格中捐款2元和3元的人数不小心被墨水污染已看不清楚.
若设捐款2元的有
名同学,捐款3元的有
名同学,根据题意,可得方程组
A、
B、
C、
D、
3.为了贫困家庭子女能完成初中学业，国家给他们免费提供教科书，
下表是某中学免费提供教科书补助的部分情况：
| 年级 项目 | 七 | 八 | 九 | 合计 |
| 每人免费补助金额(元) | 109 | 94 | 47.5 | ―― |
| 人数(人) | 40 | 120 | ||
| 免费补助总金额(元) | 1900 | 10095 |
若设获得免费提供教科书补助的七年级为x人，八年级为y人，根据题意列出方程组为( )
A．
B．
C．
D．
二、解答题
1．已知等式 (2A-7B) x+(3A-8B)=8x+10对一切实数x都成立，求A、B的值.
【解】 由题意有
解得：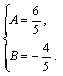
即A、B的值分别为
、
.
2为满足市民对优质教育的需求某中学决定改变办学条件计划拆除一部分旧校舍、建造新校舍。拆除旧校舍每平米需80元，建造新校舍每平米需700元。计划在年内拆除旧校舍与建造新校舍共7200平方米，在实施中为扩大绿化面积，新建校舍只完成了计划的80％，而拆除校舍则超过了10％，结果恰好完成了原计划的拆、除的总面积。
（1）求原计划拆建面积各多少平方米？
（2）若绿化1平方米需200元，那么在实际完成的拆、建工程中节余的资金用来绿化大约是多少平方米？
【解】设原计划拆除旧校舍x平方米，新建校舍y平方米，本世纪初题意得：
（1）
解得
（2）实际比原计划拆除与新建校舍节约资金是
（4800×80—2400×700）—〔4800×（1—10％）×80＋2400×80％×700〕
＝297600
用此资金可绿化面积是297600÷200＝1488（平方米）
答：原计划拆除旧戌舍4800平方米，新建校舍2400平方米，实际施工中节约的资金可绿化1488平方米
3.十堰市东方食品厂2003年的利润（总产值-总支出）为200万元，2004年总产值比2003年增加了20%，总支出减少了10%。2004年的利润为780万元。问2003年总产值、总支出各是多少万元？
【解】设2003年的总产值为x万元，则2004年的总产值为（1+20%）x万元，2003年的总支出为y万元，则2004年的总支出为（1－10%）y万元，则有：
∴
答：2003年的总产值为2000万元，总支出为1800万元
4．解方程组
【解】①＋②，得 3x＝15 ∴ x＝15
把x＝5代入①，得y＝2
∴
是原方程组的解
5．某商场购进甲、乙两种服装后，都加价40%标价出售。“春节”期间商场搞优惠促销，决定将甲、乙两种服装分别按标价的八折和九折出售。某顾客购买甲、乙两种服装共付款182元，两种服装标价之和为210元，问这两种服装的进价和标价各是多少元？
【解】设甲种服装的标价是x元，则进价是元；乙种服装的标价是y元，则进价是元。
依题意，得：
解之，得：
＝50(元)，＝100(元)
6．解方程：
【解】解：6－3(x＋1)=x2－1 x2＋3x－4=0 x＋4)(x－1)=0 x1=－4,x2=1
经检验x=1是增根，应舍去
∴原方程的解为x=－4
7．解方程组
【解】 
8．解方程组：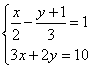
【解】
9.某水果批发市场香蕉的价格如下表：
| 购买香蕉数 (千克) | 不超过 20千克 | 20千克以上但不超过40千克 | 40千克以上 |
| 每千克价格 | 6元 | 5元 | 4元 |
张强两次共购买香蕉50千克(第二次多于第一次)，共付款264元，请问张强第一次、第二次分别购买香蕉多少千克?
【解】设张强第一次购买香蕉x千克，第二次购买香蕉y千克．由题意，得
0<x<25．
① 当0<x≤20，y≤40时，由题意，得
② 当0<x≤20，y>40时，由题意，得
(不合题意，舍去)．
③ 当20<x<25时，25<y<30．此时张强用去的款项为
5x+5y=5(x+y)=5×50=250<264(不合题意，舍去)
综合①②③可知，张强第一次购买香蕉14千克，第二次购买香蕉36千克.
10．某家庭装饰厨房需用480块某品牌的同一种规格的瓷砖，装饰材料商场出售的这种瓷砖有大、小两种包装，大包装每包50片，价格为30元；小包装每包30片，价格为20元，若大、小包装均不拆开零售，那么怎样制定购买方案才能使所付费用最少?
【解】根据题意，可有三种购买方案；
方案一：只买大包装，则需买包数为：
；
由于不拆包零卖．所以需买10包．所付费用为30×10=300(元)
方案二：只买小包装．则需买包数为：
所以需买1 6包，所付费用为1 6×20＝320(元)
方案三：既买大包装．又买小包装，并设买大包装
包．小包装
包．所需费用为W元。
则
∵
，且为正整数，
∴
9时，
290(元)．
∴购买9包大包装瓷砖和l包小包装瓷砖时，所付费用最少．为290元。
答：购买9包大包装瓷砖和l包小包装瓷砖时，所付费用最少为290元。
11.用8块相同的长方形地砖拼成一块矩形地面，地砖的拼放方式及相关数据如图所示，求每块地砖的长与宽。
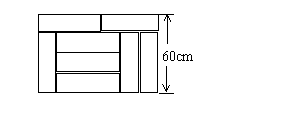
【解】设每块地砖的长为xcm，宽为ycm
根据题意，得
解这个方程组，得 
答：每块地砖的长为45cm，宽为15cm
12. 夏季，为了节约用电，常对空调采取调高设定温度和清洗设备两种措施。某宾馆先把甲、乙两种空调的设定温度都调高1℃，结果甲种空调比乙种空调每天多节电27度；再对乙种空调清洗设备，使得乙种空调每天的总节电量是只将温度调高1℃后的节电量的1.1倍，而甲种空调节电量不变，这样两种空调每天共节电405度。求只将温度调高1℃后两种空调每天各节电多少度？
【解】解法一：设只将温度调高1℃后，甲种空调每天节电x度，乙种空调每天节电y度
依题意，得：
解得：
答：只将温度调高1℃后，甲种空调每天节电207度，乙种空调每天节电180度。
解法二：设只将温度调高1℃后，乙种空调每天节电x度
则甲种空调每天节电
度
依题意，得：
解得：
答：只将温度调高1℃后，甲种空调每天节电207度，乙种空调每天节电180度。
13.解方程组：
【解】
把(x＋y)＝9代入②得3×9＋2x＝33 ∴x＝3
把x＝3代入①得y＝6
∴原方程组的解是
14.某酒店客房部有三人间、双人间客房，收费数据如下表．
为吸引游客，实行团体入住五折优惠措施．一个50人的旅游团优惠期间到该酒店入住，住了一些三人普通间和双人普通间客房．若每间客房正好住满，且一天共花去住宿费1510元，则旅游团住了三人普通间和双人普通间客房各多少间？
【解】设三人普通房和双人普通房各住了、间，
根据题意，得
解得
答：三人间普通客房、双人间普通客房各住了8、13间．
15.【05东营】某水果批发市场香蕉的价格如下表：
| 购买香蕉数 (千克) | 不超过 20千克 | 20千克以上 但不超过40千克 | 40千克以上 |
| 每千克价格 | 6元 | 5元 | 4元 |
张强两次共购买香蕉50千克（第二次多于第一次），共付出264元， 请问张强第一次、第二次分别购买香蕉多少千克？
【解】设张强第一次购买香蕉x千克，第二次购买香蕉y千克，
由题意可得0<x<25. 分
则①
当0<x≤20，y≤40时,由题意可得
解得
② 当0<x≤20，y＞40时,由题意可得
解得
(不合题意，舍去)
③ 当20<x<25时，则25<y<30．此时张强用去的款项为
(不合题意，舍去)
由①②③可知
张强第一次购买香蕉14千克，第二次购买香蕉36千克．
16.解方程组：
【解】
①+②得； 
把代人②得 
原方程组的解为
17.【05黄石】被誉为城区风景线的杭州东路跨湖段1857米，其各项绿化指标如表中所示，分析下表，回答下
列下列问题：
| 主要树种 | 株数 | 绿化覆盖率 |
| 香樟 | 336 | 24% |
| 柳树 | 188 | 12% |
| 棕榈 | 258 | 3% |
| 桂花树 | 50 | 1% |
| 合计 | 832 | 40% |
（1）已知杭州东路全长4744米，在各树行距（两树之间的水平距离）不变的情况下，请你用统计方法估计全线栽植的香樟、棕榈各多少株（结果保留整数）？
（2）杭州东路全线绿化工程是分期完成的，每千米的绿化投资成本一定。跨湖段是首期工程，且阳光、水份、土壤皆优于其它路段，问是否可能用跨湖段的绿化覆盖率40%表示全线的绿化覆盖率？请用统计知识说明理由。
【解】（1）由各树种行距不变，可知香樟、棕榈是均匀分布在杭州东路全线上。设全线香樟x株，棕榈y株，则
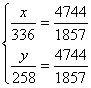解得
答：全线栽植香樟858株，棕榈659株。
（2）不能用跨湖段的绿化覆盖率40%表示全线的绿化覆盖率。
由于跨湖段的绿化是首期工程，树木栽植时间长，阳光、水份、土壤皆优于其它路段
所以跨湖段的绿化覆盖率不可能是全线绿化覆盖率的平均数，也不可能是中位数，故40%不能表示全线的绿化覆盖率。
选择题、填空题答案
一、选择题
1.C 2.A 3.A
课后反思