中考数学分类讨论题型整编
【知识整合创新】
整体感悟:分类讨论问题是创新性问题之一,此类题综合性强,难题较大,在各地中考试题中多以压轴题出现,对考生的能力要求较高,具有选拔性。目前,中考试卷中,觉见的需分类讨论的知识点有三大类:
1.代数类:代数有绝对值、方程及根的定义,函数的定义以及点(坐标未给定)所在象限等.
2.几何类:几何有各种图形的位置关系,未明确对应关系的全等或相似的可能对应情况等.
3.综合类:代数与几何类分类情况的综合运用.
特例探究:以性质、公式、定理的使用条件为标准分类的题型.
中考高分解密:
题型1.考查数学概念及定义的分类
规律提示:熟练掌握数学中的概念及定义,其中以绝对值、方程及根的定义,函数的定义尤为重要,必须明确讨论对象及原因,进而确定其存在的条件和标准。
考题1.求函数![]() 的图象与x轴的交点?
的图象与x轴的交点?
名师点拔:二次项系数中含有参数k,此函数可能是二次函数,也可能是一次函数,故应对![]() 分类讨论.
分类讨论.
解:(1)当![]() 时,即
时,即![]() 时,此函数为
时,此函数为![]() ,故其与x轴只有一个交点(1,0)
,故其与x轴只有一个交点(1,0)
(2)当![]() 时,此函数为二次函数,
时,此函数为二次函数,![]() .①当
.①当![]() 时,Δ=0.抛物线与x轴的交点只有一个.
时,Δ=0.抛物线与x轴的交点只有一个.![]() ,交点坐标为(1,0)②当
,交点坐标为(1,0)②当![]() 时,Δ>0,函数与x轴有两个不同的交点.
时,Δ>0,函数与x轴有两个不同的交点.![]() .
.
综合所述:当![]() 或
或![]() 时,函数图像与x轴只有一个交点(1,0);当
时,函数图像与x轴只有一个交点(1,0);当![]() 且
且![]() 时,函数图像与x轴有两个不同交点
时,函数图像与x轴有两个不同交点![]() .
.
变式思考1已知关于x的方程![]()
(1)若方程有实数根,求k的取值范围
(2)若等腰三角形ABC的边长a=3,另两边b和c恰好是这个方程的两个根,求ΔABC的周长.
易误点睛:根据方程定义确定方程到底是一次方程还是二次方程,同时应注意的是第(2)问中并无说明哪两边是ΔABC的腰,故应考虑其所有可能情况.
题型2:考查字母的取值情况或范围的分类.
规律提示:此类问题通常在函数中体现颇多,考查自变量的取值范围的分类,解题中应十分注意性质、定理的使用条件及范围.
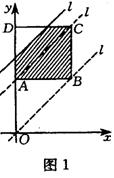
考题2.(2004,河南)如图(1)边长为2的正方形ABCD中,顶点A的坐标是(0,2)一次函数![]() 的图像
的图像![]() 随
随![]() 的不同取值变化时,位于
的不同取值变化时,位于![]() 的右下方由
的右下方由![]() 和正方形的边围成的图形面积为S(阴影部分).
和正方形的边围成的图形面积为S(阴影部分).
(1)当![]() 取何值时,S=3?
取何值时,S=3?
(2)在平面直角坐标系下(图2),画出S与![]() 的函数图像.
的函数图像.
名师点拔:设![]() 与正方形ABCD的交点为M,N,易知ΔDMN是等腰RtΔ,只有当MD=
与正方形ABCD的交点为M,N,易知ΔDMN是等腰RtΔ,只有当MD=![]() 时,
时,![]() ,那么
,那么![]() ,此时求得
,此时求得![]() ,第(2)问中,随着
,第(2)问中,随着![]() 的变化,S的表达式发生变化,因而须分类讨论
的变化,S的表达式发生变化,因而须分类讨论![]() 在不同取值时S的表达式,进而作出图像.
在不同取值时S的表达式,进而作出图像.
 解:(1)设
解:(1)设![]() 与正方形ABCD的交点为M,N,
与正方形ABCD的交点为M,N,
∵![]() 的解析式
的解析式![]() ,在x轴,y轴上所截线段相等.
,在x轴,y轴上所截线段相等.
∴ΔDMN为等腰RtΔDMN
∵S=3,∴![]()
又∵![]()
∴MD=ND=![]() ,∴ON=OD-DM=4-
,∴ON=OD-DM=4-![]() ,
,
即D点的坐标为(0,4-![]() )
)
 ∴
∴![]() ,即当
,即当![]() 时,S=3.
时,S=3.
(2)∵直线![]() 与
与![]() 轴的交点M的坐标为
轴的交点M的坐标为![]()
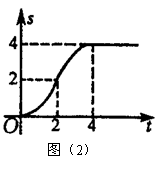
∴当0≤t<2时,![]()
当2≤t<4时,![]()
当t≥4时,S=4
根据以上解析式,作图如下图(图2)
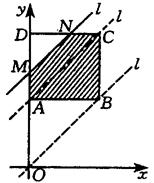
变式思考2 (2004 资阳)如图所示,在平行四边形ABCD中, ![]() ,
,
∠A=60°,BD⊥AD,一动点P从A出发,以每秒1cm的速度沿![]() 的路线匀速运动,过点P作直线PM,使PM⊥AD.
的路线匀速运动,过点P作直线PM,使PM⊥AD.
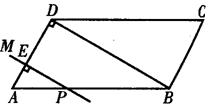 (1)当点P运动2秒时,设直线PM与AD相交于点E,求△APE的面积;
(1)当点P运动2秒时,设直线PM与AD相交于点E,求△APE的面积;
(2)当点P运动2秒时,另一动点Q也从A出发沿![]() 的路线运动,且在AB上以每秒1cm的速度匀速运动,在BC上以每秒2cm的速度匀速运动.过Q作直线QN,使QN//PM.设点Q运动的时间为t秒(0≤t≤10),直线PM与QN截平行四边形ABCD所得图形的面积为Scm2.
的路线运动,且在AB上以每秒1cm的速度匀速运动,在BC上以每秒2cm的速度匀速运动.过Q作直线QN,使QN//PM.设点Q运动的时间为t秒(0≤t≤10),直线PM与QN截平行四边形ABCD所得图形的面积为Scm2.
①求S关于t的函数关系式;②(附加题)求S的最大值.
易误点睛:讨论变量![]() 的取值范围,是解本题的关键,解此类题应十分注意变量的取值须符合题意,逐层分析.
的取值范围,是解本题的关键,解此类题应十分注意变量的取值须符合题意,逐层分析.
题型3.考查图形的位置关系或形状的分类.
规律提示:熟知直角三角形的直角,等腰三角形的腰与角以及圆的对称性,根据图形的特殊性质,找准讨论对象,逐一解决.
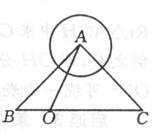 考题3.(2004 上海)在ΔABC中,∠BAC=90°,AB=AC=
考题3.(2004 上海)在ΔABC中,∠BAC=90°,AB=AC=![]() ,圆A的半径为1,如图所示,若点O在BC边上运动,(与点B和C不重合),
,圆A的半径为1,如图所示,若点O在BC边上运动,(与点B和C不重合),
设BO=x,ΔAOC的面积为![]() .
.
(1)求![]() 关于
关于![]() 的函数解析式,并写出函数的定义域.
的函数解析式,并写出函数的定义域.
(2)以点O为圆心,BO长为半径作圆O,求当圆O
与圆A相切时ΔAOC的面积.
名师点拔:(1)过点A作AD⊥BC于D点 ∵AB=AC=![]()
∴AD=![]() =2
=2
![]() ∴OC=BC-BO=4-x,故ΔAOC的面积
∴OC=BC-BO=4-x,故ΔAOC的面积![]() 与
与![]() 的函数解析式为
的函数解析式为![]() 即
即![]() (2)由于圆与圆相切有两种情况:外切和内切,故解题中须分类讨论.
(2)由于圆与圆相切有两种情况:外切和内切,故解题中须分类讨论.
解:(1)过点A作AD⊥BC于点D.
∵∠BAC=90° AB=AC=![]() ∴BC=4 AD=
∴BC=4 AD=![]() BC=2
BC=2
∴![]()
即![]()
(2)当点O与点D重合时,圆O与圆A相交,不合题意;当点O与点D不重合时,在RtΔAOD中,![]()
∵⊙A的半径为1,⊙O的半径为x
∴①当⊙A与⊙O外切时
![]() 解得
解得![]()
此时,ΔAOC的面积![]()
②当⊙A与⊙O内切时,![]() 解得
解得![]()
此时ΔAOC的面积![]()
∴当⊙A与⊙O相切时,ΔAOC的面积为![]() .
.
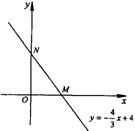 变式思考3(2003 南京)如图,直线
变式思考3(2003 南京)如图,直线![]() 与x轴,y轴分别交于点M,N
与x轴,y轴分别交于点M,N
(1)求M,N两点的坐标;
(2)如果点P在坐标轴上,以点P为圆心,
![]() 为半径的圆与直线
为半径的圆与直线![]() 相切,求点P的坐标.
相切,求点P的坐标.
易误点睛:本题是一道函数与圆的综合题,注意第(2)
小问涉及到分类讨论,与直线相切时的情况,本题可分为两大类,四小类,切勿漏掉,解决此类问题关键是把握标准,正确的分类.
题型4.考查图形的对应关系可能情况的分类
规律提示:图形的对应关系多涉及到三角形的全等或相似问题,对其中可能出现的有关角、边的可能对应情况加以分类讨论.
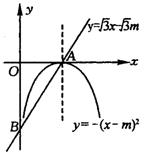 考题4(2004 福州)如图所示,抛物线
考题4(2004 福州)如图所示,抛物线![]() 的顶点为A,直线
的顶点为A,直线![]() 与y轴的交点为B,其中m>0.
与y轴的交点为B,其中m>0.
(1)写出抛物线对称轴及顶点A的坐标
(用含有m的代数式表示)
(2)证明点A在直线![]() 上,并求∠OAB的度数.
上,并求∠OAB的度数.
(3)动点Q在抛物线的对称轴上,则抛物线上是否存在点P,使以P、Q、A为顶点的三角形与△OAB全等?若存在,求出m的值,并写出所有符合上述条件的P点坐标;若不存在,说明理由.
名师点拨:(1)对称轴![]() ,顶点A(m,0)(2)把x=m代入
,顶点A(m,0)(2)把x=m代入![]() 得
得![]() ∴点A(m,0)在直线
∴点A(m,0)在直线![]() 上,直线
上,直线![]() 与y轴相交,则B点的横坐标为:
与y轴相交,则B点的横坐标为:![]() ;B点坐标为
;B点坐标为![]() ,由三角函数知识可得:
,由三角函数知识可得:![]()
即∠OAB=60° (3)因为全等的对应关系,因而需进行分类论,找准对应关系,从而解决问题。
解:(1)对称轴为直线![]() ,顶点A(m,0)
,顶点A(m,0)
(2)把![]() 代入函数
代入函数![]()
∴点A(m,0)在直线![]() 上.当x=0时,
上.当x=0时,![]()
∴![]() ∴∠OAB=60°
∴∠OAB=60°
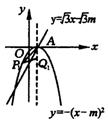
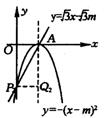
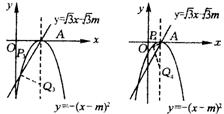
(3)如图,以P、Q、A为顶点的三角形与ΔOAB全等,共有以下4种情况:
①![]() ∴
∴![]() 点的坐标为
点的坐标为![]() ,代入抛物线解析式得:
,代入抛物线解析式得:![]() ∴
∴![]() ∴
∴![]()
②![]() ∴
∴![]()
∴![]() ∴
∴![]()
③![]() ∴
∴![]() 点的坐标为
点的坐标为![]() 代入抛物线解析式得:
代入抛物线解析式得:![]() ∴
∴![]() ∴
∴![]()
④![]() ∴
∴![]() 点的坐标为
点的坐标为![]() ,代入抛物线解析式得:
,代入抛物线解析式得:![]() ∴
∴![]() ∴
∴![]()
分析可知,![]() 关于抛物线对称轴的对称点均符合题意;
关于抛物线对称轴的对称点均符合题意;
综上所述,符合条件的P点分别为![]() ;(0,3),
;(0,3),![]() ,
,![]() ,
,![]() .
.
变式思考4(2003宁波)已知抛物线![]() 的顶点坐标为(4,-1)与y轴交于点C(0,3),O是原点.
的顶点坐标为(4,-1)与y轴交于点C(0,3),O是原点.
(1)求这条抛物线的解析式.
(2)设此抛物线与x轴的交点A、B(A在B的左边),问在y轴上是否存在点![]() ,使以O,B,P为顶点的三角形与ΔAOC相似?若存在,请求出点P的坐标,若不存在,请说明理由.
,使以O,B,P为顶点的三角形与ΔAOC相似?若存在,请求出点P的坐标,若不存在,请说明理由.
易误点睛:解决此类问题,必须对三角形全等或相似的性质烂熟于心,对两三角形的对应角(或边)进行分类讨论,逐步找到符合题意的结论.
中 考 零 距 离
一、选择题
1.若m为实数,则点P(m-2,m+2)不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.相交两圆公共弦长为6,两圆的半径分别为![]() ,5,则这两圆的圆心距等于( )
,5,则这两圆的圆心距等于( )
A.1 B.2或6 C.7 D.1或7
3.(2004,河南)如果关于x的方程![]() 的两个根的差为1,那么m等于( )
的两个根的差为1,那么m等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.平面上A、B两点到直线![]() 的距离分别是
的距离分别是![]() ,则线段AB的中点C到直线
,则线段AB的中点C到直线![]() 的距离是( )
的距离是( )
A.2 B.![]() C.2或
C.2或![]() D.不能确定
D.不能确定
5.已知![]() 是完全平方式,则m的值是( )
是完全平方式,则m的值是( )
A.-3 B.10 C.-4 D.10或-4
二、填空题
6.已知AB是⊙O的直径,AC、AD是弦,且AB=2,AC=![]() ,AD=1,则∠CAD=_______.
,AD=1,则∠CAD=_______.
7.已知AB、CD是⊙O的两条平行线,AB=12,CD=16,⊙O的直径为20,则AB与CD之间的距离为________.
8.方程![]() 的最大根与最小根的积为______.
的最大根与最小根的积为______.
9.(2004 上海)直角三角形的两条边长分别为6和8,那么这个三角形的外接圆半径等于________.
10.(2004 沈阳)已知ΔABC中,∠C=90°,AC=3,BC=4,分别以A和C为圆心作⊙A和⊙C,且⊙C与直线AB不相交,⊙A与⊙C相切,设⊙A的半径为r,那么r的取值范围是______.
11.已知![]() ,则
,则![]() 的值等于_______.
的值等于_______.
12.在平面直角坐标系内,A、B、C三点的坐标分别是(0,0),(4,0),(3,2),以A、B、C三点为顶点画平行四边形,则第四个顶点不可能在第_____象限.
三、解答题
13.(2004 广东)已知实数a,b分别满足![]() 的值.
的值.
14.(2004 黑龙江)在劳技课上,老师请同学们在一张长为17cm,宽16cm的长方形纸板上剪下一个腰长为10cm的等腰三角形(要求等腰三角形的一个顶点与长方形的一个顶点重合,其余两个顶点在长方形上的边上)请你帮助同学们计算剪下的等腰三角形的面积.
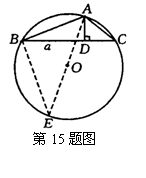
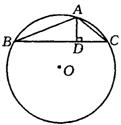 15.(2004 芜湖)在钝角△ABC中,AD⊥BC,垂足为D点,且Ad与DC的长度为
15.(2004 芜湖)在钝角△ABC中,AD⊥BC,垂足为D点,且Ad与DC的长度为![]() 方程的两个根,⊙O是△ABC的外接圆,如果BD长为
方程的两个根,⊙O是△ABC的外接圆,如果BD长为![]() .求△ABC的外接圆⊙O的面积.
.求△ABC的外接圆⊙O的面积.
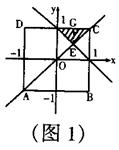
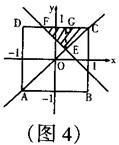
16.(2003 烟台)在直角坐标系中,有以A(-1,-1),B(1,-1),C(1,1),D(-1,1)为顶点的正方形,设正方形在直线y=x上方及直线
y=-x+2a上方部分的面积为S,(1)求![]() 时,S的值.(2)a在实数范围内变化时,求S关于a的函数关系式.
时,S的值.(2)a在实数范围内变化时,求S关于a的函数关系式.
17.(2004 黄冈)在直角坐标系XOY中,O为坐标原点,A、B、C三点的坐标分别为A(5,0),B(0,4),C(-1,0),点M和点N在x轴上,(点M在点N的左边)点N在原点的右边,作MP⊥BN,垂足为P(点P在线段BN上,且点P与点B不重合)直线MP与y轴交于点G,MG=BN.
(1)求经过A、B、C三点的抛物线的解析式.(2)求点M的坐标.
(3)设ON=t,△MOG的面积为S,求S与t的函数关系式,并写出自变量t的取值范围.
(4)过点B作直线BK平行于x轴,在直线BK上是否存在点R,使△ORA为等腰三角形?若存在,请直接写出R的坐标;若不存在,请说明理由.
变式思考答案
1.解:(1)∵方程有实数根.∴①当k=0时,原方程变为![]() ,方程有实数根.
,方程有实数根.
②当![]() 时,
时,![]() ,解之得
,解之得![]() ,∴
,∴![]() 故k的取值范围是
故k的取值范围是![]() .
.
(2)①若b=c,则![]() ,解得
,解得![]() ,此时方程的根为b=c=2,又∵a=3,满足三角形三边关系,∴
,此时方程的根为b=c=2,又∵a=3,满足三角形三边关系,∴![]()
②若a=b或a=c,则![]() ,∴
,∴![]() ,此时方程另一根为:
,此时方程另一根为:![]() ,满足三角形三边关系,∴
,满足三角形三边关系,∴![]() .
.
2.(1)当点P运动2秒时,AP=2cm,由∠A=60°,知AE=1,PE=![]() .∴
.∴![]() .
.
(2)①(i)当0≤t≤6时,点P与点Q都在AB上运动,设PM与AD交于点G,QN与AD交于点F,则AQ=t,AF=![]() ,QF=
,QF=![]() ,AP=t+2,AG=1+
,AP=t+2,AG=1+![]() ,PG=
,PG=![]() .
.
∴此时两平行线截平行四边形ABCD的面积为![]() .
.
(ii)当6≤t≤8时,点P在BC上运动,点Q仍在AB上运动,设PM与DC交于点G,QN与AD交于点F,则AQ=t,AF=![]() ,DF=4-
,DF=4-![]() ,QF=
,QF=![]() ,BP=t-6,
,BP=t-6,
CP=10-t,PG=(10-t)![]() .
.
而BD=![]() ,故此时两平行线截平行四边形ABCD的面积为
,故此时两平行线截平行四边形ABCD的面积为![]() .
.
(iii)当8≤t≤10时,点P和点Q都在BC上运动,设PM与DC交于点G,QN与DC交于点F,则CQ=20-2t,OF=(20-2t),CP=10-t,PG=(10-t)![]() .
.
∴此时两平行线截平行四边形ABCD的面积为![]() .
.
故S关于t的函数关系式为
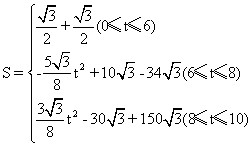
②(附加题)当0≤t≤6时,S的最大值为![]() ;
;
当6≤t≤8时,S的最大值为![]() .
.
当8≤t≤10时,S的最大值为![]()
所以当t=8时,S有最大值为![]() .
.
3.解:(1)当x=0时,y=4. 当y=0时,![]() ,∴x=3.
,∴x=3.
∴M(3,0),N(0,4)
(2)①当![]() 点在y轴上,并且在N点的下方时,设⊙
点在y轴上,并且在N点的下方时,设⊙![]() 与直线
与直线![]() 相切于点A,连接
相切于点A,连接![]() A,则
A,则![]() A⊥MN.
A⊥MN.
∴∠![]() AN=∠MON=90°,∵∠
AN=∠MON=90°,∵∠![]() NA=∠MNO,∴△
NA=∠MNO,∴△![]() AN∽△MON,∴
AN∽△MON,∴![]()
在Rt△OMN中,OM=3,ON=4,∴MN=5.
又∵![]() ,∴
,∴![]() ,∴
,∴![]() 点坐标是(0,0)
点坐标是(0,0)
②![]() 点在x轴上,并且在M点的左侧时,同理可得
点在x轴上,并且在M点的左侧时,同理可得![]() 点坐标是(0,0)
点坐标是(0,0)
③当![]() 在x轴上,并且在M点的右侧时,设⊙
在x轴上,并且在M点的右侧时,设⊙![]() 与直线
与直线![]() 相切于点B,连接
相切于点B,连接![]() ,则
,则![]() ∴OA//
∴OA//![]() . ∵OA=
. ∵OA=![]() ,∴
,∴![]() .
.
∴![]() ,∴
,∴![]() 点坐标是(6,0)
点坐标是(6,0)
④当![]() 点在y轴上,并且在点N上方时,同理可得
点在y轴上,并且在点N上方时,同理可得![]() .
.
∴![]() . ∴
. ∴![]() 点坐标是(0,8)
点坐标是(0,8)
综上,P点坐标是(0,0),(6,0),(0,8).
4.解:(1)可设![]() . ∵交y轴于点C(0,3),∴3=16a-1,∴
. ∵交y轴于点C(0,3),∴3=16a-1,∴![]() .
.
∴抛物线的解析式为![]() ,即
,即![]() .
.
(2)存在
当y=0时,则![]() ,∴
,∴![]() ∴A(2,0),B(6,0).
∴A(2,0),B(6,0).
设P(0,m),则OP=![]() . 在△AOC与△BOP中,
. 在△AOC与△BOP中,
①若∠OCA=∠OBP,则△BOP∽△COA,∴![]() .
.
OP=![]() ,∴
,∴![]() .
.
②若∠OCA=∠OPB,则△BOP∽△AOC,∴![]() .
.
![]() ,∴
,∴![]() .
.
∴存在符合题意的点P,其坐标为(0,4)、(0,-4)、(0,9)或(0,-9)
中考零距离答案
一、选择题
1.C 2.D 3.C 4.C 5.D
二、填空题
6.15°或105° 7.14或2 8.3 9.4或5 10.![]()
11.![]() 12.三
12.三
三、解答题程
13.解:若![]() ,则可知
,则可知![]() 为方程
为方程![]() 的两实数根,由韦达定理得a+b=-2,ab=-2. ∴
的两实数根,由韦达定理得a+b=-2,ab=-2. ∴![]()
若![]() ,则解关于a,b的方程分别得
,则解关于a,b的方程分别得![]()
![]() .
.
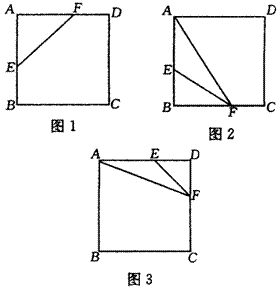 14.解:分三种情况计算:
14.解:分三种情况计算:
(1)当AE=AF=10cm时,(如图1),
![]()
(2)当AE=EF=10cm时(如图2),
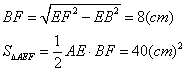
(3)当AE=EF=10cm时(如图3),
![]()
![]() .
.
15.解:∵AD与DC的长度为![]() 的两根 ∴有两种情况
的两根 ∴有两种情况
①AD=3,DC=4 ②AD=4,DC=3
由勾股定理:求得AC=5,连接AO并延长交⊙O于E点,
连接BE∴∠ABE=90° 又∵∠E=∠C
∴△ABE∽△ADC,
 ∴
∴![]()
16.解:(1)当![]() 时,如图1,
时,如图1,
直线![]() 的交点是
的交点是![]()
∴![]()
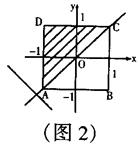 (2)①当
(2)①当![]() 时,如图2,
时,如图2,
△ADC的面积就是S,
∴![]()
②当-1≤a<0时,如图3,
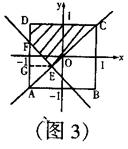 直线
直线![]() 的交点是E(
的交点是E(![]() ,
,![]() )
)
∴EG=(1-![]() )=1+a AF=2(1+a)
)=1+a AF=2(1+a)
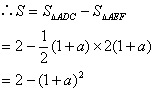
 ③当0≤a<1时,如图4,
③当0≤a<1时,如图4,
直线![]() 的交点是E(a,a)
的交点是E(a,a)
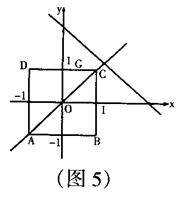 ∴EG=1-a CF=2(1-a)
∴EG=1-a CF=2(1-a)
∴![]()
④当a≥1时,如图5,S=0
∴S关于a的函数关系式为
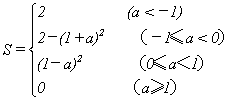
17.(1)设所求抛物线的解析式为![]() .
.
由题意,得: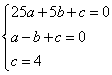 解得:
解得: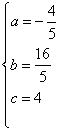
∴所求的解析式为![]() .
.
(2)依题意,分两种情况:
①当点M在原点的左边(如图1)时,
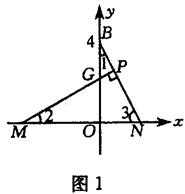 在Rt△BON中,∠1+∠3=90°
在Rt△BON中,∠1+∠3=90°
∵MP⊥BN,∴∠2+∠3=90°
在Rt△BON和Rt△MOG中,
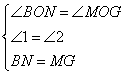
∴Rt△BON≌Rt△MOG. ∴OM=OB=4
∴M点坐标为(-4,0)
②当点M在原点的右边(如图2)时,同理可证:OM=OB=4.
此时M点的坐标为(4,0)
∴M点的坐标为(-4,0)或(-4,0)
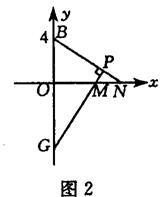 (3)图1中,Rt△BON≌Rt△MOG. ∴OG=ON=t.
(3)图1中,Rt△BON≌Rt△MOG. ∴OG=ON=t.
∴S=![]() (其中0<t<4)
(其中0<t<4)
图2中,同理可得S=2t,其中t>4.
∴所求的函数关系式为S=2t.
t的取值范围为t>0且t ![]() 4.
4.
(4)存在点R,使△ORA为等腰三角形.
其坐标为:![]() .
.