初三
数学第一学期第二次统测
数 学 试 卷
说明：全卷满分为120分，考试时间为90分钟。
一、选择题：（每小题3分，共15分）
1、点M(－sin60°，cos60°)关于x轴对称的点的坐标是（ ）
A．(
) B．(－
) C．(－
,
) D．(－
,-)
2、下列各点中，在函数
的图象上的是（ ）．
(A)（2，3） （B）（3，1） （C）（0，-7） （D）（一1，9）
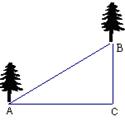
3、如图，在山坡上种树，已知∠A=30°，AC=3米，则相邻两株树的坡面距离AB=（ ）
A、6米 （B）
米 （C）2米 （D）2
米
4、用换元法解分式方程
时，如果设
，那么将原方程化为关于y的一元二次方程的一般形式是（ ）
A、
B、
C、
D、
5、已知直角三角形的两条直角边的长恰好是方程
的两根，则此直角三角形的斜边长为( ).
A、
B、3 C、
D、13
二、填空题：（每小题4分，共20分）
6、请写出一元二次方程
＝0的一个常数项，使这个方程有两个不相等的实数根。
7、在函数
中，自变量
的取值范围是_______________
8、若
、
为方程
的两根，则
＝ ．
9、一次函数
的图象不经过第 象限.
10、如右图，修建抽水站时，沿着倾斜角为300的斜坡铺设管道，若量得水管AB的长度为80米，那么点B离水平面的高度BC的长为 米。
三、解答下列各题：（每小题6分，共30分）
11、
12、解方程组：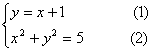
13、在Rt△ABC中, ∠C=90°，斜边
，两直角边的长
，
是关于
的一元二次方程
的两个根，求Rt△ABC中较小锐角的正弦值。
14、已知△ABC.
求作：△ABC的外接圆⊙Ｏ（要求：不写作法，只保留作图痕迹）
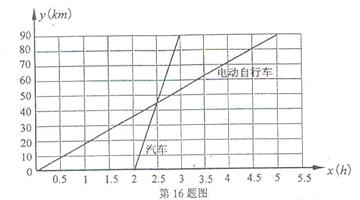
15、如图，表示甲骑电动车和乙驾驶汽车均行驶90km过程中，行驶的路程y与经过的时间x之间的函数关系式.请根据图象填空：
（1） 出发的早，早了 小时；
（2） 先到达，先到 小时；
（3）电动自行车的速度为 km/h，汽车的速度为 km/h.
四、解答题（每小题7分，共28分）
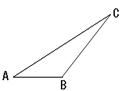
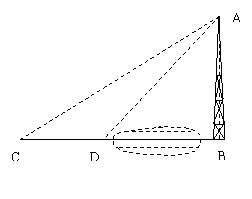16、如图，河对岸有一铁塔AB。在C处测得塔顶A的仰角为30°，向塔前进16米到达D，在D处测得A的仰角为45°，求铁塔AB的高。
17、已知方程
的两个实数根是
、
，是否存在
的值，使得、满足
？若存在，求出的值；若不存在，请说明理由.
解：存在满足题意的值。
由一元二次方程的根与系数的关系得
，
∴
∵
∴
阅读后回答下列问题：上面的解题过程是否正确？若不正确，写出正确的解题过程.
18、为了确保我市国家级卫生城市的称号，市里对主要街道的排污水沟进行改造. 其中光明施工队承包了一段要开挖96米长的排污水沟，开工后每天比原计划多挖2米，结果提前4天完成任务，问原计划每天挖多少米？
19、已知一次函数的图象经过A（-2，-3），B（1，3）两点.
（1）求这个一次 函数的解析式
（2）试判断点P（-1，1）是否在这个一次函数的图象上？
五、解答题：（每小题9分，共27分）
20、已知：关于
的方程
（1）当取何值时，方程有两个实数根？
（2）为选取一个合适的整数，使方程有两个不相等的实数根，并求这两个根；
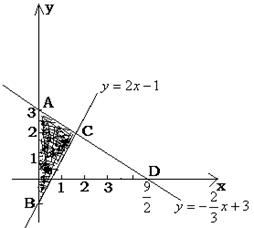
21、如图已知两直线
和
，求它们与
轴所围成的三角形的面积。
22、随着海峡两岸交流日益增强，通过“零关税”进入我市的一种台湾水果，其进货成本是每吨0.5万元，这种水果市场上的销售量（吨）是每吨的销售价（万元）的一次函数，且
时，
；
时，
。
（1）求出销售量（吨）与每吨的销售价（万元）之间的函数关系式；
（2）若销售利润为
（万元），请写出与之间的函数关系式，并求出销售价为每吨2万元时的销售利润。
备选题
已知
是一元二次方程
的两个实根。
（1）求实数的取值范围；
（2）如果满足不等式
，且为整数。求的值。
22、已知关于x的方程 kx2-2 (k+1) x+k-1=0 有两个不相等的实数根，
(1) 求k的取值范围；
(2) 是否存在实数k，使此方程的两个实数根的倒数和等于0 ？若存在，求出k的值；若不存在，说明理由.