中考数学总复习专题训练（十一)粤教

中考数学总复习专题训练（十一)　

 （解直角三角形）

考试时间：120分钟 满分150分

一、选择题（每小题3分，共45分）

1.当锐角A<60⁰时,下列结论不正确的是（　 ）。

Ａ．sinA<­­ 　Ｂ．cosA<­­　　­Ｃ．tanA<­­　　­Ｄ．cotA>­­

2.若A为锐角,且sinA=­­,则角A满足（　 ）。

Ａ．0⁰<A<30⁰Ｂ．­30⁰<A<45⁰Ｃ．­45⁰<A<60⁰Ｄ．­60⁰<A<90⁰

3.若sin²40⁰+sin²α=1,且α为锐角,则α等于（　 ）。

Ａ．30⁰ Ｂ．40⁰ Ｃ．­50⁰ Ｄ．­60⁰

4.在RtΔABC中,∠C=90⁰,则下列等式中不正确的是（　 ）。

Ａ．a=csinA　  Ｂ．­a=bcotB　　　Ｃ．­b=csinB　　Ｄ．c=­­

5.若ΔABC中,锐角A满足­丨sinA－­­丨+cos²C=0.则ΔABC是（　 ）。

­Ａ．等腰直角三角形　　　　　　  Ｂ．等腰三角形

Ｃ．直角三角形　　　　　　　　  Ｄ．锐角三角形

6.在RtΔABC中,∠C=90⁰,sinA=­­,b=8,则c=（　 ）。

Ａ．6　　　　  Ｂ．­10　　　　　 Ｃ．25　　　　　 Ｄ．50.

7.等腰三角形的面积为40,底边长4,则底角的正切值为（　 ）。

Ａ．­10　　　　  Ｂ．20　　　　  Ｃ．­　　　　　 Ｄ．­­

8.若0⁰<A<90⁰,且cosA的值是方程2x²－3x+1=0的一个根,则cosA的值为（　 ）。

Ａ．­­　　　　　 Ｂ．­1­　　　　　 Ｃ．1或2　　　　 Ｄ．­­或1

9.AD是ΔABC的高,AD在ΔABC的外部,AD=BD=1,DC=­­,则∠BAC=（　 ）。

Ａ．15⁰ Ｂ．­60⁰ Ｃ．105⁰  Ｄ．15⁰或105⁰

10.在ΔABC中,∠C=90⁰,点D在AC上,且AD=BD,BC=3,DC=4,∠BDC=α,则cot­=（　 ）。

Ａ．­­　　　　　 Ｂ．­­　　　　　 Ｃ．­3　　　　 Ｄ．­­

11.ΔABC中,∠C=90⁰,∠BAC=30⁰,AD是中线,则tan∠CDA=（　 ）。

Ａ．­­　　　　  Ｂ．2­­　　　　 Ｃ．3­­　　　Ｄ．­

12.在Rt△ABC中，∠C=90°，若sinA=，则tanB=（　 ）。

　Ａ．　　  　　　 Ｂ．　　　　Ｃ．　　 Ｄ．

13.在△ABC中，若sinA－+(1－tanB)²=0，则∠C的度数是（　 ）。

Ａ．45°　　　　　  Ｂ．60°　 　　Ｃ．75°　　　 Ｄ．105°

14.a=sin60º，b=cos45º，c=tan30º，则它们之间的大小关系是（　 ）。

Ａ．c<b<a　　　　　 Ｂ．b<a<c　　 Ｃ．a<c<b　　　Ｄ．b<c<a

15.某人沿着坡度为1∶的山坡前进了1000 m，则这个人所在的位置升高了（　 ）。

Ａ．1000 m　　　　 Ｂ．500 m　　  Ｃ．500 m　 Ｄ． m

二、填空题（每小题3分，共24分）

1.若2cos(α+15⁰)=1,则cotα=_________。

2.若平行四边形ABCD中,AB=3,BC=4,∠B=30⁰,则平行四边形ABCD的面积为_________。

3.在ΔABC中,∠C=90⁰,AD是角平分线, AC=24,AD=16­­, 则cos∠CAB=

_________。

4.在RtΔABC中,∠C=90⁰,4a=3b,则sinA=_________。

5.有一拦水坝的横断面是等腰梯形，它的上底长为6米，下底长为10米，高为2米，那么此拦水坝斜坡的坡度为_________，坡角为_________。

6.已知tanα·tan30°=1，且α为锐角，则α=_________。

7.菱形的两条对角线长分别为2和6，则菱形的相邻的两内角分别为_________。

8.一次函数y=ax+b的图象过点P(1，2)，且与x轴正半轴交于点A，与y轴正半轴交于B，若tan∠PAO=，则点B的坐标是_________。

三、解答下列各题（每题9分，共 81分）

1.计算或化简：

(1)cos30°+sin45°；

(2)·tan 30°；

(3)(sin60°+cos 45°)(sin 60°－cos 45°)；

2．如图，在Rt△ABC中，∠C=90°，D是BC边上一点，AC=2，CD=1，设∠CAD=α.

(1)求sinα、cosα、tanα的值；

(2)若∠B=∠CAD，求BD的长.。

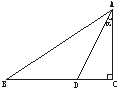
3. 如图，在ΔABC中,∠B=60⁰,∠C=45⁰,BC=20。求ΔABC的面积。

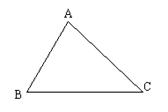
4.如图，水库大坝的横断面为梯形，坝顶宽6米，坝高24米，斜坡AB的坡角为45º，斜坡CD的坡比为i＝1：2，则坝底宽BC为多少米？

　

5.RtΔABC中,∠C=90⁰,sinA和cosB是关于x的方程kx²－kx+1=0的两个根,求∠B的度数。

6.等腰三角形的底边长20 cm，面积为 cm²，求它的各内角。

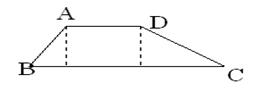
7.如图,ΔABC中,CD是中线,且CD⊥CA,CD=3,tan∠BCD=­­,求ΔABC各边的长。

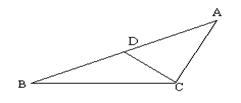
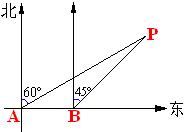
8.如图, 海上有一灯塔P, 在它周围3海里处有暗礁. 一艘客轮以9海里/时的速度由西向东航行, 行至A点处测得P在它的北偏东60⁰的方向, 继续行驶20分钟后, 到达B处又测得灯塔P在它的北偏东45⁰方向. 问客轮不改变方向继续前进有无触礁的危险?

9. “希望中学”有一块三角形形状的花圃ABC，现在可直接测量到：AC= 40 m，BC=25 m，∠A=30°，请求出这块花圃的面积。

参考答案

一、1、B 　 2、B　 3、C　　4、D　　5、A　　6、B　　7、A　 8、A

9、A　 10、C　 11、B　12、D　　13、C　 14、A　 15、B

二、1、1；2、6；3、； 4、；5、，60°；　6、60°；7、60°、120°；8、(0，)。　

三、1、(1)， (2) ， (3) 。

2、(1)sinα=，cosα=，tanα=。

(2)∵∠B=α，∠C=90°,

∴△ABC∽△DAC_.

∴=.∴BC==4。

则BD=BC－CD=4－1=3。

3、300－100。

4、分别过A、D作BC的垂线，垂足为E，F

　　∵∠B=45º，∴BE=AE=24，

　　∵斜坡CD的坡比为i＝1：2，

　　∴FC=2DF=2×24=48，　　　　　　 

　　∴BC=BE+EF+CF=78。

5、∠B=60°。提示：sinA=cosB，方程有等根，⊿=0。

6、设等腰三角形底边上的高为x cm，底角为α，则有x·20=,

∴x=。

∵tanα == ,∴∠α＝30°。

顶角为180°－2×30°=120°。

∴该等腰三角形三个内角为30°，30°，120°。

7、AB=；AC=2；BC=。

8、过P作PC⊥AB于C点, 据题意知:

AB=9=3, ∠PAB=90⁰－60⁰=30⁰

∠PBC=90⁰－45⁰=45⁰, ∠PCB=90⁰ 　

∴PC=BC

在Rt△ABC中: tan30⁰=

即：　∴PC=>3　

∴客轮不改变方向继续前进无触礁危险。

9、作CD⊥AB于D。

∵∠A=30°,

∴CD=AC=×40=20(m),

AD==20(m),

BD==15(m).

(1)当∠ACB为钝角时，AB=AD+BD=20+15,

∴S_△ABC=AB·CD=(20+15)×20=(200+150)(m²).

(2)当∠ACB为锐角时，AB=AD－BD=20－15.

∴S_△ABC=AB·CD=(20－15)×20=(200－150)(m²).