中考数学总复习专题训练（四)
（函数及其图象）
考试时间：120分钟 满分150分
一、选择题（每小题4分，共52分）
1．一次函数y=3x-1的图象不经过（ ）。
A．第一象限 B．第二象限 C．第三象限 D．第四象限
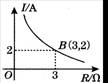2．某闭合电路中，电源电压为定值，电流I（A）与电阻R（Ω）成反比例．如图表示的是该电路中电流I与电阻R之间函数关系的图象，则用电阻R表示电流I的函数解析式为（ ）。
A．I＝ B．I＝－
C．I＝ D．I＝
3．函数
和函数y=x的图象在同一平面直角坐标系内的交点个数是（ ）。
A.1个 B.2个 C.3个 D.0个
4．设A（x1,y1）、B（x2,y2）是反比例函数y=
图象上的两点，若x1<x2<0,则y1与y2之间的关系是（ ）。
A. y2<y1<0 B. y1<y2<0 C. y2>y1>0 D. y1>y2>0
5．已知方程组
的解为
，则函数y=2x+3与y=
x+
的交点坐标为（ ）。
A．（l，5） B．（－1，1） C．（l，2）D．（4，l）
6．反比例函数
的图象在二、四象限，则k的取值范围是（ ）。
A．K≤3 B．K≥-3 C．K＞3 D．K＜-3.
7．当k＜0时，反比例函数y＝
和一次函数y＝kx＋2的图象大致是图中的（ ）。
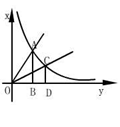8．如图，正比例函数y=x和y=mx的图象与反比例函数y＝
的图象分别交于第一象限内的A、C两点，过A、C分别向x轴作垂线，垂足分别为B、D.若直角三角形AOB与直角三角形COD的面积分别为S1、S2，则S1与S2的关系为（ ）。
A．S1>S2 B. S1=S2
C. S1<S2 D.与m、k的值有关
9．抛物线y=x2-2x+1的对称轴是（ ）。
A．直线x=1 (B)直线x=-1 (C)直线x=2 (D)直线x=-2
10．抛物线y=x2的图象向左平移2个单位，再向下平移1个单位，则所得抛物线的解析式为（ ）。
A .y=x2+4x+3 B. y=x2+4x+5
C. y=x2－4x+3 D .y=x2－4x－5
11．无论m为任何实数，二次函数y=x2+(2－m)x+m的图象总过的点是（ ）。
A.(－1，0) B.(1，0) C.(－1，3) D.(1，3)
12．无论m为何实数，直线
与
的交点不可能在（ ）。
A.第一象限 B.第二象限 C.第三象限 D.第四象限
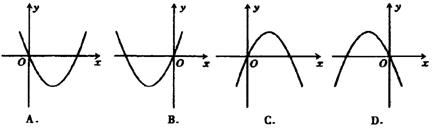
13．在反比例函数y=
中，当x＞0时，y随x的增大而增大，则二次函数y=kx2+2kx的图像大致是（ ）。
 |
二、填空题（每小题4分，共32分）
1．直线y=3x+6与x轴的交点的横坐标x的值是方程2x+a=0的解，则a的
值是_________。
2．点A(1,m)在函数y=2x的图象上，则点A关于y轴的对称的点的坐标为_________。
3．已知函数
是一次函数，则m=_________，此函数图象经过第_________象限。
4．若函数y=
是反比例函数，则k=_________。
5．已知y与x＋l成正比例，当x=5时,y＝12，则y关于x的函数解析式是
6.二次函数y=mx2＋2x＋m－4m2的图象过原点，则此抛物线的顶点坐标是_________。
(－4，－4)
7.已知抛物线y=ax2+bx+c的图象顶点为(－2，3)，且过(－1，5)，则抛物线的表达式为_________。
8.如果抛物线y=－2x2+mx－3的顶点在x轴正半轴上，则m=_________。
三、解答下列各题（每小题11分，共66分）
1.某电信公司开设了甲、乙两种市内移动通信业务。甲种使用者每月需缴15元月租费, 然后每通话1分钟, 再付话费0.3元; 乙种使用者不缴月租费, 每通话1分钟, 付话费0.6元。若一个月内通话时间为x分钟, 甲、乙两种的费用分别为y1和y2元.
(1)试分别写出y1、y2与x之间的函数关系式;
(2)在同一坐标系中画出y1、y2的图像;
(3)根据一个月通话时间, 你认为选用哪种通信业务更优惠?
2.某商场将每件进价为80元的某种商品原来按每件100元出售，一天可售出100件．后来经过市场调查，发现这种商品单价每降低1元，其销量可增加10件．
（1）求商场经营该商品原来一天可获利润多少元？
（2）设后来该商品每件降价x元，，商场一天可获利润y元．
①若商场经营该商品一天要获利润2160元，则每件商品应降价多少元？
②求出y与x之间的函数关系式，并通过画该函数图像的草图，观察其图像的变化趋势，结合题意写出当x取何值时，商场获利润不少于2160元？
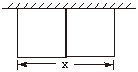
3.如图，要建一个长方形养鸡场，鸡场的一边靠墙，如果用50 m长的篱笆围成中间有一道篱笆隔墙的养鸡场，设它的长度为x m.
(1)要使鸡场面积最大，鸡场的长度应为多少m？
(2)如果中间有n(n是大于1的整数)道篱笆隔墙，要使鸡场面积最大，
鸡场的长应为多少m？比较(1)(2)的结果，你能得到什么结论？
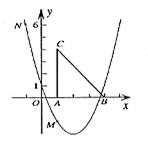
4.如图，二次函数
的图象经过点M（1，—2）、N（—1，6）。
（1）求二次函数的关系式。（3分）
（2）把Rt△ABC放在坐标系内，其中∠CAB = 90°，点A、B的坐标分别为（1，0）、（4，0），BC = 5。将△ABC沿x轴向右平移，当点C落在抛物线上时，求△ABC平移的距离。（4分）
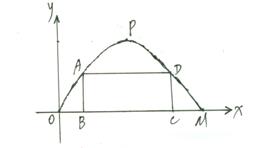
5.施工队要修建一个横断面为抛物线的公路隧道，其高度为6米，宽度OM
为12米.现以O点为原点，OM所在直线为X轴建立直角坐标系（如图所
示）。
（1）直接写出点M及抛物线顶点P的坐标；
（2）求出这条抛物线的函数解析式；
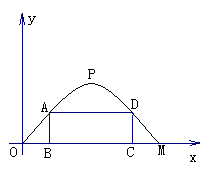（3）施工队计划在隧道门口搭建一个矩形“脚手架”CDAB，使A、D点在抛物线上，B、C点在地面OM上．为了筹备材料，需求出“脚手架”三根木杆AB、AD、DC的长度之和的最大值是多少？请你帮施工队计算一下.
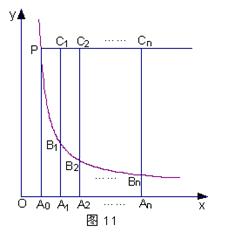
6.如图，直线
和双曲线
相交于点P，过P点作PA0垂直x轴，垂足A0，x轴上的点A0、A1、A2、……、An的横坐标是连续整数。过点A1、A2、……、An分别作x轴的垂线，与双曲线(x > 0)及直线分别交于点B1、B2、……、Bn、C1、C2、……、Cn.
⑴求A0点坐标；
⑵求
及
的值；
⑶试猜想
的值(直接写答案)
7．已知抛物线y=ax2(a>0)上有两点A、B，其横坐标分别为－1，2，请探求关于a的取值情况，△ABO可能是直角三角形吗？不能，说明理由；能是直角三角形，写出探求过程。
参考答案
一、1、B 2、A 3、B 4、C 5、B 6、D 7、B 8、B 9、A 10、A 11、D 12、C 13、D
二、1、4； 2、（-1，2）； 3、-2，一、二、四； 4、-2；5、y=2x+2； 6、（-4，-4）； 7、y=2x2+8x+11 ； 8、
。
三、1.(1)y1=15+0.3x (x≥0)
y2=0.6x (x≥0)
(2)如下图:
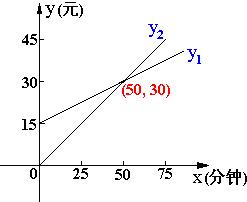
(3)由图像知:
当一个月通话时间大于50分钟时, 甲种业务更优惠
【说明: 用方程或不等式求解进行分类讨论也可】
2、⑴若商店经营该商品不降价，则一天可获利润100×（100-80）＝2000（元）
⑵ ①依题意得：
（100-80-x）（100+10x）＝2160
即x
-10x+16=0
解得：x
=2,x
=8
经检验：x=2,x=8都是方程的解，且符合题意.
答：商店经营该商品一天要获利润2160元，则每件商品应降价2元或8元.
②依题意得：y=（100-80-x）（100+10x）
∴y=
-10x+100x+2000=-10(x-5)+2250
画草图（略）
观察图像可得：当2≤x≤8时，y≥2160
∴当2≤x≤8时，商店所获利润不少于2160元．
3、(1)依题意得
鸡场面积y=－
∵y=－
x2+
x=
(x2－50x)
=－(x－25)2+
,
∴当x=25时，y最大=,
即鸡场的长度为25 m时，其面积最大为m2.
(2)如中间有几道隔墙，则隔墙长为
m.
∴y=·x=－
x2+
x
=－(x2－50x) =－(x－25)2+
,
当x=25时，y最大=,
即鸡场的长度为25 m时，鸡场面积为 m2.
结论：无论鸡场中间有多少道篱笆隔墙，要使鸡场面积最大，其长都是25 m.
4、（1）∵M（1，－2），N（－1，6）在二次函数y = x2+bx+c的图象上，
∴
解得
二次函数的关系式为y = x2－4x+1。
（2）Rt△ABC中，AB = 3，BC = 5，∴AC = 4，
解得
∵A（1，0），∴点C落在抛物线上时，△ABC向右平移
个单位。
5、
解:⑴
⑵（法1）设这条抛物线的函数解析式 为:
∵抛物线过O(0,0)
∴
解得
∴这条抛物线的函数解析式为:
即
.
（法2）设这条抛物线的函数解析式 为:
∵抛物线过O(0,0), 三点，
∴
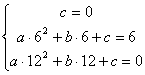解得：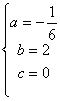
∴这条抛物线的函数解析式为:.
⑶设点A的坐标为
∴OB=m，AB=DC=
根据抛物线的轴对称,可得:
∴
即AD=12－2m
∴
＝AB+AD+DC=
=
=
∴当m=3，即OB=3米时，
三根木杆长度之和的最大值为15米。
6、解： (1)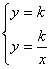
解得x=1，∴点A 0坐标为(1，0)
（2）由于A0、A1、A2点的横坐标为连续整数，
∴A1、A2点的坐标为(2，0)、(3，0)
∴
，
.
∴
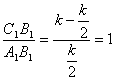
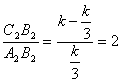
(3) 
7、如下图
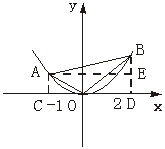
A(－1，a),B(2，4a).
若∠AOB=90°。
(1)∴△ACO∽△ODB,
,
∴4a2=2,a2=
,a=±
∵a>0,∴当a=
时，∠AOB=90°。
(2)使∠BAO=90°，过A作AE⊥BD于E，则AE=3，BE=3a.
∵OB2=AB2+OA2, OA2=AC2+OC2=a2+1,
OB2=OD2+BD2=16a2+4, AB2=9+9a2。
∴16a2+4=9+9a2+a2+1。
a2=1.∵a>0,∴a=1。
当a=1时，∠OAB=90°，即△ABO为直角三角形。