中考数学总复习专题训练（五)
（统计与概率）
考试时间：120分钟 满分150分
一、选择题（每小题4分，共24分）
1. 六个学生进行投篮比赛,投进的个数分别为2、3、10、5、13、3,
这六个数的中位数为（ ）。
Ａ．3 Ｂ．4 Ｃ．5 Ｄ．6
2. 下列事件中,为必然事件是（ ）。
Ａ．打开电视机，正在播广告。
Ｂ．从一个只装有白球的缸里摸出一个球，摸出的球是白球。
Ｃ．从一定高度落下的图钉，落地后钉尖朝上。
Ｄ．今年5月1日，泉州市的天气一定是晴天。
3. 下列调查方式合适的是（ ）。
Ａ．了解炮弹的杀伤力,采用普查的方式。
Ｂ．了解全国中学生的睡眠状况,采用普查的方式。
Ｃ．了解人们保护水资源的意识,采用抽样调查的方式。
Ｄ．对载人航天器“神舟六号”零部件的检查,采用抽样调查的方式。
4. 中央电视台“幸运52”栏目中的“百宝箱”互动环节，是一种竞猜游戏，游戏规则如下：在20个商标中，有5个商标牌的背面注明了一定的奖金额，其余商标的背面是一张苦脸，若翻到它就不得奖.参加这个游戏的观众有三次翻牌的机会.某观众前两次翻牌均得若干奖金，如果翻过的牌不能再翻，那么这位观众第三次翻牌获奖的概率是（ ）。
Ａ．
Ｂ．
Ｃ．
Ｄ．
5. 一位卖“运动鞋”的经销商到一所学校对9位学生的鞋号进行了抽样调查,其号码为：24,22,21,24,23,20,24,23,24。经销商最感兴趣的是这组数据中的（ ）。
Ａ．中位数 Ｂ．众数 Ｃ．平均数 Ｄ．方差
6. 如图的转盘被划分成六个相同大小的扇形,并分别标上1,2,3,4,5,6这六个数字,指针停在每个扇形的可能性相等,四位同学各自发表了下述见解：
甲：如果指针前三次都停在3号扇形,下次就一定不会停在3号扇形了。
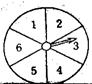乙：只要指针连续转六次,一定会有一次停在6号扇形。
丙：指针停在奇数号扇形的概率和停在偶数号扇形的概率相等。
丁：运气好的时候,只要在转动前默默想好让指针停在6号扇形,
指针停在6号扇形的可能性就会加大。
其中你认为正确的见解有（ ）。
Ａ．1个 Ｂ．2个 Ｃ．3个 Ｄ．4个
二、填空题（每小题4分，共48分）
1. 在200320042005200620072008的数字串中,2的频率是_________。
2. 为了解某校初三年级300名学生的身高状况,从中抽查了50名学生,
所获得的样本容量是______________。
3. 若1000张奖券中有200张可以中奖,则从中任抽1张能中奖的概率为_________。
4. 一射击运动员在一次射击练习中打出的成绩（单位:环）是：7,8,9,8,6,8,10,7,这组数据的众数是_____ ____。
5. 一口袋中放有3只红球和4只黄球,这两种球除颜色外没有任何区别。
随机从口袋中任取一只球,取到黄球的概率是________。
6. 如果一组数据3,x,1,7的平均数是4,则x=__________。
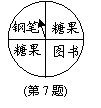
7. 某班的联欢会上,设有一个摇奖节目,奖品为钢笔、图书和糖果,
标于一个转盘的相应区域上（转盘被均匀等分为四个区域，如图），
转盘可以自由转动。参与者转动转盘，当转盘停止时，指针落在哪一区域，就获得哪种奖品,则获得钢笔的概率为____________。
8. 某学生在一次考试中,语文、数学、英语三门学科的平均成绩是80分,物理、化学两门学科的平均成绩为85分,则该学生这五门学科的平均成绩是___________分。
9. 对甲、乙两台机床生产的零件进行抽样测量,其平均数、方差计算结果如下：机床甲:
=10，
=0.02；机床乙：
=10，
=0.06，
由此可知：________（填甲或乙）机床性能好。
10. 掷一枚均匀的硬币两次,两次正面都朝上的概率是__________。
三、解答下列各题（第1题8分，其余每小题10分，共78分）
1.一个口袋中有10个红球和若干个白球，请通过以下实验估计口袋中白球的个数：从口袋中随机摸出一球，记下其颜色，再把它放回口袋中，不断重复上述过程．实验中总共摸了200次，其中有50次摸到红球。
2.甲、乙两位同学五次数学测验成绩如下表：
| 测验(次) | 1 | 2 | 3 | 4 | 5 | 平均数 | 方差 |
| 甲(分) | 75 | 90 | 96 | 83 | 81 | ||
| 乙(分) | 86 | 70 | 90 | 95 | 84 |
请你在表中的空白处填上适当的数，用学到的统计知识对两位同学的成绩进行分析，并写出一条合理化建议．
3.四张大小、质地均相同的卡片上分别标有数字1，2，3，4，现将标有数字的一面朝下扣在桌子上，从中随机抽取一张（不放回），再从桌子上剩下的3张中随机抽取第二张.
（1）用画树状图或列表的方法,列出前后两次抽得的卡片上所标数字的所有可能情况;
（2）计算抽得的两张卡片上的数字之积为奇数的概率是多少？
4.某单位对应聘者甲、乙、丙进行面试,并从专业知识、工作经验、仪表形象三方面给应聘者打分,每一方面满分20分，最后的打分情况如下表所示：
| 甲 | 乙 | 丙 | |
| 专业知识 | 14 | 18 | 16 |
| 工作经验 | 17 | 15 | 15 |
| 仪表形象 | 12 | 11 | 14 |
（1）如果专业知识、工作经验、仪表形象三个方面的重要性之比为10∶7∶3，那么作为人事主管，你应该录用哪一位应聘者？为什么？
（2）在（1）的条件下，你对落聘者有何建议？
5.有一个抛两枚硬币的游戏，规则是：若出现两个正面，则甲赢；若出现一正一反，则乙赢；若出现两个反面，则甲、乙都不赢。
(1)这个游戏是否公平？请说明理由；
(2)如果你认为这个游戏不公平，那么请你改变游戏规则，设计一个公平的游戏；如果你认为这个游戏公平，那么请你改变游戏规则，设计一个不公平的游戏。
6.学习了统计知识后,小刚就本班同学的上学方式进行了一次调查统计.图(1)和图(2)是他通过采集数据后,绘制的两幅不完整的统计图。请你根据图中提供的信息,解答以下问题:
(1)求该班共有多少名学生?
(2)在图（1）中,将表示“步行”的部分补充完整。
(3)在扇形统计图中，计算出“骑车”部分所对应的圆心角的度数。
(4)如果全年级共500名同学,请你估算全年级步行上学的学生人数。
 |
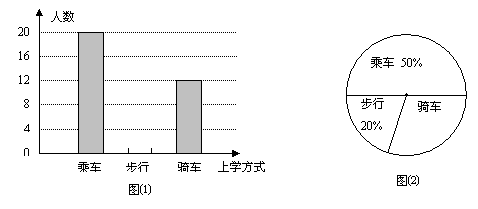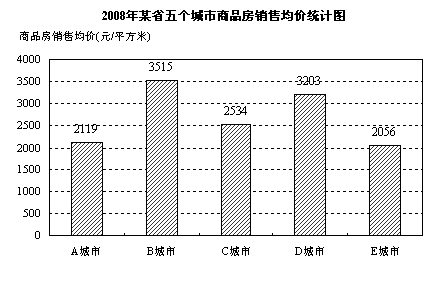
7.某同学根据2008年某省五个城市商品房销售均价（即销售平均价）的数据，绘制了如下统计图：
（1）这五个城市2008年商品房销售均价的中位数、极差分别是多少？
（2）若2006年A城市的商品房销售均价为1600元/平方米，试估计A城市从2006年到2008年商品房销售均价的年平均增长率约是多少（要求误差小于1%）？
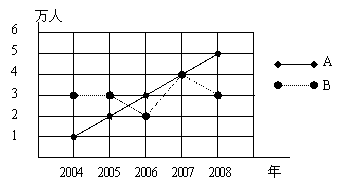
8.如图所示,A、B两个旅游点从2004年至2008年“五、一”的旅游人数变化情况分 别用实线和虚线表示,根据图中所示解答以下问题：
（1）B旅游点的旅游人数相对上一年,增长最快的是哪一年？
（2）求A、B两个旅游点从2004到2008年旅游人数的平均数和方差,并从平均数和方差的角度,用一句话对这两个旅游点的情况进行评价；
（3）A旅游点现在的门票价格为每人80元,为保护旅游点环境和游客的安全,A旅游点的最佳接待人数为4万人,为控制游客数量，A旅游点决定提高门票价格。已知门票价格x (元)与游客人数y（万人）满足函数关系
。若要使A旅游点的游客人数不超过4万人,则门票价格至少应提高多少？
 |
中考数学总复习专题训练（五)参考答案
一、1.B, 2.B, 3.C, 4. B, 5.B, 6.A.
二、1.
, 2.50, 3.0.2, 4.8, 5.
, 6.5, 7.
, 8.82, 9.甲, 10. .
三、1.设口袋中有
个白球，
由题意，得
， 解得=30． 口袋中约有30个白球．
2．甲：8 5，5 3．2．乙：8 5，7 0．4．
建议例如:从上述数据可以看出，乙同学的数学成绩不够稳定，波动较大，希望乙同学在学习上补缺补漏，加强能力训练． www.1230.org 初中
 |
3.（1）
（2）P（积为奇数）=
4.（1）甲得分：14×
＋17×
＋12×
=
乙得分：18×＋15×＋11×=
丙得分：16×＋15×＋14×=
∴应录用乙
（2）建议例如:对甲而言，应加强专业知识的学习，同时要注意自己的仪表形象．对丙而言，三方面都要努力,重点在专业知识和工作经验 .
5.（1）∵P(出现两个正面)=，P(出现一正一反)=
两者概率不同， ∴这个游戏不公平.(2)略. www.1230.org 初中数学资源网 收集整理
（2）∵P(和大于7)=
< P(和小于或等于7)=
∴这个游戏对双方不公平
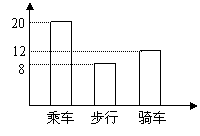6.（1）40人
（2）见右图
（3）圆心角度数=
=108º
（4）估计该年级步行人数=500×20%=100
7. （1）中位数是2534（元/平方米）；
极差是3515－2056＝1459（元/平方米）．
（2）设A城市2006年到2008年的年平均增长率为x，由题意，得:
1600(1＋x)2＝2119．
(1+x)2＝1.324375，
∵x＞0，∴1+ x＞0，
∴1+x ≈1.151 x ≈0.15
即平均增长率约为15%
8. (1)B旅游点的旅游人数相对上一年增长最快的是2007年。
(2)
＝
＝3（万元） 
＝
＝3（万元）
＝
[(-2)
＋(-1)＋0＋1＋2]＝2 
＝[0＋0＋(-1)＋1＋0]＝
从2004至2008年，A、B两个旅游点平均每年的旅游人数均为3万人，但A旅游点较B旅游点的旅游人数波动大。
(3)由题意，得 ５－
≤４ 解得x≥100 100-80＝20
则A旅游点的门票至少要提高20元。