《相似形》提高试题
（一）选择题：（每题2分，共24分）
1．梯形两底分别为m、n，过梯形的对角线的交点，引平行于底边的直线被两腰所截得的线段长为………………………………………………………………………（ ）
（A）
（B）
（C）
（D）
【提示】设所要求的线段长为x，则有
＝1．
【答案】B．
2．如图，在正三角形ABC中，D，E分别在AC，AB上，且
＝
，AE＝BE，则有………………………………………………………………………………………（ ）
（A）△AED∽△BED （B）△AED∽△CBD
（C）△AED∽△ABD （D）△BAD∽△BCD
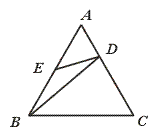
【提示】AE＝
BC，AD＝CD．
【答案】B．
3．P是Rt△ABC斜边BC上异于B、C的一点，过点P作直线截△ABC，使截得的三角形与△ABC相似，满足这样条件的直线共有……………………………………（ ）
（A）1条 （B）2条 （C）3条 （D）4条
【提示】所截得的三角形为直角三角形，过P点分别作△ABC三边的垂线，可作3条．
【答案】C．
4．如图，∠ABD＝∠ACD，图中相似三角形的对数是……………………………（ ）
（A）2 （B）3 （C）4 （D）5
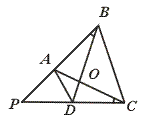
【提示】△AOB∽△COD，△AOD∽△BOC，△PAC∽PDB，△PAD∽△PCB．
【答案】C．
5．如图，ABCD是正方形，E是CD的中点，P是BC边上的一点，下列条件中，不能推出△ABP与△ECP相似的是……………………………………………………（ ）
（A）∠APB＝∠EPC （B）∠APE＝90°
（C）P是BC的中点 （D）BP︰BC＝2︰3
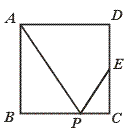
【提示】当P是BC的中点时，△EPC为等腰直角三角形．
【答案】C．
6．如图，△ABC中，AD⊥BC于D，且有下列条件：
（1）∠B＋∠DAC＝90°；（2）∠B＝∠DAC；
（3）
＝
； （4）AB2＝BD·BC
其中一定能够判定△ABC是直角三角形的共有………………………………（ ）
（A）3个 （B）2个 （C）1个 （D）0个
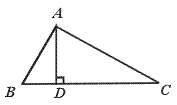
【提示】∵ ∠B＝∠DAC，
∴ （1）错，（2）对．
【答案】A．
7．如图，将△ADE绕正方形ABCD顶点A顺时针旋转90°，得△ABF，连结EF交AB于H，则下列结论中错误的是………………………………………………（ ）
（A）AE⊥AF （B）EF︰AF＝
︰1
（C）AF2＝FH·FE （D）FB︰FC＝HB︰EC
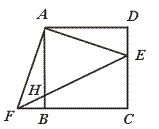
【提示】先检验A、B、D的正确性．
【答案】C．
8．如图，在矩形ABCD中，点E是AD上任意一点，则有…………………（ ）
（A）△ABE的周长＋△CDE的周长＝△BCE的周长
（B）△ABE的面积＋△CDE的面积＝△BCE的面积
（C）△ABE∽△DEC
（D）△ABE∽△EBC
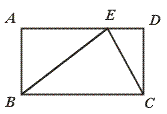
【提示】作EF⊥BC，垂足为F．
【答案】B．
9．如图，在□ABCD中，E为AD上一点，DE︰CE＝2︰3，连结AE、BE、BD，且AE、BD交于点F，则S△DEF︰S△EBF︰S△ABF等于……………………………（ ）
（A）4︰10︰25 （B）4︰9︰25 （C）2︰3︰5 （D）2︰5︰25
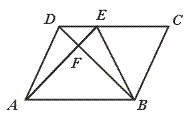
【提示】△DEF∽△ABF，S△DEF︰S△BEF＝DF︰BF＝DE︰AB．
【答案】A．
10．如图，直线a∥b，AF︰FB＝3︰5，BC︰CD＝3︰1，则AE︰EC为（ ）．
（A）5︰12 （B）9︰5 （C）12︰5 （D）3︰2
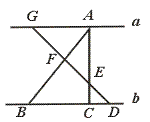
【提示】
＝
＝
．
【答案】C．
11．如图，在△ABC中，M是AC边中点，E是AB上一点，且AE＝
AB，连结EM并延长，交BC的延长线于D，此时BC︰CD为……………………………（ ）
（A）2︰1 （B）3︰2 （C）3︰1 （D）5︰2
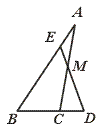
【提示】过C点作CF∥BA交ED于F点，则AE＝CF．
【答案】A．
12．如图，矩形纸片ABCD的长AD＝9 cm，宽AB＝3 cm，将其折叠，使点D与点B重合，那么折叠后DE的长和折痕EF的长分别为………………………………（ ）
（A）4 cm、
cm （B）5 cm、 cm
（C）4 cm、2
cm （D）5 cm、2 cm
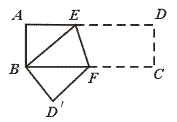
【提示】连结BD交EF于O点，则EF＝2FO，EF⊥BD．由Rt△BOF∽Rt△BCD，
可得
＝
，求出OF的长．又 DE＞AD．
【答案】B．
（二）填空题：（每题2分，共20分）
13．已知线段a＝6 cm，b＝2 cm，则a、b、a＋b的第四比例项是_____cm，a＋b与
a－b的比例中项是_____cm．
【提示】6︰2＝8︰x；y2＝8×4．
【答案】
；4．
14．若
＝
＝
＝－m2，则m＝______．
【提示】分a＋b＋c≠0和a＋b＋c＝0两种情况．
【答案】±1．
15．如图，在△ABC中，AB＝AC＝27，D在AC上，且BD＝BC＝18，DE∥BC交AB于E，则DE＝_______．
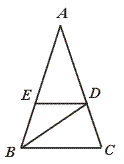
【提示】由△ABC∽△BCD，列出比例式，求出CD，再用△ABC∽△AED．
【答案】10．
16．如图，□ABCD中，E是AB中点，F在AD上，且AF＝FD，EF交AC于G，则AG︰AC＝______．
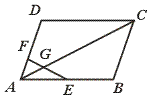
【提示】延长FE交CB延长线于H点，则AF＝BH，考虑△AFG∽△CHG．
【答案】1︰5．
17．如图，AB∥CD，图中共有____对相似三角形．
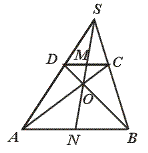
【提示】分“
”类和“
”类两类．
【答案】6对．
18．如图，已知△ABC，P是AB上一点，连结CP，要使△ACP∽△ABC，只需添加条件______（只要写出一种合适的条件）．
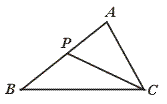
【提示】∵ ∠A为公共角，
∴ 考虑∠A的两边或其他内角相等．
【答案】∠B＝∠ACP，或∠ACB＝∠APC，或AC2＝AP·AB．
19．如图，AD是△ABC的角平分线，DE∥AC，EF∥BC，AB＝15，AF＝4，则DE的长等于________．
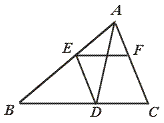
【提示】DE＝AE，CF＝DE，并考虑
＝
．
【答案】6．
20．如图，△ABC中，AB＝AC，AD⊥BC于D，AE＝EC，AD＝18，BE＝15，则
△ABC的面积是______．
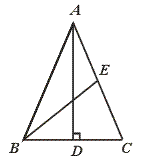
【提示】作EF∥BC交AD于F．设BE交AD于O点，先求出OD长和OB长，最后用勾股定理求出BD的长．
【答案】144．
21．如图，直角梯形ABCD中，AD∥BC，AC⊥AB，AD＝8，BC＝10，则梯形ABCD面积是_________．
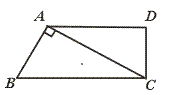
【提示】作AE∥DC交BC于E点，由Rt△ABE∽Rt△CBA，依次算出BE、AB的长，最后求出AE的长，即可求出梯形面积．
【答案】36．
22．如图，已知AD∥EF∥BC，且AE＝2EB，AD＝8 cm，AD＝8 cm，BC＝14 cm，
则S梯形AEFD︰S梯形BCFE＝____________．
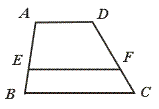
【提示】延长EA，与CD的延长线交于P点，则△APD∽△EPF∽△BPC．
【答案】
．
（三）画图题：（4分）
23．方格纸中，每个小格的顶点叫做格点，以格点连线为边的三角形叫做格点三角形．请你在图示的10×10的方格纸中，画出两个相似但不全等的格点三角形，并加以证明（要求所画三角形是钝角三角形，并标明相应字母）．
【提示】先任意画一个格点钝角三角形，然后三边都扩大相同的倍数，画出另一个格点钝角三角形．
（四）证明题：（每题7分，共28分）
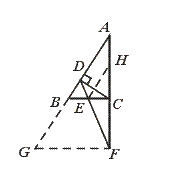
24．如图，△ABC中，CD⊥AB于D，E为BC中点，延长AC、DE相交于点F，
求证
＝
．
【提示】过F点作FG∥CB，只需再证GF＝DF．
【答案】方法一：作FG∥BC交AB延长线于点G．
∵ BC∥GF，
∴ ＝
．
又 ∠BDC＝90°，BE＝EC，
∴ BE＝DE．
∵ BE∥GF，
∴ 
＝
＝1．
∴ DF＝GF．
∴ ＝．
方法二：作EH∥AB交AC于点H．
∵ ＝
，＝
，
∠BDC＝90°，BE＝EC，
∴ BE＝DE．
∴ ＝．
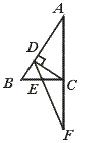
25．如图，在△ABC中，AB＝AC，延长BC至D，使得CD＝BC，CE⊥BD交AD于E，连结BE交AC于F，求证AF＝FC．
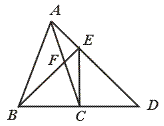
【提示】先证△BCF∽△DBA，再证
＝．
【答案】∵ BC＝CD，EC⊥BD，
∴ BE＝DE，∠FBC＝∠D．
又 AB＝AC，
∴ ∠BCF＝∠DBA．
∴ ∠BCF∽△DBA．
∴ 
＝
．
又 BD＝2BC，AB＝AC，
∴ ＝
＝．
∴ FC＝AC．
因此 AF＝FC．
26．已知：如图，F是四边形ABCD对角线AC上一点，EF∥BC，FG∥AD．
求证：＋
＝1．
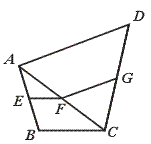
【提示】利用AC＝AF＋FC．
【答案】∵ EF∥BC，FG∥AD，
∴ ＝，＝
．
∴ ＋＝＋＝
＝1．
27．如图，BD、CE分别是△ABC的两边上的高，过D作DG⊥BC于G，分别交CE及BA的延长线于F、H，求证：
（1）DG2＝BG·CG；（2）BG·CG＝GF·GH．
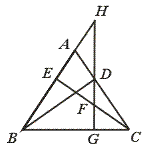
【提示】（1）证△BCG∽△DCG；（2）证Rt△HBG∽Rt△CFG．
【答案】（1）DG为Rt△BCD斜边上的高，
∴ Rt△BDG∽Rt△DCG．
∴ 
＝
，即DG2＝BG·CG．
（2）∵ DG⊥BC，
∴ ∠ABC＋∠H＝90°，CE⊥AB．
∴ ∠ABC＋∠ECB＝90°．
∴ ∠ABC＋∠H＝∠ABC＋∠ECB．
∴ ∠H＝∠ECB．
又 ∠HGB＝∠FGC＝90°，
∴ Rt△HBG∽Rt△CFG．
∴ 
＝
，
∴ BG·GC＝GF·GH．
（五）解答题：（每题8分，共24分）
28．如图，∠ABC＝∠CDB＝90°，AC＝a，BC＝b．
（1）当BD与a、b之间满足怎样的关系时，△ABC∽△CDB？
（2）过A作BD的垂线，与DB的延长线交于点E，若△ABC∽△CDB．
求证四边形AEDC为矩形（自己完成图形）．
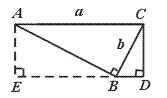
【提示】利用三角形相似，推出BD＝
．
【答案】（1）∵ ∠ABC＝∠CDB＝90°，
∴ 当＝
时，△ABC∽△CDB．
即 
＝
．
∴ BD＝．
即当BD＝时，△ABC∽△CDB．
∵ △ABC∽△CDB，
∴ ∠ACB＝∠CBD．
∴ AC∥ED．
又 ∠D＝90°，
∴ ∠ACD＝90°．
∴ ∠E＝90°．
∴ 四边形AEDC为矩形．
29．如图，在矩形ABCD中，E为AD的中点，EF⊥EC交AB于F，连结FC
（AB＞AE）．
（1）△AEF与△EFC是否相似？若相似，证明你的结论；若不相似，请说明理由；
（2）设
＝k，是否存在这样的k值，使得△AEF∽△BFC，若存在，证明你的结论并求出k的值；若不存在，说明理由．
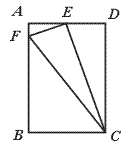
【提示】（1）如图，证明△AFE≌△DGE，证出∠AFE＝∠EFC．
（2）证明∠ECG＝30°，∠BCF＝30°．
【答案】如图，是相似．
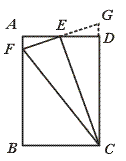
【证明】延长FE，与CD的延长线交于点G．
在Rt△AEF与Rt△DEG中，
∵ E是AD的中点，
∴ AE＝ED．
∵ ∠AEF＝∠DEG，
∴ △AFE≌△DGE．
∴ ∠AFE＝∠DGE．
∴ E为FG的中点．
又 CE⊥FG，
∴ FC＝GC．
∴ ∠CFE＝∠G．
∴ ∠AFE＝∠EFC．
又 △AEF与△EFC均为直角三角形，
∴ △AEF∽△EFC．
① 存在．如果∠BCF＝∠AEF，即k＝＝
时，△AEF∽△BCF．
证明：当＝时，
＝，
∴ ∠ECG＝30°．
∴ ∠ECG＝∠ECF＝∠AEF＝30°．
∴ ∠BCF＝90°－60°＝30°．
又 △AEF和△BCF均为直角三角形，
∴ △AEF∽△BCF．
② 因为EF不平行于BC，
∴ ∠BCF≠∠AFE．
∴ 不存在第二种相似情况．
30．如图，在Rt△ABC中，∠C＝90°，BC＝6 cm，CA＝8 cm，动点P从点C出
发，以每秒2 cm的速度沿CA、AB运动到点B，则从C点出发多少秒时，可使
S△BCP＝S△ABC？
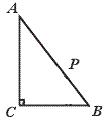
【提示】先求CP，再求DP．
【答案】当点P从点C出发，运动在CA上时，若S△BCP＝S△ABC，则
·CP·BC＝·AC·BC，
∴ CP＝·AC＝2（cm）．
故由点P的运动速度为每秒2 cm，它从C点出发1秒时，有S△BCP＝S△ABC．当点P从点C出发运动到AB上时，如图，可过点P作PD⊥BC于D．
若S△BCP＝S△ABC，则
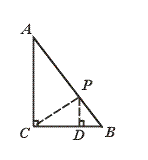
PD·BC＝·AC·BC．
∴ PD＝AC＝2（cm）．
∵ Rt△BAC∽Rt△BPD，
∴ 
＝
．
又 AB＝
＝10，
故 BP＝
＝
，AP＝AB－BP＝10－＝7.5．
也就是说，点P从C出发共行15.5 cm，用去7.75秒，此时S△BCP＝S△ABC．
答：1秒或7.75秒．