中考数学不等式
〖知识点〗
不等式概念，不等式基本性质，不等式的解集，解不等式，不等式组，不等式组的解集，解不等式组，一元一次不等式，一元一次不等式组。
大纲要求
1.理解不等式，不等式的解等概念，会在数轴上表示不等式的解；
2.理解不等式的基本性质，会应用不等式的基本性质进行简单的不等式变形，会解一元一次不等式；
3.理解一元一次不等式组和它的解的概念，会解一元一次不等式组；
4.能应用一元一次不等式（组）的知识分析和解决简单的数学问题和实际问题。
内容分析
一元一次不等式、一元一次不等式组的解法
(1)只含有一个未知数，并且未知数的次数是1，系数不为零的不等式，叫做一元一次不等式．
解一元一次不等式的一般步骤是去分母、去括号、移项、合并同类项和系数化成1．要特别注意，不等式的两边都乘以(或除以)同一个负数，要改变不等号的方向．
(2)解一元一次不等式组的一般步骤是：
(i)先求出这个不等式组中各个一元一次不等式的解集；
(ii)再利用数轴确定各个解集的公共部分，即求出了这个一元一次不等式组的解集．
考查重点与常见题型
考查解一元一次不等式（组）的能力，有关试题多为解答题，也出现在选择题，填空题中。
考查题型
1．下列式子中是一元一次不等式的是（ ）
(A)-2>-5 (B)x2>4 (C)xy>0 (D)–x< -1
2．下列说法正确的是（ ）
（A） 不等式两边都乘以同一个数，不等号的方向不变；
（B） 不等式两边都乘以同一个不为零的数，不等号的方向不变；
（C） 不等式两边都乘以同一个非负数，不等号的方向不变；
（D） 不等式两边都乘以（或除以）同一个正数，不等号的方向不变；
3．对不等式的两边进行变形，使不等号方向改变，可采取的变形方法是（ ）
（A）加上同一个负数 （B）乘以同一个小于零的数
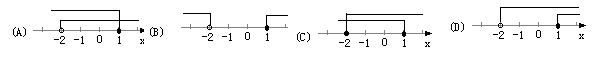
（C）除以同一个不为零的数 （D） 乘以同一个非正数
4．在数轴上表示不等式组
的解，其中正确的是（ ）
5．下列不等式组中，无解的是（ ）
(A) 
(B) 
(C) 
(D) 
6．若a<b 则下列不等式中正确的是（ ）
(A)a-b>0 (B)a+b<0 (C)ac<bc (D)-a> -b
7．解下列不等式（组）
(1)x－<2 + (2)
考点训练：
1． 以知a>b用”>”或”<”连接下列各式；
（1）a-3 ---- b-3, (2)2a ----- 2b, (3)- ----- － (4)4a-3 ---- 4b-3 (5)a-b --- 0
2． 判断题：
(1) 若 a>b 则< ( ) (2) 若a>b 则a>b ( )
(3)若ac >bc 则 a>b ( ) (4)若> 则a>b ( )
3．a,b是已知数，当a>0时，不等式ax+b<0的解集为------------, 当a<0不等式ax+b<0的解集为----------------
4．已知正整数x满足<0 ，则代数式(x－2)1999 － 的值是----------------.
5．解不等式x－≥－1，将解集在数轴上表示出来，且写出它的正整数解
6．解不等式组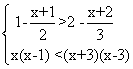
7． x为何值时，代数式－3(x+4)的值是：（1）非负数（2）不大于零
8．已知三角形三边长分别为3，（1－2ａ），8，试求ａ的取值范围。
解题指导：
1． 解不等式1－>，并说明每一步的理由。
2． 比较x2－4x－1与x2－6x＋3的大小。
3． 已知不等式5(x－2)＋8 < 6(x－1)＋7的最小整数解为方程2x－ax=3的解，求代数式4a－的值。
4． 求不等式组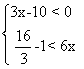
的整数解
5． 已知方程组
的解为正数，求（1）a的取值范围。
（2）化简4a+5－a-4
＊6．ａ、ｂ为任意实数。解关于ｘ的不等式ａ（ｘ＋ｂ2）＞ｂ（ｘ＋ａ2）
独立训练：
1．用不等式表示：x的与5的差小于1为________
2.不等式5x－17≤0的正整数解是-------------_;不等式组
的解集是--------------
3．代数式1-的值不大于的值，那么的取值范围是_____________.
 |  |  |  | ||||
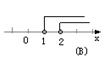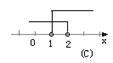4．不等式组
的解集在数轴上的表示是（ ）
5．如果0<x<1则,x,x2 这三个数的大小关系可表示为（ ）
(A)x< < x2 (B)x <x2< (C) <x<x2 (D) x2<x<
6．如果方程(a-2)x= -3的解是正数，那么（ ）
(A)a>0 (B)a<0 (C)a<2 (D)a>2
7．已知不等式组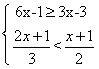
的整数解满足方程3(x+a)－5a= －2，求代数式633(a2+)的值。
8．解不等式－1≤< 4
9．不等式
组的解5<x<22是求a,b的值
10．解不等式 3 <2x+1 < 5 11.解不等式－x2－3x>