初中数学毕业生学业考试仿真模拟试卷
数 学 试 题（一）
考生注意：
1.全卷试题共五大题25小题，卷面满分120分，考试时间120分钟；
2.本试卷分为两卷，解答第Ⅰ卷（1—2页）时请将解答结果填写在第Ⅱ卷（3—8页）上指定的位置，否则答案无效；交卷时只交第Ⅱ卷；
3.做本卷试题可使用科学计算器；
以下公式共参考：
二次函数y=ax2+bx+c（a≠0）图象的顶点坐标是（- ，）；弧长l=πR.
第Ⅰ卷（选择题、填空题 共45分）
一、选择题.（本大题满分30分，共10小题，每小题3分）
下列各小题都给出了四个选项，其中只有一个符合题目要求，请把符合题目要求的选项前的字母代号填写在第Ⅱ卷上指定的位置.
1.温度上升5℃记为+5℃，那么下降3℃应记为（ ）
A.+3℃ B.-3℃ C.+5℃ D.-5℃
2.正方形具有但矩形不一定具有的性质是（ ）
A.对角线互相垂直 B.对角线相等
C.对角线互相平分 D.对边平行且相等
3.两个不透明的袋中都各装有一个红球和一个黄球两个球，它们除了颜色外都相同.现随机从两个袋中各摸出一个球，两个球的颜色是一红一黄的概率是（ ）
A. B. C. D.
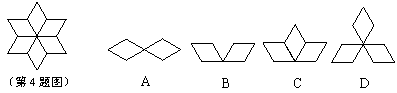4.如下左图所示的图案是由六个全等的菱形拼成的，它也可以看作是以一个图案为“基本图案”，通过旋转得到的.以下图案中，不能作为“基本图案”的一个是（ ）
5.计算式子22·（22）3的结果用幂的形式表示正确的是（ ）
A. 27 B.28 C.210 D.212
6.今测得太阳光线与水平面的夹角是53°，一棵竖直生长的雪松在水平地面上的影长为6米，则这棵雪松的高度h（单位：米）的范围是（ ）
A.2＜h＜3 B. 3＜h＜6 C. 6＜h＜11 D. 11＜h＜15
7.小华在用计算器估算一元二次方程x2-3x+1=0的近似解时，对代数式x2-3x+1进行了代值计算，并列成下表.由此可以判断，一元二次方程x2-3 x+1=0的一个解x的范围是（ ）
A.-1＜x＜-0.5 B.-0.5＜x＜0
C.0＜x＜0.5
D.0.5＜x＜1
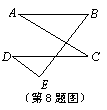
8.如图，AB∥CD，∠A=30°，则∠A+∠B+∠C+∠D+∠E=（ ）
A.240° B.270° C.300° D.360°
| x | -1 | -0.5 | 0 | 0.5 | 1 |
| x2-3 x+1 | 5 | 2.75 | 1 | -0.25 | -1 |
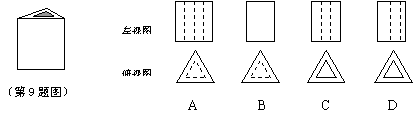9.如下左图，直三棱柱工件的底面是等边三角形，在它的中间有一个直三棱柱空洞，那么这个工件的左视图和俯视图分别是（ ）
 |
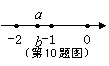10.实数a在数轴上对应点的位置如图所示，下列结论错误的是（ ）
A.∣a∣＞1 B.∣a∣＜ 2 C.∣a-1∣＞2 D.∣a+2∣＞1
二、填空题.（本大题满分15分，共5小题，每小题3分）
请将下列各题的答案填写在第Ⅱ卷上指定的位置.
11.近几年，宜昌市国民经济继续保持强劲增长的势头，财政收入也逐年增加，2006年全市财政总收入突破147亿元，那么数据147亿元用科学记数法表示为 元.
12.一次函数y=kx+2经过点（1，0），则k= .
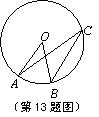
13.如图，点O是⊙O的圆心，点A、B、C在⊙O上，AO∥BC，∠AOB=38°，则∠OAC的度数是 .
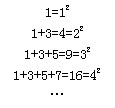14.甲、乙两厂分别生产直径为246mm的标准篮球.从两厂各自生产的篮球中分别随机抽取10个，得到甲厂篮球实际直径的方差是2，乙厂篮球实际直径的标准差S乙=1.96.那么所抽甲厂篮球实际直径的标准差S甲= ，生产质量较稳定的厂是 厂.
15.从1开始，连续奇数相加，它们和的情况如右所示.当连续相加的最后一个奇数是n时，其和1+3+5+…+n= .
初中毕业生学业考试仿真模拟试卷
数 学 试 题（一）
| 题 号 | 一 | 二 | 三 | 四 | 五 | 总 分 |
| 得 分 |
第Ⅱ卷（ 解答题 共75分）
一、选择题答案栏.（本大题满分30分）请将第Ⅰ卷中选择题的答案填写在下表中.
| 得分 | 评卷人 | 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 答案 |
二、填空题答案栏.（本大题满分15分）请将第Ⅰ卷中填空题的答案填写在下表中.
| 得分 | 评卷人 | 题号 | 11 | 12 | 13 | 14 | 15 | ||
| 答案 | |||||||||
| 得分 | 评卷人 |
三、解答题.（本大题满分24分，共4小题，每小题6分）
16.计算： ·（ + ）.
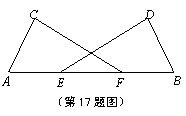
17.如图，已知∠A=∠B，AE=EF=FB，AC=BD.求证：CF=DE.
 |
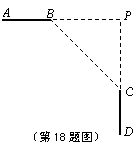
18.如图AB、CD是两条垂直的公路，设计时想在拐弯处用一段圆弧形弯道把它们连接起来（圆弧在B、D两处分别与道路相切），测得BC=100米，∠PBC=45°.
（1）⑴在图中画出圆弧形弯道的示意图（用尺规作图，保留作图痕迹，不写作法与证明）；
（2）计算弯道部分的长度（结果用π表示并保留根号）.
 |
19.据新华网报道，截至2005年底，北京市林木绿化率达到了50.5%，，提前3年实现了2008年林木绿化率50%的目标.北京市现有土地面积约16800平方千米，“十一五”期间，北京市将紧紧围绕“办绿色奥运、建生态城市”总体发展战略，计划到“十一五”期末的2010年，使全市林木绿化率超过53%. 求“十一五”这5年期间，平均每年林木绿化面积至少要达到多少平方千米.
| 得分 | 评卷人 |
四、解答题.（本大题满分21分，共3小题，每小题7分）
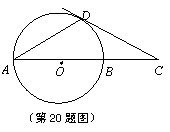
20.如图，⊙O的直径AB=6cm，D为⊙O上一点，∠BAD=30°，过点D的切线交AB的延长线于点C.求∠ADC的度数及AC的长.
 |
21.某养鱼专业户在鱼塘中放有100条红色鲤鱼和其他鱼种若干.为了估计鱼塘中鱼的总重量，鱼主分三次进行了随机抽样捕捞，每次都称出从鱼塘中捕捞出鱼的总重量，记下鱼的总条数和红色鲤鱼的条数，然后将鱼全部放回鱼塘.三次捕捞的记载情况如下表：
（1）请你根据表中的数据，估计鱼塘中鱼的总条数和总重量；
| 项 目 | 第1次 | 第2次 | 第3次 |
| 捕捞鱼的总条数 | 60 | 60 | 80 |
| 捕捞鱼的总重量（千克） | 146 | 151 | 203 |
| 其中红色鲤鱼的条数 | 3 | 4 | 3 |
（2）若红色鲤鱼每千克的平均售价为10元，其他鱼为每千克6元，该养鱼专业户出售完鱼塘中的鱼可创收多少元？
22.在一次探究性活动中，教师提出了以下问题：已知矩形的长和宽分别是1和0.5，是否存在一个矩形，它的周长和面积是已知矩形周长和面积的2倍？
设所求矩形的长和宽分别为x、y.
（1）从周长的角度考虑，写出x、y应满足的函数关系式①；从面积的角度考虑，写出x、y应满足的函数关系式②；
（2）在下面同一坐标系中画出函数①和②的图象；观察所画的图象，你能得出探究的结论吗？为什么？
（3）解决这个探究性的问题，你还有其他的方法吗？试一试.
 |
 |
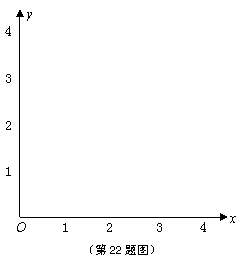| 得分 | 评卷人 |
五、解答题.（本大题满分30分，共3小题，每小题10分）
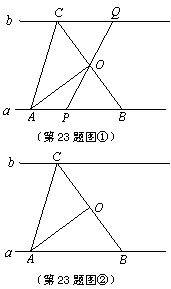
23.如图①，已知直线a∥b，点A、B是a上的点，点C是b上的点，AB=AC=5，BC=6，点O是BC的中点，P是线段AB上一动点（不与B重合），连结PO并延长交b于点Q.
（1）P在运动时，图中变化的线段中有始终保持相等的吗？请你指出其中的一对，并证明你的结论；
（2）当P运动到什么位置时，以O、C、Q为顶点的三角形与△AOC相似？在图②中画出相关图形，标上字母，说明理由，并求出OQ的长.
 |
24.BS超市常年为HY厂代销J型家用微波炉，其销售方式是直接从HY厂按出厂价进货，然后适当加价销售.超市以每台700元的价格销售J型微波炉，可获得40%的利润.2007年元旦来临，厂家和超市为扩大销量、增加利润，决定在元旦假期联合进行降价、让利促销活动.超市对过去J型微波炉的市场销售情况进行了调查：若按原价销售，平均每天可销售10台；若每台降价20元，平均每天可多销4台.厂家对超市承诺：在元旦促销期间销售的J型微波炉的批发价每台优惠20元；对多销的部分，厂家每台再让利50元.
（1）2007年元旦前，BS超市销售一台J型微波炉可获利多少元？
（2）经统计，仅元旦假期三天中，通过降价销售及厂家让利，BS超市销售J型微波炉共获得利润13800元，HY厂也从中获得了丰厚的利润，平均每天的销售收入比BS超市获得的总利润还要多.请你计算元旦期间SB超市确定的J型微波炉的销售单价.
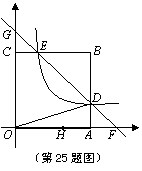
25. 如图，边长为a的正方形OABC与双曲线在第一象限的图象交于D、E两点，S△OAD=；过D、E两点的直线分别交坐标轴于点F、G，过F、G两点的抛物线y=x2+mx+n与x轴相交于另一点H.
⑴求双曲线的解析式；
⑵是否存在这样的a值，使直线AB为抛物线y=x2+mx+n的对称轴？若存在，求出a的
值；若不存在，说明理由；
⑶若OH：HF=2：3，求抛物线y=x2+mx+n的顶点坐标.
 |
参 考 答 案
一、选择题.
1.B；2.A；3.C；4.B；5.B；6.C；7.C；8.A；9.D；10.D.
二、填空题.
11.1.47×1010；12.-2；13.19°；14.或1.41；15.（）2.
三、解答题.
16.a；17.略；18.（1）略，（2）25π米；19.84平方千米.
四、解答题.
20.∠ADC=120°；AC=9；21.（1）2000条，5000千克，（2）31000元；
22.（1）①y=-x+3 ，②y=（2分）；（2）画图象略，结论：存在这样的矩形，它的周长和面积是已知矩形周长和面积的2倍，因为两函数的图象有两个交点，说明同时满足两个函
数关系式的x、y的值存在，且有两对；（3）解决这个问题，还可以看方程组 是否有
解，解这个方程组得：x1=，y1=；或x2=，y2=.即满足条件的矩形的长和宽分别是：和或和.
五、解答题.
23.（1）图中变化的线段中有始终保持相等的，如OP=OQ（或BP=CQ）.证明如下：
∵a∥b，∴∠OBP=∠OCQ，又∵∠POB=∠QOC，BO=CO，∴△POB≌△QOC（ASA），
∴OP=OQ（或BP=CQ）；
（2）∵AB=AC，O是BC的中点，∴AO⊥BC，由勾股定理可求得AO=4；
情况①：当PQ⊥a时，△OQC∽△AOC，理由如下：
∵a∥b，∴∠OCQ=∠OBA，∵AB=AC，∴∠OBA=∠OCA，∴∠OCQ=∠OCA，
∵∠OQC=∠AOC=90°，∴△OQC∽△AOC，
∴CO：AC=OQ：AO，即3：5=OQ：4，∴OQ=；
情况②：当P与A重合时，△QOC≌△AOC，因而△QOC∽△AOC，理由如下：
∵∠OCQ=∠OCA（已证），∠COQ=∠COA=90°，CO=CO，
∴△QOC≌△AOC，因而△QOC∽△AOC，∴OQ=AO=4.
24. （1）设BS超市销售一台J型微波炉可获利x元，依据题意可列方程为：
=40%，解得：x=200（元），进价为：700-200=500（元）；
（2）设元旦期间J型微波炉每台降价20y元，
列方程为：（200-20y）（10+4y）+20×（10+4y）+50×4y=13800÷3
整理得：y2-11y+30=0，解方程得：y=5或y=6，
当y=5时，厂家平均每天的销售收入：（500-20）×（10+4y）-50×4y=13400（元），
当y=6时，厂家平均每天的销售收入：（500-20）×（10+4y）-50×4y=15120（元），
∵13400＜13800＜15120，∴y=5不符合题意，舍去，∴y=6，
元旦期间超市确定的J型微波炉的销售单价为：700-20 y=580（元），答：（略）.
25.（1）设双曲线的解析式为：y=，由S△OAD=可求得k=1，∴双曲线的解析式为：y=；
（2）可求得点D、E的坐标分别为（a，）和（，a），过D、E两点的直线方程为：
x+y=，当x=0时，y=；当y=0时，x=，
所以点F、G的坐标分别为：（，0），（0，），
将两点坐标代入y=x2+mx+n解得：m=---1，n=，
所以，求抛物线的解析式为y=x2-（+1）x + .
假设抛物线的对称轴是直线AB，则有+1=2a，解得a =；
因为a是正方形的边长，所以a＞0，所以满足条件的a的值只有一个，即a =；
（3）可求得抛物线与x轴的另一个交点H的坐标为（1，0），若OH：HF=2：3，
即1：（-1）=2：3，解得a =2或a =（不合题意，舍去）.
当a =2时，抛物线的解析式为y=x2-x+，顶点坐标为（，-）.