初中数学毕业生学业考试仿真模拟试卷
数 学 试 题（二）
考生注意：
1.全卷试题共五大题25小题，卷面满分120分，考试时间120分钟；
2.本试卷分为两卷，解答第Ⅰ卷（1—2页）时请将解答结果填写在第Ⅱ卷（3—8页）上指定的位置，否则答案无效；交卷时只交第Ⅱ卷；
3.做本卷试题可使用科学计算器；
以下公式共参考：
二次函数y=ax2+bx+c(a≠0)图象的顶点坐标是
；扇形面积
=
lr.
第Ⅰ卷 （选择题、填空题 共45分）
一、选择题.（本大题共10个小题，每小题3分，共30分）
在每小题给出的四个选项中，只有一项是符合题目要求的，请将符合要求的选项前面的字母代号填写在第Ⅱ卷上指定的位置。
01．-的倒数是（ ）
A. -2 B. 2 C.- D.
02．如图所示，右面水杯的俯视图是（ ）
03．下列事件：(1)2007年中考那天会下雨；(2)随机掷一枚硬币，正面朝上；(3)13名同学中，有两人出生的生肖相同；(4)2008年奥运会在北京举行。其中不确定事件有（ ）
A.1个 B.2个 C.3个 D.4个
04．下列计算中，正确的是（ ）
A.
B.
C.
D.
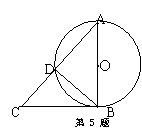
05．如图，在⊙O中，AB是⊙O的直径，AD为弦，过点B的切线
与AD的延长线交于点C，且AD=DC，则∠BAD=（ ）
A. 30° B. 45° C. 60° D. 无法确定
06．夷陵广场占地面积约为55200米2，它的面积与本班教室面积
的倍数关系，下列最接近的是( )
A.200倍 B.400倍 C.500倍
D.700倍
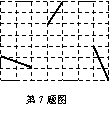
07．如图，将网格中的三条线段沿网格线平移后组成一个首尾相接
的三角形，至少需要移动（ ）
Ａ． 8格 Ｂ．9格 Ｃ．11格 Ｄ．12格
08．某课外兴趣小组为了解所在地区老年人的健康状况，分别作了四种不同的抽样调查．你认为抽样比较合理的是（ ）
A．在宜昌和平公园调查了20名老年人的健康状况
B．在人民中心医院调查了20名老年人的健康状况
C．在我的家乡调查了20名邻居老年人的健康状况
D．利用户籍网随机调查了20名老年人的健康状况
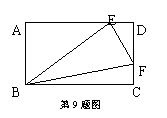
09．如图，在矩形ABCD中，E在AD上，EF⊥BE，交CD于F，
连接BF，则图中与△ABE一定相似的三角形是（ ）
A．△EFB B．△DEF C．△CFB D．△EFB和△DEF
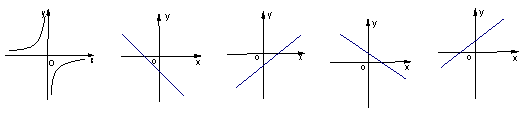10．函数y=(k≠0)的图象如下左图所示，那么函数y=kx-k的图象大致是( ).
A B C D
二、填空题.（本大题共5小题，每小题3分，共15分）
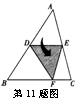
11．如图，D、E为AB、AC的中点，将△ADE沿线段DE折叠，使点A落在点F处，若∠B=500，则∠BDF= .
12．如图，四边形
中，
，要使四边形为平行四边形，则应添加的条件是
（添加一个条件即可）．
 | |||||
 | |||||
 | |||||
13．不透明的袋中装有红球和白球共10个，它们除颜色外都相同.已知从袋中随机摸出一个球是红球的概率是，那么袋中有白球 个.
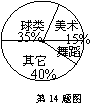
14．如图是实验中学九年级学生参加课外活动人数的扇形统计图，若参加舞蹈类的学生有36人，则参加球类活动的学生人数有 人.
15．下图是用火柴搭成的“金鱼”图形，按此方法搭n 条“金鱼”需要火柴__________根 (用含n的代数式表示).
初中毕业生学业考试仿真模拟试卷
数 学 试 题（二）
| 题 号 | 一 | 二 | 三 | 四 | 五 | 总 分 |
| 得 分 |
第Ⅱ卷（解答题 共75分）
一、选择题答案栏.（本大题满分30分）请将第Ⅰ卷中选择题的答案填写在下表中.
| 得分 | 评卷人 | 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 答案 |
二、填空题答案栏.（本大题满分15分）请将第Ⅰ卷中填空题的答案填写在下表中.
| 得分 | 评卷人 | 题号 | 11 | 12 | 13 | 14 | 15 | ||
| 答案 | |||||||||
三、解答题.（本大题共4小题，每小题6分，共24分）
16.解分式方程：
=1.
17.如图，已知△ABC.
（1）作△ABC的角平分线BD、CE的交点O（尺规作图，保留作图痕迹，不写作法与证明）；
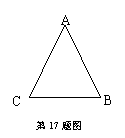（2）在△ABC中，若AC=AB，求证BD=CE.
18.宜昌长江铁路大桥全长2572.73米，共有40个桥跨，其810米的组合跨度在同类型铁路桥中居世界第一.根据设计，建成后通车最低时速为160公里，最高时速可达到250公里.请你估计：全长380米的列车全部通过大桥时间的范围（保留整数秒）.
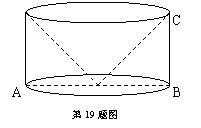
19．如图，是一个由圆柱体材料加工而成的零件，它是以圆柱体的上底面为底面，在其内部“掏取”一个与圆柱体等高的圆锥体而得到的，其底面直径AB=6㎝，高BC=4㎝，求这个零件的表面积（结果保留π）.
 |
四．解答题.（本大题共3小题，每小题7分，共21分）
20．苗苗爸爸买到“2007唱响移动——首届宜昌电视歌手大奖赛”的一张门票，她和哥哥两人都很想去观看，可票只有一张. 读九年级的哥哥想了一个办法：拿了8张扑克牌，将数字为3、4、7、9的四张给苗苗，将数字为2、5、6、8的四张留给自己，并按如下游戏方式进行确定：苗苗和哥哥从四张扑克牌中随机抽出一张，将抽出得到的两张扑克牌数字相加，如果和为偶数，则苗苗去；如果和为奇数，则哥哥去.
（1）苗苗哥哥设计的游戏规则公平吗？请画树状图或列表予以说明；
（2）如果该游戏规则不公平，请你改变一下游戏方案，使得游戏规则公平；如果该游戏规则公平，请你制订一个不公平的游戏规则.
 |
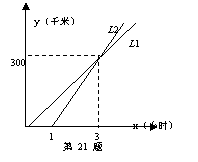
21．甲、乙两车从宜昌三峡出发，沿宜黄高速公路行驶360千米外的黄石，L 、L分别表示甲、乙两车行驶路程
（千米）与时间
（时）之间的关系（如图所示）.根据图像提供的信息，解答下列问题：
（1）求L 的函数表达式（要求写出的取值范围）；
（2）甲、乙两车哪一辆先到达黄石？该车比另一辆车早多长时间到达黄石？
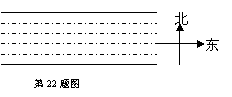
22．在一次数学活动课上，老师带领学生去测长江的宽度.某学生在长江北岸点A处观测到长江对岸水边有一点 C，测得C在A东南方向上；沿长江边向东前行200米到达B处，测得C在B南偏东30°的方向上.
（1）画出学生测量的示意图；
（2）请你根据以上数据，帮助该同学计算出长江的宽度 (精确到0.1 m).
 |
五、解答题.（本大题共3小题，每小题10分，共30分）
23．三峡大坝不仅在防洪、蓄水、发电上起着不可替代的作用，她还托起了“第四效益”——旅游.2006年宜昌共接待国内外游客930万人次，人均门票消费200元，比其他人均旅游消费的少50元；2007年宜昌市将按照“控制坝区、提升城区、辐射库区”思路，提出了实现环保旅游，增强服务功能，提高服务质量，要求人数每增长1个百分点，人均消费增长2个百分点，旅游总收入增长3.1个百分点.当2009年三峡工程整体竣工时，蓄水水位达到175米后，雄伟壮丽的三峡工程和雄奇秀美的长江三峡，将构成世界最大的国家公园，成为当今世界绝无仅有的旅游胜地.
（1）2006年全市旅游的总收入是多少亿元？
（2）按照2007年的发展思路，估计我市2009年旅游收入将达到多少亿？（结果保留三位有效数字）
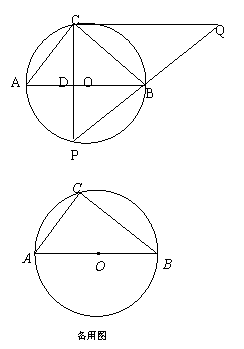
24.在⊙O中，直径AB的两侧有定点C和动点P，BC=4 、CA=3，点P在AB上运动，过点C作CP的垂线，与PB的延长线交于点Q.
（1）当点P运动到与点C关于AB对称时，求CQ的长；当点P运动到什么位置时，CQ取得最大值，并求出此时CQ的长；
（2）当点P运动到AB的中点时, 求CQ的长.
 |
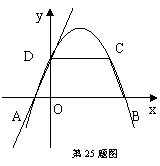
25．如图，直线y=x+2与x轴交于点A、与y轴交于点D，以AD为腰，以x轴为底作等腰梯形ABCD(AB＞CD)，且等腰梯形的面积是8，二次函数y=ax2+bx+c经过等腰梯形的四个顶点.
(1)求抛物线的解析式；
(2)若点P为x轴上的—个动点，当点P运动到什么位置时，△ADP为等腰三角形，求这时点P的坐标；
(3)若点P为抛物线上的—个动点，是否存在点P使△ADP为等腰三角形，若不存在，请说明理由；若存在，简要地进行说明有几个；并至少求出其中的一个点坐标.
 |
参 考 答 案
一、选择题.
1.A；2.D；3.B；4.D；5.B；6.D；7.B；8.D；9.B；10.C.
二、填空题.
11.80°；12.AB=CD或AD∥BC；13.6；14.126；15.6n+2.
三．解答题.
16．x=2；17．（1）略；（2）证△ACE≌△ABD，得BD=CE；18．48≤t≤75秒；19．48π；
四．解答题.
20．（1）该游戏规则不公平，列表情况如下：
| 2 | 5 | 6 | 8 | |
| 3 | 5 | 8 | 9 | 11 |
| 4 | 6 | 9 | 10 | 12 |
| 7 | 9 | 12 | 13 | 15 |
| 9 | 11 | 14 | 15 | 17 |
和为奇数的概率：，和为偶数的概率：，＞；
（2）该游戏规则不公平，只要2与3交换即可.
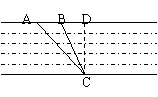21．（1）L的函数表达式y=150x-150(1≤x≤3.4)；（2）乙车先到达黄石，该车比另一辆车早0.2小时到达黄石.
22．（1）测量的示意图；
（2）设长江的宽度CD为x米，
x－x=200，x=472.8（米）.
五、解答题.
23．（1）设其它人均旅游消费为x元，x－50=200，解得x=500，
×(200+500）=元， 元=65.1亿元
（2）设人数增加y个百分点，依据题意列方程：
（1+y）×700（1+2y）=（1+3.1y），解得：y=5%
（1+5%×3.1）（1+5%×3.1）（1+5%×3.1）=元≈90.2亿元.
24．(1)当点P与点C关于AB对称时，CP⊥AB，设垂足为D.
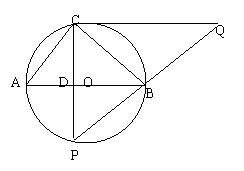∵AB为⊙O的直径，∴∠ACB=90°.
∵BC=4, AC=3，∴AB=5.
又∵AC·BC=AB·CD，∴CD=，PC=
在Rt△ACB和Rt△PCQ中，
∠ACB＝∠PCQ=90°, ∠CAB＝∠CPQ，
Rt△ACB∽Rt△PCQ，∴CQ=PC=
点P在弧AB上运动时，恒有CQ=PC, 故PC最大时，CQ取到最大值．
当PC过圆心O，即PC取最大值5时，CQ 最大值为
(2）当点P运动到弧AB的中点时，过点B作BE⊥PC于点E（如图）.
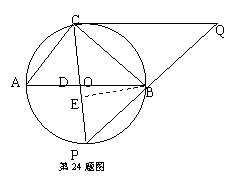∵P是弧AB的中点，
∴∠PCB=45°,CE=BE=×4=2，
又∠CPB=∠CAB
∴tan∠CPB= tan∠CAB=
∴PE=BE/tan∠CPB=BE=而从PC=PE+EC=
由（l）得， CQ=PC=
25．（1）过C作CE⊥AB于E
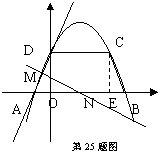则△AOD≌△BCE，四边形CDOE为矩形
∴CD=OE，AO=BE
y=x+2中x=0，y=2；x=-2，y=0
×2×（2+2+2OE）=8
∴OE=CD=2
∴C（2，2）B（4，0）
∵二次函数y=ax2+bx+c经过A、D、B三点
可以求得抛物线的解析式为：y=-x2+x+2
（2）点P为x轴上的—个动点
∵在△AOD中, ∠DOA=90°，可求得AD=4=2AO，∴∠ADO=30°，∠DAO=60°；
当P在A右边时，∵△ADP为等腰三角形，∴△ADP是等边三角形，
∴AP=AD=4 ，∴P的坐标是（2，0）；
当P在A左边时，△ADP是以A为顶点的等腰三角形，AO=AD=4，点P的坐标为（-6，0）.
（3）满足条件的抛物线上的点有四个，其中以AD为腰的等腰三角形有两个，以AD为底的等腰三角形有两个.
以AD为底的等腰三角形的点P有两个, P一定在AD的垂直平分线，由△AOD≌△AMN得：点M、N的坐标为：∴M（-1，），N（0，2），则直线MN:y=-x+，
∵二次函数: y=-x2+x+2，组成方程组解得：
x=， x=
y= y=，∴P (,),P (,).