初中数学毕业生学业考试仿真模拟试卷3

初中数学毕业生学业考试仿真模拟试卷

数　学　试　题（三）

考生注意：

1.全卷试题共五大题25小题，卷面满分120分，考试时间120分钟；

2.本试卷分为两卷，解答第Ⅰ卷（1—2页）时请将解答结果填写在第Ⅱ卷（3—8页）上指定的位置，否则答案无效；交卷时只交第Ⅱ卷；

3.做本卷试题可使用科学计算器；

以下公式共参考：

　　二次函数y=ax²+bx+c（a≠0）图象的顶点坐标是（- ，）；弧长l=πR.

第Ⅰ卷（选择题、填空题　共45分）

一、选择题.（本大题满分30分，共10小题，每小题3分）

下列各小题都给出了四个选项，其中只有一个符合题目要求，请把符合题目要求的选项前的字母代号填写在第Ⅱ卷上指定的位置.

1．计算 2 一的结果是

  A . 1　　　　 B -1　　　　 C ．　　　　 D . 5

2．分式的值为１时，的值是（　　）

Ａ．　　　　　　　Ｂ．　　　　　　　Ｃ．　　　　　　Ｄ．

3．青藏高原是世界上海拔最高的高原，它的面积约为平方千米．将用科学记数法表示应为（　　）

Ａ．　　　　　　　　Ｂ．　　　 Ｃ．　　　　　　　Ｄ．

4. 某市电视台在今年5月举办的“开心就唱”歌手大赛活动中，号召观众发短信为参赛者投支持票，投票短信每1万条为1组，每组抽出1个一等奖，3个二等奖，6个三等奖．张艺同学发了1条短信，她的获奖概率是（ 　 ）

A．　　　　　 B．　　　　　　C．　　　 　　 D．

5．下列各图中，既是轴对称图形又是中心对称图形的是　　　　　　　　　　　

A．

B．

C．

D．

6. 右表给出的是本月份的日历表，任意圈出一横或一竖列相邻的三个数，这三个数的和不可能是（　　）

日	一	二	三	四	五	六
				1	2	3
4	5	6	7	8	9	10
11	12	13	14	15	16	17
18	19	20	21	22	23	24
25	26	27	28	29	30

A．24　　　 B．43　　　 C．57　　　 D．69

7． 在甲、乙两块试验田内，对生长的禾苗高度进行

测量，分析数据得：甲、乙试验田内禾苗高度数据

的方差分别为，则这两块试

验田中

A．甲试验田禾苗平均高度较高　　　　　　　　　　

B．甲试验田禾苗长得较整齐

C．乙试验田禾苗平均高度较高　　　　　　　　　　

D．乙试验田禾苗长得较整齐

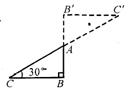8．．如图， △ ABC 中，∠B = 90 º ，∠C = 30 º　, AB = 1 ，将 △ ABC 绕顶点 A 旋转 180⁰ ，点 C落在 C ′处，则 CC′的长为

A . 4　　　　 B.4　

（第8题）

 C . 2　　　　 D . 2

9.

（第9题）

　 　　　　　　　　　　　　　　　　　　　　　　　　　　 

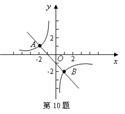10. 如图，一次函数与反比例函数的图象交于点，则使的的取值范围是

 A．　　　　　　　 B．

　C．　　  D．

二、填空题.（本大题满分15分，共5小题，每小题3分）请将下列各题的答案填写在第Ⅱ卷上指定的位置.

11.比较大小　　．

12如图，若将△ABC绕点O顺时针旋转180°后得到△A'B'C'，则A点的对应点A'点的坐标是_____________．

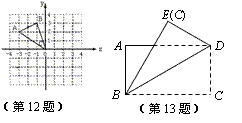
13．如图，矩形纸片ABCD，AB＝2，∠ADB＝30°，沿对角线BD折叠（使△ABD和△EBD落在同一平面内），则A、E两点间的距离为________．

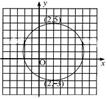
14．如图，方格纸上一圆经过（2 , 5）、（2 , -3）两点，且此两点为圆与方格纸横线的切点，则该圆圆心的坐标为　　　 。

			（第14题）		（第15题）

15. 如图，在半径为的圆内作一个内接正方形，然后作这个正方形的内切圆，又在这个内切圆中作内接正方形，依此作到第个内切圆，它的半径是　　　　

初中毕业生学业考试仿真模拟试卷

数　学　试　题（三）

题　号	一	二	三	四	五	总　分
得　分

第Ⅱ卷（ 解答题　共75分）

一、选择题答案栏.（本大题满分30分）请将第Ⅰ卷中选择题的答案填写在下表中.

得分	评卷人		题号	1	2	3	4	5	6	7	8	9	10
			答案

二、填空题答案栏.（本大题满分15分）请将第Ⅰ卷中填空题的答案填写在下表中.

得分	评卷人		题号	11	12	13	14		15
			答案

得分	评卷人

三、解答题.（本大题满分24分，共4小题，每小题6分）

16. 解方程：

17. 如图，正方形ABCD的边CD在正方形ECGF的边CE上，连结BE、DG．

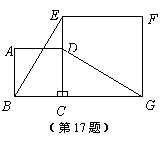（1）观察猜想BE与DG之间的大小关系，并证明你的结论．

（2）图中是否存在通过旋转能够互相重合的两个三角形？若

存在，请说出旋转过程；若不存在，请说明理由．

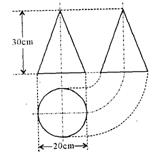18. 如图是某工件的三视图，求此工件的全面积．

　  

　

19. 在暑期社会实践活动中，小明所在小组的同学与一 家玩具生产厂家联系，给该厂组装玩具，该厂同意他们组装240套玩具.这些玩具分为A、B、C三种型号，它们的数量比例以及每人每小时组装各种型号玩具的数量如图所示：

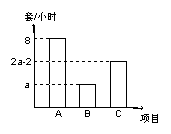若每人组装同一种型号玩具的速度都相同，根据以上信息，完成下列填空：

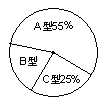
（1）从上述统计图可知，A 型玩具有　　　 套，B型玩具有　　　 套，C型玩具有　　套.

（2）若每人组装A型玩具16套与组装C型玩具12套所画的时间相同，那么的值为　　 ，每人每小时能组装C型玩具　　　　  套.

四、解答题.（本大题满分21分，共3小题，每小题7分）

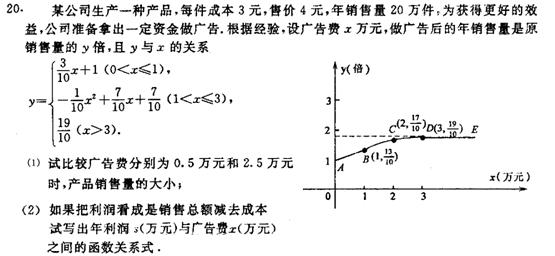
21．不透明的口袋里装有白、黄、蓝三种颜色的乒乓球（除颜色外其余都相同），其中白球有2个，黄球有1个，现从中任意摸出一个是白球的概率为.

（1）试求袋中蓝球的个数.

（2）第一次任意摸一个球（不放回），第二次再摸一个球，请用画树状图或列表格法，求两次摸到都是白球的概率.

22．一艘渔船在A处观测到东北方向有一小岛C，已知小岛C周围4.8海里范围内是水产养殖场.渔船沿北偏东30°方向航行10海里到达B处，在B处测得小岛C在北偏东60°方向，这时渔船改变航线向正东(即BD)方向航行，这艘渔船是否有进入养殖场的危险？

	（第22题）

五、解答题.（本大题满分30分，共3小题，每小题10分）

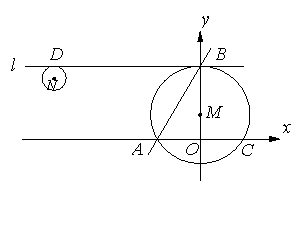
23．如图（1），在平面直角坐标系中，直线与两坐标轴分别交于A、B两点，M为y轴正半轴上一点，⊙M过A、B两点，交x轴正半轴于点C，过B作x轴的平行线，N点的坐标为（-12，5），⊙N与直线相切于点D.

（1）求∠ABO的度数及圆心M的坐标；

（2）若⊙N以每秒1个单位的速度沿直线向右平移，同时直线AB沿x轴负方向匀速平移，当⊙N第一次与⊙M相切时，直线AB也恰好与⊙N第一次相切，求直线AB每秒平移多少个单位长度？

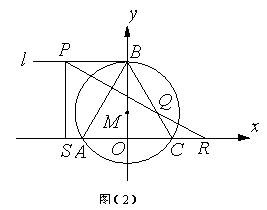
（3）如图（2），P为直线上的一个动点，过P作AB的垂线分别交线段BC、x轴于Q、R两点，过P作x轴的垂线，垂足为S（S在A点的左侧）.当P点运动时，BQ-AS的值是否改变？若不变，请求其值；若改变，请求其值变化的范围.

	图（1）
			（第2３题）

24．某学校九年级“课题学习”小组就“城镇经济发展与水资源的合理利用”课题，以进行调研：

　 基本情况：

A城镇中心区面积6平方千米，全部为平原地形，无河流过境，全部采用打井抽取地下水源供应，本次讨论按规划习惯，将水源消耗分为生活区（包括商业服务区），工业区，农业区。

基本数据：

1.　　 生活类用地0.4平方千米;

2.　　 三个基本用地类型的用水指标按当地市城镇用水标准依次为:

农业每年500立方米/亩(每日2升/);

生活每日6升/;

工业每日10升/

3．井的出水量：每口井每天出水300吨。

 4．井的数量：根据市现行的规划指标，井的分布密度最高为每200亩一口井。

问题解决：

（1）　　　 A镇中心区现有20口井，计算还需要打井的数量。（1亩≈666）

（2）　　　 A镇镇中心在实际自然条件下，最多可发展规模的工业。

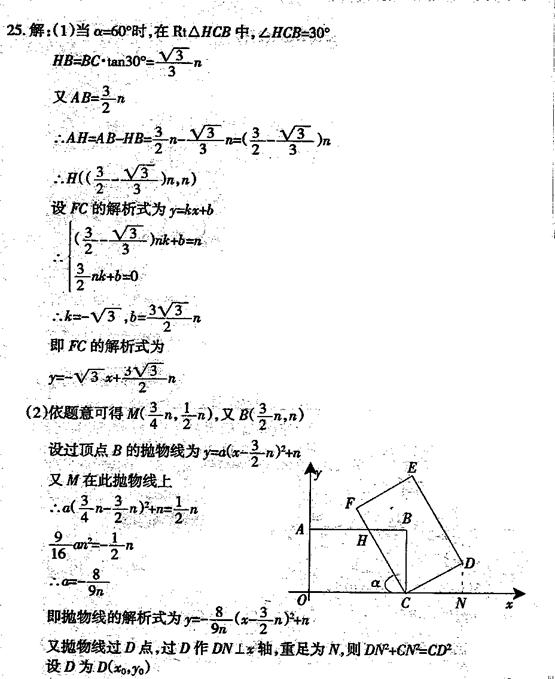
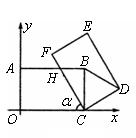
25．如图，在平面直角坐标系中，把矩形绕点顺时针旋转角，得到矩形．设与交于点，且，且（如图）．

（1）当时，求直线的解析式；

（2）若矩形的对称中心，请探究：当旋转角满足什么条件时，经过点M，且以点为顶点的抛物线经过点D．

		（第25题）

参　考　答　案

一、选择题.

1---5 BCCBC　 6----10 BADCB

二、填空题.

11．<　 12．（3，2）  13．2　 14．（2，1）　 15．

三、解答题.

16. 

17. (1)作AC的垂直平分线MN，与AC交于O点，与BE延长线交点为求作点D。　　

(2)有外接圆　

连结AD、CD，过D点作DE、DF分别垂直于AB、CB。

由△EDA≌△FDC得OA=OB=OC=OD, =25.

18.

19. (1) 132,48,60,(2) 4,6,

四、解答题.

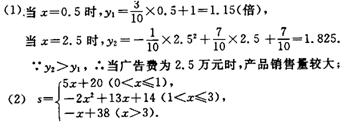20．

21. （1）设蓝球个数为x个

则由题意得＝　　解得 x＝1，即蓝球有1个　　　

　　（2）数状图或列表正确

　　　　 两次摸到都是白球的概率 ＝＝ 

22．．解法一：过点B作BM⊥AH于M，∴BM∥AF.∴∠ABM=∠BAF=30°.

　 在△BAM中，AM=AB=5，BM=.　

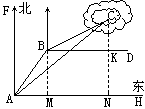　　　　过点C作CN⊥AH于N，交BD于K.

　　　　在Rt△BCK中，∠CBK=90°-60°=30°

　　　 设CK=，则BK=　　

　　　　在Rt△ACN中，∵∠CAN=90°-45°=45°，

　　　　∴AN=NC.∴AM+MN=CK+KN.

　　　　又NM=BK，BM=KN.

　　　　∴.解得

　　　 ∵5海里＞4.8海里，∴渔船没有进入养殖场的危险.　　

　　　　答：这艘渔船没有进入养殖场危险.　　

　　解法二：过点C作CE⊥BD，垂足为E，∴CE∥GB∥FA.

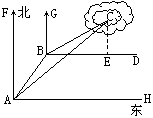　　　　∴∠BCE=∠GBC=60°.∠ACE=∠FAC=45°.

　　　　∴∠BCA=∠BCE-∠ACE=60°-45°=15°.

　　　　又∠BAC=∠FAC-∠FAB=45°-30°=15°，

∴∠BCA=∠BAC.∴BC=AB=10.

　　　　在Rt△BCE中，CE=BC·cos∠BCE=BC·cos60°=10×=5(海里).

　　　　∵5海里＞4.8海里，∴渔船没有进入养殖场的危险.

　　　答：这艘渔船没有进入养殖场的危险.

五、解答题.

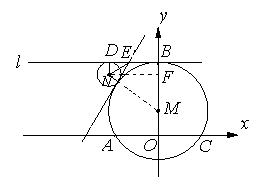23. （1）∠ABO的度数为30°，圆心M的坐标为（0，2）；

（2）如图，连结ND、NE、NM，过N作NF⊥OB于

点F，MN=5，MF=4-1=3，∴NF=4，∴⊙N平移

的距离为12-4=8（单位长度），∴平移的时间

为8秒.又∵ND=1，∠DEN=30°，∴DE=，

∴直线AB平移的距离为4-，∴直线AB

平移的速度为（单位长度/秒）

（3）∵∠PBA=∠ABC=60°，PQ⊥AB，∴BP=BQ.∵四边形PBOS为矩形，∴BP=OS，∴BQ=OS，

∴BQ-AS=OA=.