初中数学毕业生学业考试仿真模拟试卷4

初中数学毕业生学业考试仿真模拟试卷

数　学　试　题（四）

考生注意：

1.全卷试题共五大题25小题，卷面满分120分，考试时间120分钟；

2.本试卷分为两卷，解答第Ⅰ卷（1—2页）时请将解答结果填写在第Ⅱ卷（3—8页）上指定的位置，否则答案无效；交卷时只交第Ⅱ卷；

3.做本卷试题可使用科学计算器；

以下公式共参考：

　　二次函数y=ax²+bx+c（a≠0）图象的顶点坐标是（－ ，）；弧长l=πR.

第Ⅰ卷（选择题、填空题　共45分）

一、选择题.（本大题满分30分，共10小题，每小题3分）

下列各小题都给出了四个选项，其中只有一个符合题目要求，请把符合题目要求的选项前的字母代号填写在第Ⅱ卷上指定的位置.

1．已知a－=0，则a的值是

　 A.±　　  　B.－　　　　　 C.　　　　　  D.1.4

2．下列运算正确的是（　　）　

Ａ．　　　 　Ｂ．　　　　　 Ｃ．　　　　　　　Ｄ．

3. 不等式组的解集在数轴上可表示为

4．从左边看图5中的物体，得到的图形是（　　）

Ｄ．

Ｃ．

Ｂ．

Ａ．

5．一次数学测试后，随机抽取九年级二班5名学生的成绩如下：78，85，91，98，98．关于这组数据的错误说法是（　　）

Ａ．极差是20　　　　　　 Ｂ．众数是98　　　　　　 Ｃ．中位数是91　　　　　Ｄ．平均数是91

6. 一名宇航员向地球总站发回两组数据：甲、乙两颗行星的直径分别为千米和千米，这两组数据之间

Ａ．有差别　　　　Ｂ．无差别　　　 Ｃ．差别是千米 Ｄ．差别是100千米

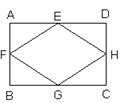
7．如图，顺次连结矩形ABCD各边中点，得到菱形EFGH。这个由矩形和菱形所组成的图形

A．是轴对称图形但不是中心对称图形　　B．是中心对称图形但不是轴对称图形

C．既是轴对称图形又是中心对称图形　　D．没有对称性

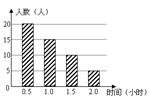
8. 某校为了了解学生课外阅读情况，随机调查了名学生各自平均每天的课外阅读时间，并绘制成条形图（如图），据此可以估计出该校所有学生平均每人每天的课外阅读时间为

Ａ．小时　　　　　　　Ｂ．小时　　　 Ｃ．小时　　　　　 Ｄ．小时

						（第8题）
		（第7题）

9. 如果⊙O₁、⊙O₂的半径分别为4、5，那么下列叙述中，错误的是

A．当O₁ O₂＝1时，⊙O₁与⊙O₂相切

B．当O₁ O₂＝5时，⊙O₁与⊙O₂有两个公共点

C．当O₁ O₂＞6时，⊙O₁与⊙O₂必有公共点

D．当O₁ O₂＞1时，⊙O₁与⊙O₂至少有两条公切线

10.　　　　　　　　　　　　　　　 

	（第10题）

二、填空题.（本大题满分15分，共5小题，每小题3分）请将下列各题的答案填写在第Ⅱ卷上指定的位置.

11. 如图是两张全等的图案，它们完全重合地叠放在一起，按住下面的图案不动，将上面图案绕点O顺时针旋转，至少旋转______度角后，两张图案构成的图形是中心对称图形.

12．如图，数轴上表示数的点是　　　　  ．

13．如图，若，与分别相交于点的平分线与相交于点，且，则　　　　　 度．

14 如图甲、乙、丙、丁为四个全等的六边形，且紧密地围绕着灰色的正方形戊，甲、乙、丙、丁、戊的每一边长都为1，则戊的面积比甲的面积的比值是　　　

15.观察下列各等式：…，写出反映这一规律的一般的等式为　　　　　　　　　　　　　　　　　　　　　  。

初中毕业生学业考试仿真模拟试卷

数　学　试　题（四）

题　号	一	二	三	四	五	总　分
得　分

第Ⅱ卷（ 解答题　共75分）

一、选择题答案栏.（本大题满分30分）请将第Ⅰ卷中选择题的答案填写在下表中.

得分	评卷人		题号	1	2	3	4	5	6	7	8	9	10
			答案

二、填空题答案栏.（本大题满分15分）请将第Ⅰ卷中填空题的答案填写在下表中.

得分	评卷人		题号	11	12	13	14		15
			答案

得分	评卷人

三、解答题.（本大题满分24分，共4小题，每小题6分）

16. 先化简，再求值：(,其中x=　(得数保留两位小数)

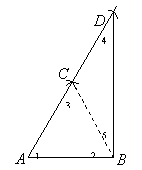
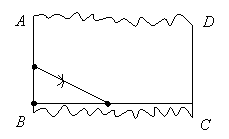
17. 某中学师生在劳动基地活动时，看到木工师傅在材料边角处画直角时，用了一种“三弧法”．方法是：

① 画线段，分别以，为圆心，长为半径画弧相交于

② 以为圆心，仍以长为半径画弧交的延长线于

③ 连结

则就是直角．

（1）请你就是直角作出合理解释．

（2）现有一长方形木块的残留部分如图，其中，整齐且平行，，是参差不齐的毛边．请你在毛边附近用尺规画一条与，都垂直的边（不写作法，保留作图痕迹）．

	（第17题）

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

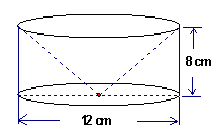
18. 如图，这是一个由圆柱体材料加工而成的零件，它是以圆柱体的上底面为底面，在其内部“掏取”一个与圆柱体等高的圆锥体而得到的，其底面直径AB =，高BC =，求这个零件的表面积；（结果保留）

	（第18题）

19. 某市平均每天产生垃圾700吨，由甲、乙两个垃圾处理厂处理。已知甲厂每小时可处理垃圾55吨，需费用550元；乙厂每小时可处理垃圾45吨，需费用495元。问：（1）甲、乙两厂同时处理该市的垃圾，每天需几小时完成？（2）如果规定该市每天用于处理垃圾的费用不得超过7370元，甲厂每天处理垃圾至少需要多少小时？

四、解答题.（本大题满分21分，共3小题，每小题7分）

20. 如图，把一个木制正方体的表面涂上颜色，然后将正方体分割成个大小相同的小正方体．从这些小正方体中任意取出一个，求取出的小正方体：

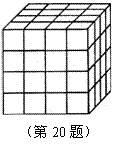（1）三面涂有颜色的概率；

（2）两面涂有颜色的概率；

（3）各个面都没有颜色的概率．

21. 施工队要修建一个横断面为抛物线的公路隧道，其高度为6米，宽度OM为12米.现以O点为原点，OM所在直线为x轴建立直角坐标系（如图所示）.

（1）直接写出点M及抛物线顶点P的坐标；

（2）求出这条抛物线的函数解析式；

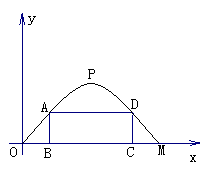（3）施工队计划在隧道门口搭建一个矩形“脚手架”CDAB，使A、D点在抛物线上，B、C点在地面OM上．为了筹备材料，需求出“脚手架”三根木杆AB、AD、DC的长度之和的最大值是多少？请你帮施工队计算一下.

	（第21题）

22．

五、解答题.（本大题满分30分，共3小题，每小题10分）

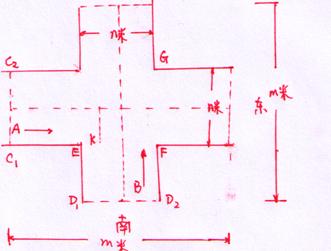
23. 张亮同学的数学“表现性作业”的选题是：

红灯绿灯等的时间差的探讨

问题提出：某十字路口，东西、南北方向的行人车辆来来往往，车水马龙，为了不让双双挤在一起，设置红绿灯，一个方向先过，另一个方向在过，在该路口的红灯绿灯的持续时间是不同的——红灯的时间比绿等的时间长，即当东西方向的红灯亮时，南北方向的绿灯要经过若干秒后才亮，这样方可确保十字路口的交通安全。

那么，如何根据实际情况设置红绿灯的时间差呢？

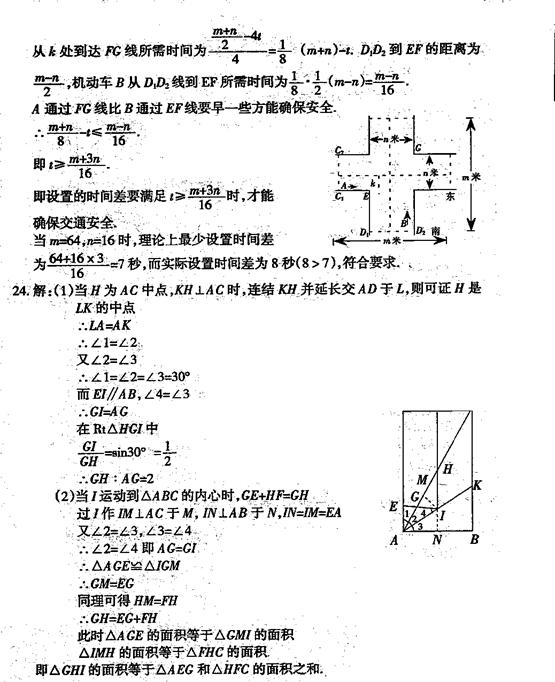
 问题假设：　如图，假设十字路口是对称的，宽窄一致，设十字路口的长为米，宽为米，当红灯亮时最后一秒出来的的骑车人A，不与另一方向绿灯亮时出来的机动车辆B相遇，即可保证安全。

数据收集：根据调查经过此路口的自行车一般的速度低于14km/h（约4m/s），机动车速度不超过28km/h（约8m/s）

　 通过上述数据和假设，你能想出张亮同学是怎样算出红绿灯的时间差，并就该长64米，宽16米的该十字路口的实际时间差的设置8s，做验证。

24．如图，已知矩形中，点I在的平分线AK上运动，过I作，垂足分别为E、F，，IE、IF分别交AC于点G、H，

（1）若点H为AC的中点，且，求∶

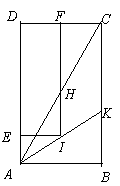（2）当点I运动到什么位置时，满足GH=GE+HF，此时矩形EIFD的面积与矩形ABCD的比值是多少？

	（第24题）

25. 已知，如图，过点A、O的圆与y轴相交于一点C，与AB相交于一点E，直线AB的解析式为y=kx+4k，过点A、O 的抛物线的顶点为P．

（1）　　　 若点C的坐标为，AC平分∠BAO，求点B的坐标；

（2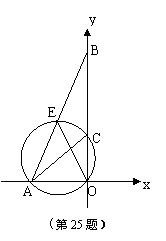）　　　 若，且点P在AB上，是否存在实数m，对于抛物线上任意一点M（x，y），都能使成立，若存在，求出m的值；若不存在，说明理由；

参　考　答　案

一、选择题.

1、A 2、C 3、D 4、B 5、D　 6、A 7、C 8、A 9、C 10、C

二、填空题.

11．180　　　12 点B　　  13　65　　　 14 　 15 　

三、解答题.

16.　原式=.∵x=,∴3(X+2)=3+6≈10.24.

17. （1）解法一：由作图知，
根据三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形，这条边所对的角就是直角，即是直角．

解法二：由作图知，所以为等边三角形．
　　 为等腰三角形，

（本题说明方法较多，只要合理均可给分）
（2）如图所示．

18. 解：这个零件的底面积 =　

　　　　这个零件的表面积 =  

　　　　圆锥母线长OB =　

　　　　这个零件的内侧面积 =　－

　　∴这个零件的表面积为：

19.（1）设甲、乙两厂同时处理，每天需x小时，得：

（55 + 45）x = 700，得，x = 7（小时）

　（2）设甲厂需要y小时，由题知：甲厂处理每吨垃圾费用为=10元，乙厂处理每吨垃圾费用为=11元。则有550y + 11（700―55y）≤7370，解得：y≥6，即甲厂每天处理垃圾至少需要6小时。

四、解答题.

20. 解：（1）因为三面涂有颜色的小正方体有8个，所以

（三面涂有颜色）

（或）；

（2）因为两面涂有颜色的小正方体有个，所以

（两面涂有颜色）（或）；

（3）因为各个面都没有涂颜色的小正方体共有8个，所以

（各个面都没有涂颜色） （或）．

21. (1)；

(2)设抛物线的函数解析式 为:，

∵抛物线过O(0,0)∴，　

∴解得∴这条抛物线的函数解析式为:

，即；

(3)设点A的坐标为，

∴OB=m，，根据抛物线的轴对称性，可得:

∴　，

即AD=12－2m，

∴=

=，

∴当m=3，即OB=3米时，三根木杆长度之和的最大值为15米.

22．

五、解答题.