初中数学竞赛模拟试题(1)
一、选择题(每小题6分,共30分)
1.方程![]() 的所有整数解的个数是(
)个
的所有整数解的个数是(
)个
(A)2 (B)3 (C)4 (D)5
2.设△ABC的面积为1,D是边AB上一点,且![]() .若在边AC上取一点E,
.若在边AC上取一点E,
使四边形DECB的面积为![]() ,则
,则![]() 的值为(
)
的值为(
)
 (A)
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
3.如图所示,半圆O的直径在梯形ABCD的底边AB上,且与其余三边BC,CD,DA相切,若BC=2,DA=3,则AB的长( )
(A)等于4 (B)等于5 (C)等于6 (D)不能确定
4.在直角坐标系中,纵、横坐标都是整数的点,称为整点。设![]() 为整数,当直线
为整数,当直线![]() 与直线
与直线![]() 的交点为整点时,
的交点为整点时,![]() 的值可以取(
)个
的值可以取(
)个
(A)8个 (B)9个 (C)7个 (D)6个
5.世界杯足球赛小组赛,每个小组4个队进行单循环比赛,每场比赛胜队得3分,败队得0分,平局时两队各得1分.小组赛完后,总积分最高的2个队出线进入下轮比赛.如果总积分相同,还有按净胜球数排序.一个队要保证出线,这个队至少要积( )分.
(A)5 (B)6 (C)7 (D)8
二、填空题(每小题6分,共30分)
6.当![]() 分别等于
分别等于![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 时,计算代数式
时,计算代数式![]() 的值,将所得的结果相加,其和等于
.
的值,将所得的结果相加,其和等于
.
 7.关于
7.关于![]() 的不等式
的不等式![]() >
>![]() 的解是
的解是![]() <
<![]() ,则关于
,则关于![]() 的不等式
的不等式![]() <0的解为
.
<0的解为
.
8.方程![]() 的两根都是非零整数,且
的两根都是非零整数,且![]() ,则
,则![]() = .
= .
9.如图所示,四边形ADEF为正方形,ABCD为等腰直角三角形,D在BC边上,△ABC的面积等于98,BD∶DC=2∶5.则正方形ADEF的面积等于 .
10.设有![]() 个数
个数![]() ,
,![]() ,…,
,…,![]() ,它们每个数的值只能取0,1,-2三个数中的一个,且
,它们每个数的值只能取0,1,-2三个数中的一个,且![]() …
…![]() ,
,![]() …
…![]() ,则
,则![]() …
…![]() 的值是
.
的值是
.
三、解答题(每小题15分,共60分)
11.如图,凸五边形ABCDE中,已知S△ABC=1,且EC∥AB,AD∥BC,BE∥CD,
 CA∥DE,DB∥EA.试求五边形ABCDE的面积.
CA∥DE,DB∥EA.试求五边形ABCDE的面积.
12.在正实数范围内,只存在一个数是关于![]() 的方程
的方程![]() 的解,求实数
的解,求实数![]() 的取值范围.
的取值范围.
 13.如图,一次函数的图象过点P(2,3),交x轴的正半轴与A,交y轴的正半轴与B,求△AOB面积的最小值.
13.如图,一次函数的图象过点P(2,3),交x轴的正半轴与A,交y轴的正半轴与B,求△AOB面积的最小值.
14.预计用1500元购买甲商品![]() 个,乙商品
个,乙商品![]() 个,不料甲商品每个涨价1.5元,乙商品每个涨价1元,尽管购买甲商品的个数比预定数减少10个,总金额仍多用29元.又若甲商品每个只涨价1元,并且购买甲商品的数量只比预定数少5个,那么甲、乙两商品支付的总金额是1563.5元.
个,不料甲商品每个涨价1.5元,乙商品每个涨价1元,尽管购买甲商品的个数比预定数减少10个,总金额仍多用29元.又若甲商品每个只涨价1元,并且购买甲商品的数量只比预定数少5个,那么甲、乙两商品支付的总金额是1563.5元.
(1)求![]() 、
、![]() 的关系式;
的关系式;
(2)若预计购买甲商品的个数的2倍与预计购买乙商品的个数的和大于205,但小于210,求![]() 、
、![]() 的值.
的值.
参考答案
一、选择题
1.C 2.B 3.B 4.A 5.C
二、填空题
6.6 7.![]() 8.-202 9.116 10.-125
8.-202 9.116 10.-125
三、解答题
11.∵ BE∥CD,CA∥DE,DB∥EA,EC∥AB,AD∥BC,
∴ S△BCD=S△CDE=S△DEA=S△EAB=S△ACB=S△ACF=1.
设S△AEF=![]() ,则S△DEF=
,则S△DEF=![]() ,
,
又△AEF的边AF与△DEF的边DF上的高相等,
所以,![]() ,而△DEF∽△ACF,则有
,而△DEF∽△ACF,则有
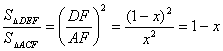 .
.
整理解得 ![]() .
.
故SABCDE=3S△ABC+S△AEF=![]() .
.
12.原方程可化为![]() ,①
,①
(1)当△=0时,![]() ,
,![]() 满足条件;
满足条件;
(2)若![]() 是方程①的根,得
是方程①的根,得![]() ,
,![]() .此时方程①的另一个根为
.此时方程①的另一个根为![]() ,故原方程也只有一根
,故原方程也只有一根![]() ;
;
(3)当方程①有异号实根时,![]() ,得
,得![]() ,此时原方程也只有一个正实数根;
,此时原方程也只有一个正实数根;
(4)当方程①有一个根为0时,![]() ,另一个根为
,另一个根为![]() ,此时原方程也只有一个正实根。
,此时原方程也只有一个正实根。
综上所述,满足条件的![]() 的取值范围是
的取值范围是![]() 或
或![]() 或
或![]() .
.
13.解:设一次函数解析式为![]() ,则
,则![]() ,得
,得![]() ,令
,令![]() 得
得![]() ,则OA=
,则OA=![]() .
.
令![]() 得
得![]() ,则OA=
,则OA=![]() .
.
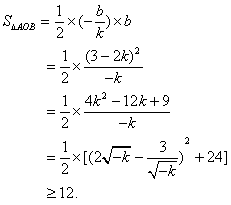
所以,三角形AOB面积的最小值为12.
14.(1)设预计购买甲、乙商品的单价分别为![]() 元和
元和![]() 元,则原计划是
元,则原计划是
![]() , ①
, ①
由甲商品单价上涨1. 5元、乙商品单价上涨1元,并且甲商品减少10个的情形,得
![]() .②
.②
再由甲商品单价上涨1元,而数量比预计数少5个,乙商品单价上涨仍是1元的情形,得
![]() , ③
, ③
由①、②、③得
|
④-⑤×2并化简,得
![]() .
.
(2)依题意,有205<![]() <210及
<210及![]() ,54<
,54<![]() <
<![]() ,
,
由![]() 是整数,得
是整数,得![]() ,从而得
,从而得![]() .
.
答:(1)![]() 、
、![]() 的关系
的关系![]() ;
;
(2)预计购买甲商品76个,乙商品55个.
初中数学竞赛模拟试题(2)
一、选择题(每小题6分,共30分)
1.已知![]() ,
,![]() ,则
,则![]() =(
)
=(
)
(A)4 (B)0 (C)2 (D)-2
2.方程![]() 的实根的个数为(
)
的实根的个数为(
)
(A)1 (B)2 (C)3 (D)4
3.已知梯形ABCD中,AD∥BC,对角线AC、BD交于O,△AOD的面积为4,
△BOC的面积为9,则梯形ABCD的面积为( )
(A)21 (B)22 (C)25 (D)26
4.已知⊙O1与⊙O2是平面上相切的半径均为1的两个圆,则在这个平面上有( )个半径为3的圆与它们都相切.
(A)2 (B)4 (C)5 (D)6
5.一个商人用![]() 元(
元(![]() 是正整数)买来了
是正整数)买来了![]() 台(
台(![]() 为质数)电视机,其中有两台以成本的一半价钱卖给某个慈善机构,其余的电视机在商店出售,每台盈利500元,结果该商人获得利润为5500元,则
为质数)电视机,其中有两台以成本的一半价钱卖给某个慈善机构,其余的电视机在商店出售,每台盈利500元,结果该商人获得利润为5500元,则![]() 的最小值是(
)
的最小值是(
)
(A)11 (B)13 (C)17 (D)19
二、填空题(每小题6分,共30分)
6.已知等腰△ABC内接于半径为5cm的⊙O,若底边BC=8cm,则△ABC的面积为 .
7.△ABC的三边长![]() 、
、![]() 、
、![]() 满足
满足![]() ,
,![]() ,则△ABC的周长等于
.
,则△ABC的周长等于
.
8.若![]() 表示不超过
表示不超过![]() 的最大整数,且满足方程
的最大整数,且满足方程![]() ,则
,则![]() =
.
=
.
9.若直线![]() 与直线
与直线![]() 的交点坐标是(
的交点坐标是(![]() ,
,![]() ),则
),则![]() 的值是
.
的值是
.
10.抛物线![]() 向左平移3个单位,再向上平移两个单位,得抛物线C,则C关于
向左平移3个单位,再向上平移两个单位,得抛物线C,则C关于![]() 轴对称的抛物线解析式是
.
轴对称的抛物线解析式是
.
三、解答题(每小题15分,共60分)
 11.如图所示,在△ABC中,AC=7,BC=4,D为AB的中点,E为AC边上一点,且∠AED=90°+
11.如图所示,在△ABC中,AC=7,BC=4,D为AB的中点,E为AC边上一点,且∠AED=90°+![]() ∠C,求CE的长.
∠C,求CE的长.
12.某公交公司停车场内有15辆车,从上午6时开始发车(6时整第一辆车开出),以后每隔6分钟再开出一辆.第一辆车开出3分钟后有一辆车进场,以后每隔8分钟有一辆车进场,进场的车在原有的15辆车后依次再出车.问到几点时,停车场内第一次出现无车辆?
13.已知一个两位数,其十位与个位数字分别为![]() 、
、![]() ,二次函数
,二次函数![]() 的图象与
的图象与![]() 轴交于不同的两点A、B,顶点为C,且S△ABC≤1.
轴交于不同的两点A、B,顶点为C,且S△ABC≤1.
(1)求![]() 的取值范围;(2)求出所有这样的两位数
的取值范围;(2)求出所有这样的两位数![]() .
.
14.已知![]() 是正整数,且
是正整数,且![]() 与
与![]() 都是完全平方数.是否存在
都是完全平方数.是否存在![]() ,使得
,使得![]() 是质数?如果存在,请求出所有
是质数?如果存在,请求出所有![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
参考答案
一、选择题
1.B 2.A 3.C 4.D 5.C
二、填空题
6.8cm2或32cm2 7.14 8.![]() 9.2010 10.
9.2010 10.![]()
三、解答题
11.作BF∥DE交AC于F,作∠ACB的平分线交AB于G,交BF于H.
则∠AED=∠AFB=∠CHF+![]() ∠C。
∠C。
因为∠AED=90°+![]() ∠C,所以∠CHF=90°=∠CHB。
∠C,所以∠CHF=90°=∠CHB。
 又∠FCH=∠BCH,CH=CH。
又∠FCH=∠BCH,CH=CH。
∴ △FCH≌△BCH。
∴ CF=CB=4,
∴ AF=AC-CF=7-4=3。
∵ AD=DB,BF∥DE,
∴ AE=EF=1.5,
∴ CE=5.5.
12.设从6时起x分钟时停车场内第一次出现无车辆,此时总共出车S辆,进场车y辆,则
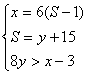
∴ ![]() , 解得
, 解得 ![]() .
.
∵ S为正整数,∴ S=56,即到第56辆车开出后,停车场内第一次出现无车
辆.此时![]() ,6+
,6+![]() =11.5(时)
=11.5(时)
答:到11时30分时,停车场内第一次出现无车辆.
13.(1)设A(![]() ,0),B(
,0),B(![]() ,0),(
,0),(![]() ),则
),则![]() 、
、![]() 是方程
是方程
![]() 的两个不同的实根,所以
的两个不同的实根,所以
![]() ,
,![]() ,
,![]() .
.
又![]() (
(![]() 表示点C的纵坐标),所以
表示点C的纵坐标),所以
S△ABC=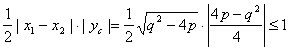 ,
,
从而![]() ,
,![]() .
.
故0<![]() .
.
(2)由(1)知,![]() 1,2,3,4.
1,2,3,4.
因为![]() 被4除余数为0或1,故
被4除余数为0或1,故![]() 被4除余数也是0或1,从而
被4除余数也是0或1,从而![]() 1,或4.这两个方程中符合题意的整数解有
1,或4.这两个方程中符合题意的整数解有![]()
![]()
![]()
![]()
故所有两位数![]() 为23,65,34,86.
为23,65,34,86.
14.设![]() ,
,![]() ,其中
,其中![]() ,
,![]() 都是正整数,则
都是正整数,则
![]() .
.
若![]() ,则
,则![]() 不是质数.
不是质数.
若![]() ,则
,则![]() ,于是
,于是
![]()
![]() ,矛盾.
,矛盾.
综上所述,不存在正整数![]() ,使得
,使得![]() 是质数.
是质数.
初中数学竞赛模拟试题(3)
一、选择题(每小题6分,共30分)
1.在一个凸![]() 边形的纸板上切下一个三角形后,剩下的是一个内角和为2160°的多边形,则
边形的纸板上切下一个三角形后,剩下的是一个内角和为2160°的多边形,则![]() 的值为(
)
的值为(
)
(A)只能为12 (B)只能为13 (C)只能为14 (D)以上都不对
2.已知关于![]() 的方程
的方程![]() 有两个不同的实数根,则实数
有两个不同的实数根,则实数![]() 的取值范围是(
)
的取值范围是(
)
(A)![]() =0 (B)
=0 (B)![]() ≥0 (C)
≥0 (C)![]() =-2 (D)
=-2 (D)![]() >0或
>0或![]() =-2
=-2
3.若正实数![]() 、
、![]() 满足
满足![]() ,则
,则![]() 的最小值为(
)
的最小值为(
)
(A)-7 (B)0 (C)9 (D)18
4.如图,在△ABC中,∠C=Rt∠,CD⊥AB,下列结论:(1)DC·AB=AC·BC;
(2)![]() ; (3)
; (3)![]() ;(4)AC+BC>CD+AB.
;(4)AC+BC>CD+AB.
其中正确的个数是( )
(A)4 (B)3 (C)2 (D)1
5.设![]() 是正整数,0<
是正整数,0<![]() ≤1,在△ABC中,如果AB=
≤1,在△ABC中,如果AB=![]() ,BC=
,BC=![]() ,CA=
,CA=![]() ,BC边上的高AD=
,BC边上的高AD=![]() ,那么,这样的三角形共有(
)
,那么,这样的三角形共有(
)
(A)10个 (B)11个 (C)12个 (D)无穷多个
二、填空题(每小题6分,共30分)
6.实数![]() 、
、![]() 、
、![]() 满足:
满足:![]() ,
,![]() ,则
,则![]() 的值为
.
的值为
.
7.如果对于任意两个实数![]() 、
、![]() ,“
,“![]() ”为一种运算,定义为
”为一种运算,定义为![]() ,则函数
,则函数![]() (-3≤
(-3≤![]() ≤3)的最大值与最小值的和为
.
≤3)的最大值与最小值的和为
.
8.已知四个正数![]() 、
、![]() 、
、![]() 、
、![]() 满足
满足![]() <
<![]() <
<![]() <
<![]() ,它们两两的和依从小到大的次序分别是:23、26、29、93、
,它们两两的和依从小到大的次序分别是:23、26、29、93、![]() 、
、![]() ,则
,则![]() 的值为
.
的值为
.
9.已知点P在直角坐标系中的坐标为(0,1),O为坐标原点,∠QPO=150°,且P到Q的距离为2,则Q的坐标为 .
10.在△ABC中,AB=15,AC=13,高AD=12,设能完全覆盖△ABC的圆的半径为R.则R的最小值是 .
三、解答题(每小题15分,共60分)
11.实数![]() 与
与![]() 使得
使得![]() ,
,![]() ,
,![]() ,
,![]() 四个数中的三个有相同的数值,求出所有具有这样性质的数对(
四个数中的三个有相同的数值,求出所有具有这样性质的数对(![]() ,
,![]() ).
).
 12.如图,△ABC的面积为S,作直线
12.如图,△ABC的面积为S,作直线![]() ∥BC,分别交AB、AC与点D、E,若△BED的面积为K.求证:K≤
∥BC,分别交AB、AC与点D、E,若△BED的面积为K.求证:K≤![]() S.
S.
13.如图,在直角坐标系内有两个点A(-1,-1),B(2,3),若M为x轴上一点,且使MB-MA最大,求M点的坐标,并说明理由.
 |
14.在△ABC中,AB=40,AC=60,以A为圆心,AB长为半径作圆交BC与D,且D在BC边上,若BD和DC的长均为正整数,求BC的长.
参考答案
一、选择题
1.D 2.D 3.D 4.B 5.C
一、填空题
6.0 7.37 8.195 9.(1,![]() ),(-1,
),(-1,![]() ) 10.
) 10.![]() 或
或![]()
二、解答题
11.显然,![]() ,所以
,所以![]() .
.
依题意,有![]() 或
或![]() ,于是
,于是
(1)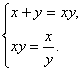 解得
解得![]() 或
或![]() .
.
当![]() 时,
时,![]() (舍去);
(舍去);
当![]() 时,
时,![]() ,无解;
,无解;
当![]() 时,
时,![]() ,∴
,∴![]() ,∴
,∴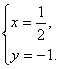
(2)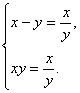 解得
解得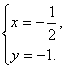
故数对(![]() ,
,![]() )为(
)为(![]() ,-1),(
,-1),(![]() ,-1).
,-1).
12.设![]() ,
,
∵
![]() ∥BC,∴
∥BC,∴ ![]() ,
,
由![]() ,得
,得
∴![]() .
.
又![]() .
.
∴
![]() .
.
13.作点A关于![]() 轴的对称点A',作直线BA'交
轴的对称点A',作直线BA'交![]() 轴于点M,由对称性知MA'=MA,MB-MA=MB-MA'=A'B.
轴于点M,由对称性知MA'=MA,MB-MA=MB-MA'=A'B.
若N是![]() 轴上异于M的点,则NA'=NA,这时NB-NA=NB-NA'<
轴上异于M的点,则NA'=NA,这时NB-NA=NB-NA'<
A'B=MB-MA.
所以,点M就是使MB-MA的最大的点,MB-MA的最大值为A'B.
设直线A'B的解析式为![]() ,则
,则
![]() 解得
解得![]() ,
,![]() .
.
即直线A'B的解析式为![]() ,令
,令![]() ,得
,得![]() .
.
故M点的坐标为(![]() ,0).
,0).
 |
14.设BD=![]() ,CD=
,CD=![]() ,(
,(![]() ,
,![]() 为正整数)
为正整数)
作AE⊥BD,垂足为E,则AB=AD=40,BE=DE=![]() .
.
∵
![]() ,
,![]() ,
,
∴
![]() ,
,
∴
![]() ,
,
∵ 20<![]() <100,
<100,
∴
只有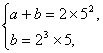 或
或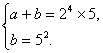
故BC的长为50或80.
初中数学竞赛模拟试题(4)
一、选择题(每小题6分,共30分)
1.若![]() 、
、![]() 都是质数,且
都是质数,且![]() ,则
,则![]() 的值等于(
)
的值等于(
)
(A)2004 (B)2007 (C)2005 (D)2008
2.一个凸多边形恰好有三个内角是钝角,这样的多边形的边数的最大值是( )
(A)5 (B)6 (C)7 (D)8
3.已知![]() ,且-2≤
,且-2≤![]() ≤1,则
≤1,则![]() 的最大值与最小值的和是(
)
的最大值与最小值的和是(
)
(A)-1 (B)2 (C)4 (D)5
4.在△ABC中,若∠A=58°,AB>BC,则∠B的取值范围是( )
(A)0°<∠B<64° (B)58°<∠B<64°
(C)58°<∠B<122° (D)64°<∠B<122°
5.直线![]() 与
与![]() 轴的交点分别为A、B,如果S△AOB≤1,那么,
轴的交点分别为A、B,如果S△AOB≤1,那么,![]() 的取值范围是( )
的取值范围是( )
(A)![]() ≤1 (B)0<
≤1 (B)0<![]() ≤1 (C)-1≤
≤1 (C)-1≤![]() ≤1 (D)
≤1 (D)![]() ≤-1或
≤-1或![]() ≥1
≥1
二、填空题(每小题6分,共30分)
6.若实数![]() 满足
满足![]() <
<![]() <
<![]() ,则不等式
,则不等式![]() >
>![]() 的解集为 .
的解集为 .
7.设![]() 、
、![]() 是方程
是方程![]() 的两个实根,且
的两个实根,且![]() .则
.则![]() 的值是 .
的值是 .
8.在直角坐标系中,![]() 轴上的动点M(
轴上的动点M(![]() ,0)到定点P(5,5)、Q(2,1)的距离分别为MP和MQ,那么当MP+MQ取最小值时,点M的横坐标
,0)到定点P(5,5)、Q(2,1)的距离分别为MP和MQ,那么当MP+MQ取最小值时,点M的横坐标![]() =
.
=
.
9.从等边三角形内一点向三边作垂线,已知这三条垂线的长分别为1,3,5.则这个等边三角形的面积是 .
10.若正整数![]() 、
、![]() 、
、![]() 满足
满足![]() ,
,![]() ,则
,则![]() 的最大值是
.
的最大值是
.
三、解答题(每小题15分,共60分)
| A | B | C | |
| 甲 | 10 | 5 | 6 |
| 乙 | 4 | 8 | 15 |
11.甲、乙两个蔬菜基地,分别向A、B、C三个农贸市场提供同品种蔬菜,按签订的合同规定向A提供45t,向B提供75t,向提供40t.甲基地可安排60t,乙基地可安排100t.甲、乙与A、B、C的距离千米数如表1,设运费为1元/(km·t).问如何安排使总运费最低?求出最小的总运费值.
12.已知![]() 为质数,使二次方程
为质数,使二次方程![]() 的两根都是整数.求出
的两根都是整数.求出![]() 的所有可能值.
的所有可能值.
13.已知CA=CB=CD,过A,C,D三点的圆交AB于点F.求证:CF为∠DCB的平分线.
 |
14.一支科学考察队前往某条河流的上游去考察一个生态区.他们出发后以每天17km的速度前进,沿河岸向上游行进若干天后到达目的地,然后在生态区考察了若干天,完成任务后以每天25km的速度返回.在出发后的第60天,考察队行进了24km后回到出发点.试问:科学考察队在生态区考察了多少天?
参考答案
一、选择题
1.C 2.B 3.B 4.A 5.C
二、填空题
6.![]() 7.1 8.
7.1 8.![]() 9.
9.![]() 10.1008.
10.1008.
三、解答题
11.设乙基地向A提供![]() ,向B提供
,向B提供![]() ,向C提供
,向C提供![]()
![]() ,则甲基地向A提供
,则甲基地向A提供![]() ,向B提供
,向B提供![]() ,向C提供
,向C提供![]() .
.
依题意,总运费为
![]()
![]() .
.
∵0≤![]() ≤100,0≤
≤100,0≤![]() ≤45,当且仅当
≤45,当且仅当![]() ,
,![]() 时,
时,![]() 有最小值,则
有最小值,则
![]() (元).
(元).
答:安排甲基地向A提供0![]() ,向B提供20
,向B提供20![]() ,向C提供40
,向C提供40![]() ;安排乙基地向A提供45
;安排乙基地向A提供45![]() ,向B提供55
,向B提供55![]() ,向C提供0
,向C提供0![]() ,可使总运费最低,最小的总运费为960元.
,可使总运费最低,最小的总运费为960元.
12.因为已知的整系数二次方程有整数根,所以
△=![]() 为完全平方数,
为完全平方数,
从而,![]() 为完全平方数.
为完全平方数.
设![]() ,注意到
,注意到![]() ,故
,故![]() ,且
,且![]() 为整数.
为整数.
于是,![]() ,则
,则![]() ,
,![]() 中至少有一个是5的倍数,即
中至少有一个是5的倍数,即
![]() (
(![]() 为正整数).
为正整数).
因此,![]() ,
,![]() .
.
由![]() 是质数,
是质数,![]() >1,知
>1,知![]() ,
,![]() 3或7.
3或7.
当![]() 时,已知方程变为
时,已知方程变为![]() ,解得
,解得![]() ,
,![]() ;
;
当![]() 时,已知方程变为
时,已知方程变为![]() ,解得
,解得![]() ,
,![]() .
.
所以![]() 3或
3或![]() 7.
7.
13.连结DF,BD,
∵ AC=CB=CD,
∴∠A=∠2,∠CDB=∠CBD,
∵∠A=∠1,∴∠1=∠2,∴∠FDB=∠FBD,∴DF=BF.
又∠1=∠2,CD=CB,∴△DCF≌△BCF,∴∠DCF=∠BCF.
即CF为∠DCB的平分线.
 |
14.设考察队到生态区用了![]() 天,考察了
天,考察了![]() 天,则
天,则
![]() ,即
,即![]() .
.
∴ ![]() (
(![]() 为整数)
为整数)
由![]() 解得
解得![]() ,所以
,所以![]() .
.
于是,![]()
答:科学考察队在生态区考察了23天.