第十四章 轴对称单元测试
检测时间：90分钟 满分：120分
一、选择题（每小题3分，共21分）
1．线段是轴对称图形，它的对称轴的条数是（ ）
A．1条 B．2条 C．3条 D．4条
2．点（4，5）关于x=1的对称点的坐标是（ ）
A．（-4，5） B．（4，-5） C．（-2，5） D．（5，5）
3．等腰三角形的两边长分别为10cm，6cm，则它的周长为（ ）
A．26cm B．22cm C．26cm或22cm D．以上都不正确
4．△ABC中，∠C=90°，∠A=30°，AB的中垂线交AC于D，交AB于E，则AC和CD的关系是（ ）
A．AC=2DC B．AC=3DC C．AC=
DC D．无法确定
5．具有下列条件的两个等腰三角形，不能判断它们全等的是（ ）
A．顶角和底边对应相等; B．两腰对应相等
C．底角和底边对应相等; D．底边对应相等，且周长相等
6．等腰三角形的底角为45°，腰长为a，则此三角形的面积为（ ）
A．a2 B．
a2 C．
a2 D．以上答案都不对
7．正五角星的对称轴有（ ）
A．1条 B．2条 C．5条 D．10条
二、填空题（每小题3分，共21分）
1．设A，B关于直线EF对称，则AB______EF．
2．关于直线EF对称的两个图形_________（填“一定”或“不一定”）全等．
3．在等腰△ABC中，∠A=108°，D，E是BC上的两点，且BD=AD，AE=EC，则图中共有_______个等腰三角形．
4．在△ABC中，高AD，BE交于O点，且BO=AC，则∠ABC=________．
5．等腰三角形有一底角的外角为105°，那么它的顶角的度数为________．
6．在△ABC中，AB=AC，∠BAC=120°，AB的垂直平分线交BC于D，且BD=10cm，则DC=_________．
7．在△ABC中，∠A=78°，点D，E，F分别在边BC，AB，AC上，BD=BE，CD=CF，则∠EDF=_______．
三、竞技平台（每小题8分，共16分）
1．如图所示，AD是△ABC的角平分线，且AC=AB+BD，∠C=30°，求∠BAC的度数．
2．如图所示，在△ABC中，AB=AC，点O在△ABC内，且∠OBC=∠OCA，∠BOC=110°，求∠A的度数．
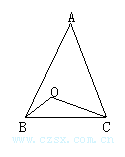
四、能力提高（每小题8分，共32分）
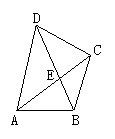
1．如图所示，在四边形ABCD中，对角线AC与BD相交于点E，若AC平分∠DAB，且AB=AE，AC=AD，求证∠DBC=∠DAB．
2．如图所示，△ABC中，已知∠B和∠C的平分线相交于点F，过点F作DE∥BC，交AB于点D，交AC于点E，若BD+CE=9，求线段DE的长．
3．如图所示，∠AOP=∠BOP=15°，PC∥OA，PD⊥OA，若PC=4，求PD的长．
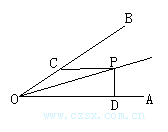
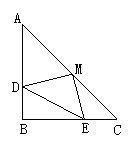
4．如图所示，在△ABC中，∠B=90°，AB=BC，BD=CE，M是AC边的中点，求证△DEM是等 腰三角形．
五、拓展创新（每小题15分，共30分）
1．如图所示，△ABC中，D，E在BC上，且DE=EC，过D作DF∥BA，交AE于点F，DF=AC，求证AE平分∠BAC．
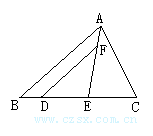
2．如图所示，等边三角形ABC中，AB=2，点P是AB边上的任意一点（点P可以与点A重合，但不与点B重合），过点P作PE⊥BC，垂足为E，过E作EF⊥AC，垂足为F，过F作FQ⊥AQ，垂足为Q，设BP=x，AQ=y．
（1）写出y与x之间的函数关系式；
（2）当BP的长等于多少时，点P与点Q重合？
答案:
一、1．B 2．C 3．C 4．B 5．B 6．B 7．C
二、1．垂直平分 2．一定 3．6 4．45° 5．30° 6．20cm 7．51°
三、1．解：在AC边上取一点E，使AE=AB，连接DE，
在△BAD和△EAD中，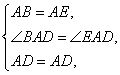
所以△BAD≌△EAD（SAS），所以BD=DE，
因为AC=AB+BD，所以AC=AE+DE，
又因为AC=AE+EC，所以DE=EC，
所以∠EDC=∠C=30°，
所以∠AED=∠EDC+∠C=60°，
因为△BAD≌△EAD，所以∠B=∠AED=60°，
所以∠BAC=180°-∠B-∠C=90°．
2．解：因为AB=AC，所以∠ABC=∠ACB，
又因为∠OBC=∠OCA，
所以∠ABC+∠ACB=2（∠OBC+∠OCB），
因为∠BOC=110°，所以∠OBC+∠OCB=70°，
所以∠ABC+∠ACB=140°，
所以∠A=180°-（∠ABC+∠ACB）=40°．
四、1．证明：在△DAE和△CAB中，
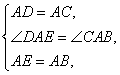
所以△DAE≌△CAB（SAS），
所以∠BDA=∠ACB，
又因为∠AED=∠CEB，
所以∠ADE+∠AED=∠ACB+∠CEB，
因为∠DAE=180°-（∠ADE+∠AED），∠DBC=180°-（∠ACB+∠CEB），
所以∠DAE=∠DBC，
因为∠DAE=∠DAB，所以∠DBC=∠DAB．
2．解：因为DE∥BC，
所以∠DFB=∠FBC，∠EFC=∠FCB，
因为∠FBC=∠FBD，∠FCB=∠FCE，
所以∠FBD=∠DFB，∠FCE=∠EFC，
所以BD=DF，CE=EF，
所以BD+CE=DF+FE=DE，
所以DE=BD+CE=9．
3．解：过P作PE⊥OB于E，
因为∠AOP=∠BOP=15°，PD⊥OA，
所以PD=PE，
因为PC∥OA，所以∠BCP=∠BOA=30°，
在Rt△PCE中，PE=PC，所以PE=×4=2，
因为PE=PD，所以PD=2．
4．证明：连接BM，
因为AB=BC，AM=MC，所以BM⊥AC，且∠ABM=∠CBM=∠ABC=45°，
因为AB=AC，所以∠A=∠C=
=45°，
所以∠A=∠ABM，所以AM=BM，
因为BD=CE，AB=BC，
所以AB-BD=BC-CE，即AD=BE，
在△ADM和△BEM中，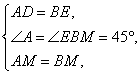
所以△ADM≌△BEM（SAS），
所以DM=EM，所以△DEM是等腰三角形．
五、1．证明：延长FE到G，使EG=EF，连接CG，
在△DEF和△CEG中，
ED=EC，∠DEF=∠CEG，FE=EG，
所以△DEF≌△CEG，所以DF=GC，∠DFE=∠G，
因为DF∥AB，所以∠DFE=∠BAE，
因为DF=AC，所以GC=AC，
所以∠G=∠CAE，
所以∠BAE=∠CAE，即AE平分∠BAC．
2．解：（1）因为△ABC为等边三角形，
所以∠A=∠B=∠C=60°，AB=BC=CA=2．
在△BEP中，因为PE⊥BE，∠B=60°，
所以∠BPE=30°，
而BP=x，所以BE=x，EC=2-x，
在△CFE中，因为∠C=60°，EF⊥CF，
所以∠FEC=30°，所以FC=1-x，
同理在△FAQ中，可得AQ=+
x，
而AQ=y，所以y=+x（0<x≤2）．
（2）当点P与点Q重合时，有AQ+BP=AB=2，
所以x+y=2，所以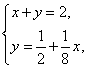
解得x=
．
所以当BP的长为时，点P与点Q重合．