初中毕业学业考试数学试卷
|
题号 | 一 | 二 | 三 | 四 | 五 |
合计 | |||||
| 16 | 17 | 18 | 19 | 20 | 21 | 22 | |||||
| 得分 | |||||||||||
说明:1.全卷共8页,考试时间为90分钟,满分120分。
2.答卷前,考生必须将自己的姓名、准考证号、学校按要求填写在密封线左边的空格内。
3.答题可用黑色或蓝色钢笔、圆珠笔按各题要求答在试卷上,但不能用铅笔或红笔。
4.考试结束时,将试卷交回。
 一、选择题(本大题共5小题,每小题3分,共15分)在每小题给出的四个选项中,只有一个是正确的,请将所选选项的字母写在题目后面的括号内。
一、选择题(本大题共5小题,每小题3分,共15分)在每小题给出的四个选项中,只有一个是正确的,请将所选选项的字母写在题目后面的括号内。
1.下列计算正确的是( )
A.-1+1=0 B.- 2-2=0 C.3÷![]() =1 D.52=10
=1 D.52=10
2.函数![]() 中自变量x的取值范围是 ( )
中自变量x的取值范围是 ( )
A.x≠-l B.x >-1 C.x =- 1 D.x <- 1
3.据广东信息网消息,2006年第一季度,全省经济运行呈现平稳增长态势.初步核算,全省完成生产总值约为5206亿元,用科学记数法表示这个数为 ( )
A.5.206×102亿元 B.0.5206×103亿元 C.5.206× 103亿元 D.0.5206×104亿元
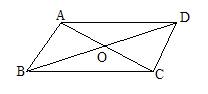
 4.如图所示,在□ABCD中,对角线AC、BD交于点O,
4.如图所示,在□ABCD中,对角线AC、BD交于点O,
下列式子中一定成立的是 ( )
A.AC⊥BD B.OA=0C
C.AC=BD D.A0=OD
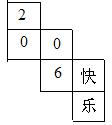
5.水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示,如图是一个正方体的表面展开图,若图中“2”在正方体的前面,则这个正方体的后面是 ( )
A.O B. 6 C.快 D.乐
二、填空题(本大题共5小题,每小题4分,共20分)请把下列各题的正确答案填写在横线上。
6.在数据1,2,3,1,2,2,4中,众数是
 7.分解因式2x2-4xy +2y2=
7.分解因式2x2-4xy +2y2=
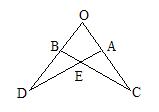
8.如图,若△OAD≌△OBC,且∠0=65°,∠C=20°,
则∠OAD= .
9.化简![]() =
.
=
.
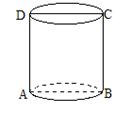
10.如图,已知圆柱体底面圆的半径为![]() ,高为2,AB、CD分别是两底面的直径,AD、BC是母线若一只小虫从A点出发,从侧面爬行到C点,则小虫爬行的最短D路线的长度是 (结果保留根式).
,高为2,AB、CD分别是两底面的直径,AD、BC是母线若一只小虫从A点出发,从侧面爬行到C点,则小虫爬行的最短D路线的长度是 (结果保留根式).
三、解答题(本大题共5小题,每小题6分,共30分)
11.求二次函数y=x2- 2x-1的顶点坐标及它与x轴的交点坐标.
12.按下列程序计算,把答案写在表格内:
![]()
(1)填写表格:
| 输入n | 3 | | —2 | —3 | … |
| 输出答案 | 1 | 1 | … |
(2)请将题中计算程序用代数式表达出来,并给予化简.
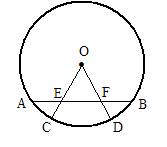 |
13.如图所示,AB是OD的弦,半径OC、OD分别交AB于点E、F,
且AE=BF,请你找出线段OE与OF的数量关系,并给予证明.
14.妞妞和她的爸爸玩“锤子、剪刀、布”游戏.每次用一只手可以出锤子、剪刀、布三种手势之一,规则是锤子赢剪刀、剪刀赢布、布赢锤子,若两人出相同手势,则算打平.
(1)你帮妞妞算算爸爸出“锤子”手势的概率是多少?
答:
(2)妞妞决定这次出“布”手势,妞妞赢的概率有多大?
 答:
答:
(3)妞妞和爸爸出相同手势的概率是多少?
答:
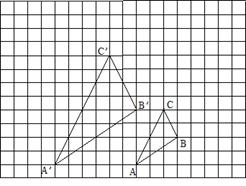
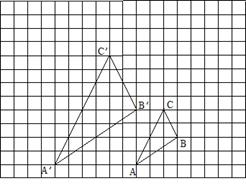
15.如图,图中的小方格都是边长为1的正方形, △ABC与△A′ B′ C′是关于点0为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
(1)画出位似中心点0;
(2)求出△ABC与△A′B′C′的位似比;
(3)以点0为位似中心,再画一个△A1B1C1,使它与△ABC的位似比等于1.5.
四、解答题(本大题共4小题。每小题7分。共28分)
16.为了了解学生参加体育活动的情况,学校对学生进行随机抽样调查,其中一个问题是“你
平均每天参加体育活动的时间是多少?”,共有4个选项:
A.1.5小时以上 B.1~1.5小时 C.0.5—1小时D.0.5小时以下
图1、2是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息,解答以下问题:
(1)本次一共调查了多少名学生?
(2)在图1中将选项B的部分补充完整;
(3)若该校有3000名学生,你估计全校可能有多少名学生平均每天参加体育活动的时间
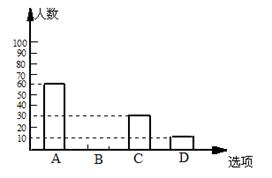 在0.5小时以下.
在0.5小时以下.
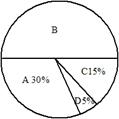 |
图1 图2
17.将一箱苹果分给若干个小朋友,若每位小朋友分5个苹果,则还剩12个苹果;若每位小朋友分8个苹果,则有—个小朋友分不到8个苹果.求这一箱苹果的个数与小朋友的人数.
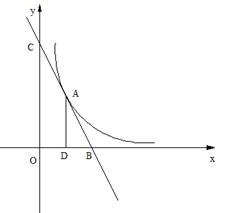 18.直线y=k1x+b与双曲线y=
18.直线y=k1x+b与双曲线y=![]() 只有—个交点A(1,2),且与x轴、y轴分别交于B,C 两点AD垂直平分OB,垂足为D,求直线、双曲线的解析式.
只有—个交点A(1,2),且与x轴、y轴分别交于B,C 两点AD垂直平分OB,垂足为D,求直线、双曲线的解析式.
19.已知:⊙O的半径是8,直线PA,PB为⊙O的切线,A、B两点为切点,
(1)当OP为何值时,∠APB=90°.
(2)若∠APB=50°,求AP的长度(结果保留三位有效数字).
(参考数据si50°=O.7660,cos50°=0.6428,tan50°=1.1918,sin25°=0.4226,
COS25°=0.9063,tan25°=O.4663)
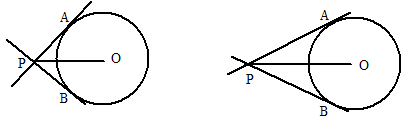 |
五、解答题(本大题共3小题,每小题9分,共27分)
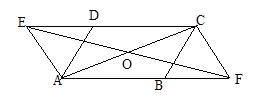
20.如图,在□ABCD中,∠DAB=60°,点E、F分别在CD、AB的延长线上,且AE=AD,CF=CB.
(1)求证:四边形AFCE是平行四边形.
(2)若去掉已知条件的“∠DAB=60°,上述的结论还成立吗?若成立,请写出证明过程;
 若不成立,请说明理由.
若不成立,请说明理由.
21.将一条长为20cm的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形.
(1)要使这两个正方形的面积之和等于17cm2,那么这段铁丝剪成两段后的长度分别是多少?
(2)两个正方形的面积之和可能等于12cm2吗? 若能,求出两段铁丝的长度;若不能,请说明理由.
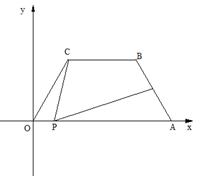
22.如图所示,在平面直角坐标中,四边形OABC是等腰梯形,BC∥OA,OA=7,AB=4,∠ COA=60°,点P为x轴上的—个动点,点P不与点0、点A重合.连结CP,过点P作PD交AB于点D.
(1)求点B的坐标;
(2)当点P运动什么位置时,△OCP为等腰三角形,求这时点P的坐标;
(3)当点P运动什么位置时,使得∠CPD=∠OAB,且![]() =
=![]() ,求这时点P的坐标。
,求这时点P的坐标。
初中毕业学业考试数学试卷参考答案
一、选择题(本大题共5小题,每小题3分,共15分)在每小题给出的四个选项中,只有一个是正确的,请将所选选项的字母写在题目后面的括号内。
1. ( A )
2. ( A )
3. ( C )
4. ( B )
5. ( B )
二、填空题(本大题共5小题,每小题4分,共20分)请把下列各题的正确答案填写在横线上。
6. 2
7. ![]()
8. 95° .
9. ![]() .
.
10.![]()
三、解答题(本大题共5小题,每小题6分,共30分)
11.
| 解法一(配方法):
∴ 顶点坐标为(1,-2) ………………3分 令Y=0,得 解得 ∴ 与X轴的交点坐标为( ………………6分 | 解法二(公式法): ∵a=1,b=-2,c=-1 ∴ ∴ 顶点坐标为(1,-2) ………………3分 (下同左) |
12.按下列程序计算,把答案写在表格内:
![]()
(1)填写表格: ………………4分
| 输入n | 3 | | —2 | —3 | … |
| 输出答案 | 1 | 1 | 1 | 1 | … |
 (2)请将题中计算程序用代数式表达出来,并给予化简.
(2)请将题中计算程序用代数式表达出来,并给予化简.
解:代数式为:![]() ………………5分
………………5分
化简结果为:1 ………………6分
13.如图所示,AB是OD的弦,半径OC、OD分别交AB于点E、F,且AE=BF,请你找出线段OE与OF的数量关系,并给予证明.
解:OE=OF, ………………2分
证明:连结OA,OB………………3分
∵ OA=OB
∴∠A=∠B ………………4分
又∵AE=BF
∴△OAE≌△OBF ………………5分
∴OE=OF ………………6分
14.妞妞和她的爸爸玩“锤子、剪刀、布”游戏.每次用一只手可以出锤子、剪刀、布三种手势之一,规则是锤子赢剪刀、剪刀赢布、布赢锤子,若两人出相同手势,则算打平.
(1)你帮妞妞算算爸爸出“锤子”手势的概率是多少?
答:![]() ………………2分
………………2分
(2)妞妞决定这次出“布”手势,妞妞赢的概率有多大?
答:![]() ………………4分
………………4分
(3)妞妞和爸爸出相同手势的概率是多少?
答:![]() ………………6分
………………6分
15.如图,图中的小方格都是边长为1的正方形, △ABC与△A′ B′ C′是关于点0为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
(1)画出位似中心点0;………………2分
(2)求出△ABC与△A′B′C′的位似比;
解:位似比为 1:2 ………………4分
(3)以点0为位似中心,再画一个△A1B1C1,使它与△ABC的位似比等于1.5.
………………6分
四、解答题(本大题共4小题。每小题7分。共28分)
16.为了了解学生参加体育活动的情况,学校对学生进行随机抽样调查,其中一个问题是“你
平均每天参加体育活动的时间是多少?”,共有4个选项:
A.1.5小时以上 B.1~1.5小时 C.0.5—1小时D.0.5小时以下
图1、2是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息,解答以下问题:
(1)本次一共调查了多少名学生?
解:200名 ………………3分
(2)在图1中将选项B的部分补充完整;………………5分
(3)若该校有3000名学生,你估计全校可能有多少名学生平均每天参加体育活动的时间
在0.5小时以下.
解:![]() 人 ………………7分
人 ………………7分
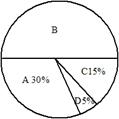
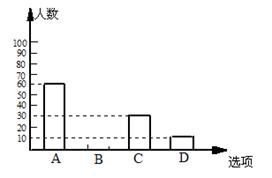
图1 图2
17.将一箱苹果分给若干个小朋友,若每位小朋友分5个苹果,则还剩12个苹果;若每位小朋友分8个苹果,则有—个小朋友分不到8个苹果.求这一箱苹果的个数与小朋友的人数.
解:设有x人, 则苹果有(![]() )个 ………………1分
)个 ………………1分
由题意, 得![]() ………………4分
………………4分
解得:![]() ………………5分
………………5分
∵ X为正整数
∴X=5或6 ………………6分
当X=5时,![]() 人
人
当X=6时,![]() 人
人
答:略 ………………7分
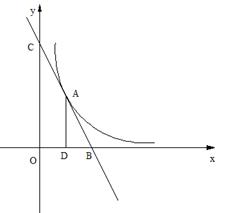 18.直线y=k1x+b与双曲线y=
18.直线y=k1x+b与双曲线y=![]() 只有—个交点A(1,2),且与x轴、y轴分别交于B,C 两点AD垂直平分OB,垂足为D,求直线、双曲线的解析式.
只有—个交点A(1,2),且与x轴、y轴分别交于B,C 两点AD垂直平分OB,垂足为D,求直线、双曲线的解析式.
解:
∵点A(1,2)在![]() 上 ………………1分
上 ………………1分
∴![]()
∴![]() ………………2分
………………2分
∴双曲线的解析式为![]() ………………3分
………………3分
∵AD垂直平分OB,
∴OD=1,OB=2
∴B(2,0) ………………4分
∵A(1,2),B(2,0)在直线![]() 上
上
∴ ![]() ………………5分
………………5分
解得![]() ………………6分
………………6分
∴直线解析式为![]() ………………7分
………………7分
19.已知:⊙O的半径是8,直线PA,PB为⊙O的切线,A、B两点为切点,
(1)当OP为何值时,∠APB=90°.
(2)若∠APB=50°,求AP的长度(结果保留三位有效数字).
(参考数据si50°=O.7660,cos50°=0.6428,tan50°=1.1918,sin25°=0.4226,
COS25°=0.9063,tan25°=O.4663)
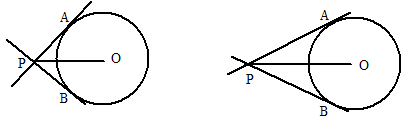 |
(1)解:连结OA ………………1分
∵PA,PB是⊙O的切线
∴∠PAO=90°,∠APO=∠BPO ………………2分
∵∠APB=90°
∴∠APO=45°
∴∠AOP=45°
∴OA=PA=8 ………………3分
∴OP=![]() ………………4分
………………4分
(2)解:连结OA
∵PA,PB是⊙O的切线
∴∠APO=∠BPO=![]() ∠APB=25° ………………5分
∠APB=25° ………………5分
∵![]() ………………6分
………………6分
∴![]() ………………7分
………………7分
五、解答题(本大题共3小题,每小题9分,共27分)
20.如图,在□ABCD中,∠DAB=60°,点E、F分别在CD、AB的延长线上,且AE=AD,CF=CB.
(1)求证:四边形AFCE是平行四边形.
(2)若去掉已知条件的“∠DAB=60°,上述的结论还成立吗?若成立,请写出证明过程;
 若不成立,请说明理由.
若不成立,请说明理由.
(1)证:∵四边形ABCD是平行四边形
∴DC∥AB,∠DCB=∠DAB=60°
∴∠ADE=∠CBF=60°
∵AE=AD,CF=CB
∴△AED,△CFB是正三角形
在![]() ABCD中,AD=BC,DC∥=AB
ABCD中,AD=BC,DC∥=AB
∴ED=BF ………………2分
∴ED+DC=BF+AB
即 EC=AF ………………3分
又∵DC∥AB
即EC∥AF
∴四边形AFCE是平行四边形 ………………4分
(2)上述结论还成立 ………………5分
证明:∵四边形ABCD是平行四边形
∴DC∥AB,∠DCB=∠DAB,AD=BC,DC∥=AB
∴∠ADE=∠CBF
∵AE=AD,CF=CB
∴∠AED=∠ADE,∠CFB=∠CBF
∴∠AED=∠CFB ………………6分
又∵AD=BC
∴△ADE≌△CBF ………………7分
∴ED=FB
∵DC=AB
∴ED+DC=FB+AB
即EC=FA ………………8分
∵DC∥AB
∴四边形EAFC是平行四边形 ………………9分
21.将一条长为20cm的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形.
(1)要使这两个正方形的面积之和等于17cm2,那么这段铁丝剪成两段后的长度分别是多少?
(2)两个正方形的面积之和可能等于12cm2吗? 若能,求出两段铁丝的长度;若不能,请说明理由.
(1)解:设剪成两段后其中一段为xcm,则另一段为(20-x)cm ………………1分
由题意得:![]() ………………3分
………………3分
解得:![]() ,
,![]() ………………4分
………………4分
当![]() 时,20-x=4
时,20-x=4
当![]() 时,20-x=16
时,20-x=16
答:(略) ………………5分
(2)不能 ………………6分
理由是:
![]() ………………7分
………………7分
整理得:![]()
∵ △=![]() ………………8分
………………8分
∴此方程无解 ………………9分
即不能剪成两段使得面积和为12cm2
22.如图所示,在平面直角坐标中,四边形OABC是等腰梯形,BC∥OA,OA=7,AB=4,∠ COA=60°,点P为x轴上的—个动点,点P不与点0、点A重合.连结CP,过点P作PD交AB于点D.
(1)求点B的坐标;
(2)当点P运动什么位置时,△OCP为等腰三角形,求这时点P的坐标;
(3)当点P运动什么位置时,使得∠CPD=∠OAB,且![]() =
=![]() ,求这时点P的坐标。
,求这时点P的坐标。
(1);过C作CD⊥OA于A,BE⊥OA于E ………………1分
则△OCD≌△ABE,四边形CDEB为矩形
 ∴OD=AE,CD=BE
∴OD=AE,CD=BE
∵OC=AB=4,∠COA=60°
∴CD=![]() ,OD=2 ………………2分
,OD=2 ………………2分
∴CB=DE=3
∴OE=OD+DE=5 ………………3分
∵BE=CD=![]()
∴B(5,![]() ) ………………4分
) ………………4分
(2)
∵∠COA=60°,△OCP为等腰三角形
∴△OCP是等边三角形
∴OP=OC=4 ………………5分
∴P(4,0)
即P运动到(4,0)时,△OCP为等腰三角形 ………………6分
(3)
∵∠CPD=∠OAB=∠COP=60°
∴∠OPC+∠DPA=120°
又∵∠PDA+∠DPA=120°
∴∠OPC=∠PDA
∵∠OCP=∠A=60°
∴△COP∽△PAD ………………7分
∴![]()
∵![]() ,AB=4
,AB=4
∴BD=![]()
∴AD=![]() ………………8分
………………8分
即 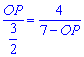
∴![]()
得OP=1或6
∴P点坐标为(1,0)或(6,0) ………………9分