初中毕业数学学业考试标准
数 学
一、考试指导思想
初中毕业数学学业考试是依据《全日制义务教育数学课程标准(实验稿)》(以下简称《数学课程标准》)进行的义务教育阶段数学学科的终结性考试。考试要有利于全面贯彻国家教育方针,推进素质教育;有利于体现九年义务教育的性质,全面提高教育质量;有利于数学课程改革,培养学生的创新精神和实践能力,减轻学生过重的课业负担,促进学生生动、活泼、主动地学习。
数学学业考试命题应当面向全体学生,根据学生的年龄特征、思维特点、数学背景和生活经验编制试题,使具有不同认知特点、不同数学发展程度的学生都能正常表现自己的学习状况,力求公正、客观、全面、准确地评价学生通过初中教育阶段的数学学习所获得的发展状况。
二、考试内容和要求
(一)考试内容
数学学业考试应以《数学课程标准》所规定的四大学习领域,即数与代数、空间与图形、统计与概率、实践与综合应用的内容为依据,主要考查基础知识与基本技能、数学活动过程、数学思考、解决问题能力、对数学的基本认识等。
1.关注基础知识与基本技能
了解数的意义,理解数和代数运算的意义、算理,能够合理地进行基本运算与估算;能够在实际情境中有效地使用代数运算、代数模型及相关概念解决问题。
能够借助不同的方法探索几何对象的有关性质;能够使用不同的方式表达几何对象的大小、位置与特征;能够在头脑里构建几何对象,进行几何图形的分解与组合,能对某些图形进行简单的变换;能够借助数学证明的方法确认数学命题的正确性。
正确理解数据的含义,能够结合实际需要有效地表达数据特征,会根据数据结果做合理的预测;了解概率的涵义,能够借助概率模型或通过设计活动解释一些事件发生的概率。
有条件的地区还应当考查学生能否使用计算器灵活地处理数值计算问题和从事有关探索规律的活动。
2. 关注“数学活动过程”
数学活动过程中所表现出来的思维方式、思维水平,对活动对象、相关知识与方法的理解深度;从事探究的意识、能力和信心等。能否通过观察、实验、归纳、类比等活动获得数学猜想,并寻求证明猜想的合理性;能否使用恰当的语言有条理地表达自已的数学思考过程。
3.关注“数学思考”
学生在数感与符号感、空间观念、统计意识、推理能力、应用数学的意识等方面的发展情况,其内容主要包括:
能用数来表达和交流信息;能够使用符号表达数量关系,并借助符号转换获得对事物的理解;能够观察到现实生活中的基本几何现象;能够运用图形形象地表达问题、借助直观进行思考与推理;能意识到做一个合理的决策需要借助统计活动去收集信息;面对数据时能对它的来源、处理方法和由此而得到的推测性结论做合理的质疑;能正确地认识生活中的一些确定或不确定现象;能从事基本的观察、分析、实验、猜想和推理的活动,并能够有条理地、清晰地阐述自已的观点。
4.关注“解决问题能力”
能从数学角度提出问题、理解问题、并综合运用数学知识解决问题;具有一定的解决问题的基本策略;能合乎逻辑地与他人交流;具有初步的反思意识。
5.关注“对数学的基本认识”
形成对数学内容统一性的认识(不同数学知识之间的联系、不同数学方法之间的相似性等);深化对数学与现实或其他学科知识之间联系的认识等等。
(二)考试要求
1.《数学课程标准》规定了初中数学的教学要求
(1)使学生获得适用未来社会生活和进一步发展所必需的重要数学知识,以及基本的数学思想方法和必要的应用技能;
(2)初步学会运用数学的思维方式观察、分析现实社会,解决日常生活和其他学科学习中的问题,增强应用数学的意识;
(3)体会数学与自然及人类社会的密切联系,了解数学的价值,增进对数学的理解和学好数学的信心;
(4)具有初步的创新精神和实践能力,在情感态度和一般能力方面都能得到充分发展。
这些教学要求是确定学业考试要求的重要依据。
2.《数学课程标准》阐述的教学要求具体分以下几个层次
知识技能要求:
(1)了解:能从具体事例中,知道或能举例说明对象的有关特征(或意义);能根据对象的特征,从具体情境中辨认出这一对象。
(2)理解:能描述对象特征和由来;能明确地阐述此对象与有关对象之间的区别和联系。
(3)掌握:能在理解的基础上,把对象运用到新的情境中去。
(4)灵活运用:能综合运用知识,灵活、合理地选择与运用有关的方法完成特定的数学任务。
过程性要求:
(5)经历(感受):在特定的数学活动中,获得一些初步的感受。
(6)体验(体会):参与特定的数学活动,在具体情境中初步认识对象的特征,获得一些经验。
(7)探索:主动参与特定的数学活动,通过观察、实验、推理等活动发现对象的某些特征或与其他对象的区别和联系。
这些要求从不同角度表明了数学学业考试要求的层次性。
(三)具体内容与考试要求细目列表
(表中“目标要求”栏中的序号和“(二)2.”中的规定一致)
| 具 体 内 容 | 知识技能要求 | 过程性要求 | ||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | ||
| 数 与 式 | 有理数的意义,用数轴上的点表示有理数 | √ | ||||||
| 相反数、绝对值的意义 | √ | |||||||
| 求相反数、绝对值,有理数的大小比较 | √ | |||||||
| 有理数加、减、乘、除、乘方及简单混合运算(三步为主),运用运算律进行简化运算 | √ | |||||||
| 运用有理数的运算解决简单问题 | √ | |||||||
| 对含有较大数字的信息作出合理解释 | √ | |||||||
| 平(立)方根的概念及其表示 | √ | |||||||
| 用平方运算求某些非负数的平方根,用立方运算求某些数的立方根,用计算器求平方根与立方根 | √ | |||||||
| 无理数与实数的概念、实数与数轴上的点的一一对应关系 | √ | |||||||
| 用有理数估计一个无理数的大致范围 | √ | |||||||
| 近似数与有效数字的概念 | √ | |||||||
| 用计算器进行近似计算,并按问题的要求对结果取近似值 | √ | |||||||
| 二次根式的概念及加、减、乘、除运算法则 | √ | |||||||
| 二次根式的简单四则运算(不要求分母有理化) | √ | |||||||
| 用字母表示数,列代数式表示简单数量关系 | √ | |||||||
| 代数式的实际意义与几何背景 | √ | |||||||
| 求代数式的值 | √ | |||||||
| 整数指数幂及其性质 | √ | |||||||
| 用科学记数法表示数(含计算器) | √ | |||||||
| 整式的概念(整式、单项式、多项式) | √ | |||||||
| 整式的加、减、乘(其中的多项式相乘仅指一次式相乘)运算 | √ | |||||||
| 乘法公式及计算 | √ | |||||||
| 因式分解的概念 | √ | |||||||
| 用提公因式法、公式法(直接用公式不超过2次)进行因式分解 | √ | |||||||
| 分式的概念 | √ | |||||||
| 约分、通分 | √ | |||||||
| 简单分式的运算(加、减、乘、除) | √ | |||||||
| 方程与不等式 | 方程(组)的解的检验 | √ | ||||||
| 估计方程的解 | √ | |||||||
| 一元一次方程及解法 | √ | |||||||
| 二元一次方程组及解法 | √ | |||||||
| 可化为一元一次方程的分式方程(方程中分式不超过2个)及解法 | √ | |||||||
| 一元二次方程及其解法 | √ | |||||||
| 根据具体问题中的数量关系列方程(组)并解决实际问题 | √ | |||||||
| 根据具体问题中的数量关系列不等式(组)并解决简单实际问题 | √ | |||||||
| 不等式的基本性质 | √ | √ | ||||||
| 解一元一次不等式(组) | √ | |||||||
| 用数轴表示一元一次不等式(组)的解集 | √ | |||||||
| 函 数 | 简单实际问题中的函数关系的分析 | √ | ||||||
| 具体问题中的数量关系及变化规律 | √ | |||||||
| 常量、变量的意义 | √ | |||||||
| 函数的概念及三种表示法 | √ | |||||||
| 简单函数的自变量取值范围,函数值 | √ | |||||||
| 使用适当的函数表示法,刻画实际问题中变量之间的关系 | √ | |||||||
| 一次函数及表达式 | √ | √ | ||||||
| 一次函数的图象及性质 | √ | √ | ||||||
| 正比例函数 | √ | |||||||
| 用图象法求二元一次方程组的近似解 | √ | |||||||
| 用一次函数解决实际问题 | √ | |||||||
| 反比例函数及表达式 | √ | √ | ||||||
| 反比例函数的图象及性质 | √ | √ | ||||||
| 用反比例函数解决实际问题 | √ | |||||||
| 二次函数及表达式 | √ | √ | ||||||
| 二次函数的图象及性质 | √ | |||||||
| 确定二次函数图象的顶点、开口方向及其对称轴 | √ | |||||||
| 用二次函数解决简单实际问题 | √ | |||||||
| 用二次函数图象求一元二次方程的近似解 | √ | |||||||
| 图形的认识 | 点、线、面 | √ | ||||||
| 角的大小比较、估计,角的和与差的计算 | √ | |||||||
| 角的单位换算 | √ | |||||||
| 角平分线及其性质 | √ | |||||||
| 补角、余角、对顶角 | √ | |||||||
| 垂直、垂线段概念及性质,点到直线的距离 | √ | √ | ||||||
| 线段垂直平分线及性质 | √ | |||||||
| 平行线的性质 | √ | √ | ||||||
| 平行线间的距离 | √ | √ | ||||||
| 画平行线 | √ | |||||||
| 三角形的有关概念 | √ | |||||||
| 画任意三角形的角平分线、中线、高 | √ | |||||||
| 三角形的稳定性 | √ | |||||||
| 三角形中位线的性质 | √ | √ | ||||||
| 全等三角形的概念 | √ | |||||||
| 两个三角形全等的条件 | √ | √ | ||||||
| 等腰三角形的有关概念 | √ | |||||||
| 等腰三角形的性质及判定 | √ | √ | ||||||
| 直角三角形的概念 | √ | |||||||
| 直角三角形的性质及判定 | √ | √ | ||||||
| 勾股定理及其逆定理的运用 | √ | √ | ||||||
| 多边形的内角和与外角和公式 | √ | √ | ||||||
| 正多边形的概念 | √ | |||||||
| 平行四边形、矩形、菱形、正方形、梯形的概念 | √ | |||||||
| 平行四边形的性质及判定 | √ | √ | ||||||
| 矩形、菱形、正方形的性质及判定 | √ | √ | ||||||
| 等腰梯形的有关性质和判定 | √ | √ | ||||||
| 线段、矩形、平行四边形、三角形的重心及其物理意义 | √ | √ | ||||||
| 平面图形的镶嵌、镶嵌的简单设计 | √ | |||||||
| 图形的认识 | 圆及其有关概念 | √ | ||||||
| 弧、弦、圆心角的关系 | √ | |||||||
| 点与圆、直线与圆、圆与圆的位置关系 | √ | √ | ||||||
| 圆周角与圆心角的关系,直径所对圆周角的特征 | √ | |||||||
| 三角形的内心与外心 | √ | |||||||
| 切线的概念 | √ | |||||||
| 切线的性质与判定 | √ | √ | ||||||
| 弧长公式、扇形面积公式 | √ | |||||||
| 圆锥的侧面积和全面积 | √ | |||||||
| 基本作图 | √ | |||||||
| 利用基本作图作三角形 | √ | |||||||
| 过平面上的点作圆 | √ | √ | ||||||
| 尺规作图的步骤(已知、求作、作法) | √ | |||||||
| 图形与变换 | 基本几何体的三视图 | √ | ||||||
| 基本几何体与其三视图、展开图之间的关系 | √ | |||||||
| 直棱柱、圆锥的侧面展开图 | √ | |||||||
| 视点、视角及盲区的涵义,及其在简单的平面图和立体图中的表示 | √ | |||||||
| 物体阴影的形成,根据光线的方向辨认实物的阴影 | √ | |||||||
| 中心投影和平行投影 | √ | |||||||
| 轴对称的基本性质 | √ | √ | ||||||
| 利用轴对称作图,简单图形间的轴对称关系 | √ | √ | ||||||
| 基本图形的轴对称性及其相关性质 | √ | |||||||
| 轴对称图形的欣赏与设计 | √ | |||||||
| 平移的概念、平移的基本性质 | √ | √ | ||||||
| 利用平移作图,图形的欣赏与设计 | √ | |||||||
| 旋转的概念、旋转的基本性质 | √ | √ | ||||||
| 平行四边形、圆的中心对称性 | √ | |||||||
| 利用旋转作图 | √ | |||||||
| 图形之间的变换关系(轴对称、平移与旋转) | √ | |||||||
| 用轴对称、平移和旋转的组合进行图案设计 | √ | |||||||
| 图形与变换 | 比、成比例线段、黄金分割 | √ | ||||||
| 图形的相似、相似图形的性质 | √ | √ | ||||||
| 两个三角形相似的性质及判定、直角三角形相似的判定 | √ | √ | ||||||
| 位似及应用 | √ | |||||||
| 相似的应用 | √ | |||||||
| 锐角三角函数(正弦、余弦、正切) | √ | |||||||
| 特殊角(30°、45°、60°)的三角函数值 | √ | |||||||
| 使用计算器求已知锐角三角函数的值,由已知三角函数值求它对应的锐角 | √ | |||||||
| 三角函数的简单应用 | √ | |||||||
| 图形与坐标 | 平面直角坐标系;在给定的直角坐标系中,根据坐标描出点的位置,由点的位置写出它的坐标 | √ | ||||||
| 建立适当的直角坐标系描述物体的位置 | √ | |||||||
| 图形的变换与坐标的变化 | √ | |||||||
| 用不同的方式确定物体的位置 | √ | |||||||
| 图形与证明 | 证明的必要性 | √ | ||||||
| 定义、命题、定理、互逆命题 | √ | |||||||
| 反例的作用及反例的应用 | √ | |||||||
| 反证法的含义 | √ | |||||||
| 证明的格式及依据 | √ | |||||||
| 全等三角形的性质定理和判定定理 | √ | |||||||
| 平行线的性质定理和判定定理 | √ | |||||||
| 三角形的内角和定理及推论 | √ | |||||||
| 直角三角形全等的判定定理 | √ | |||||||
| 角平分线性质定理及逆定理 | √ | |||||||
| 垂直平分线性质定理及逆定理 | √ | |||||||
| 三角形中位线定理 | √ | |||||||
| 等腰三角形、等边三角形、直角三角形性质与判定定理 | √ | |||||||
| 平行四边形、矩形、菱形、正方形、等腰梯形的性质和判定定理 | √ | |||||||
| 统 计 | 数据的收集与整理,用计算器处理较复杂的统计数据 | √ | ||||||
| 总体、个体、样本的概念 | √ | √ | ||||||
| 扇形统计图 | √ | |||||||
| 选择合适的统计量(平均数、中位数、众数)表示数据的集中程度 | √ | |||||||
| 加权平均数 | √ | |||||||
| 一组数据的离散程度的表示;计算极差和方差,用它们表示一组数据的离散程度 | √ | √ | ||||||
| 频数、频率的概念 | √ | |||||||
| 列频数分布表、画频数分布直方图和频数折线图,并解决简单实际问题 | √ | |||||||
| 频数分布的意义和作用 | √ | |||||||
| 用样本估计总体的思想,用样本平均数、方差估计总体的平均数和方差 | √ | |||||||
| 根据统计结果作出合理的判断和预测,统计对决策的作用 | √ | |||||||
| 根据问题查找资料,获取数据信息,解决简单的实际问题 | √ | |||||||
| 概 率 | 概率的意义 | √ | ||||||
| 用列举法求简单事件的概率 | √ | |||||||
| 通过实验,获取事件发生的频率,大量重复实验时频率可作为事件发生概率的估计值 | √ | |||||||
| 通过实验丰富对概率的认识,并解决一些实际问题 | √ | |||||||
| 课题学习 | “问题情境——建立模型——求解——解释与应用”的基本过程 | √ | ||||||
| 数学知识之间的内在联系,对数学的整体认识 | √ | |||||||
| 获得一些研究问题的方法和经验,发展思维,加深理解相关知识 | √ | |||||||
| 通过获得成功的体验和克服困难的经历,增进应用数学的自信心 | √ | |||||||
三、试卷结构
(一)试卷结构
(1)填空题:8-10小题,约占20%;
(2)选择题:8-10小题,约占20%;
(3)解答题:8-10个小题,约占60%,解答题包括计算题、证明题、应用性问题、实践操作题、拓展探究题等不同形式。
(二)试题难度
试卷整体难度控制在0.65-0.80之间,容易题约占70%、稍难题约占15%、较难题约占15%。
(三)试题比例
1. 各能力层级试题比例:了解约占10%,理解约占20%,掌握约占60%,灵活运用占10%.
2. 各知识板块试题比例:数与代数约占50%,空间与图形约35%,统计与概率约占15%,考试内容覆盖面要求达到《课程标准》规定内容的80%。
四、题型示例
(一)选择题
例1 某地今年1月1日至4日每天的最高气温与最低气温如下表:
| 日 期 | 1月1日 | 1月2日 | 1月3日 | 1月4日 |
| 最高气温 | 5℃ | 4℃ | 0℃ | 4℃ |
| 最低气温 | 0℃ | -2℃ | -4℃ | -3℃ |
其中温差最大的是( )
A、1月1日 B、1月2日 C、 1月3日 D、1月4日
答案:D
 例2 如图,P1、P2、P3是函数y=
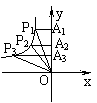
例2 如图,P1、P2、P3是函数y=![]() (k<0,x<0)图象上三点,过这三点分别作y轴的垂线,得到三个三角形P1A1O、P2A2O、P3A3O,它们的面积分别是S1、S2、S3,则( )
(k<0,x<0)图象上三点,过这三点分别作y轴的垂线,得到三个三角形P1A1O、P2A2O、P3A3O,它们的面积分别是S1、S2、S3,则( )
A、S1<S2<S3 B、S2<S1<S3
C、S1<S3<S2 D、S1=S2=S3
答案:D
 例3
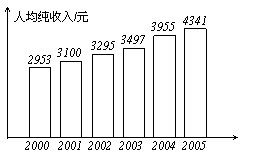
2006年1月5日《长江日报》报道:“十五”期间,某市城乡居民收入不断增长,其中农村居民人均纯收入由2000年的2953元增加到2005年的4341元。右图是该市2000年~2005年农村居民人均纯收入的统计图。根据统计图提供的信息判断:与上一年相比,农村居民人均纯收入增加最多的年份是( )
例3
2006年1月5日《长江日报》报道:“十五”期间,某市城乡居民收入不断增长,其中农村居民人均纯收入由2000年的2953元增加到2005年的4341元。右图是该市2000年~2005年农村居民人均纯收入的统计图。根据统计图提供的信息判断:与上一年相比,农村居民人均纯收入增加最多的年份是( )
|
C、2004 D、2005
答案:C
 例4 如图,用半径R=3cm,r=2cm的钢球测量口小内大的内孔的直径D。测得钢球顶点与孔口平面的距离分别为a=4cm,b=2cm,则内孔直径D的大小为( )
例4 如图,用半径R=3cm,r=2cm的钢球测量口小内大的内孔的直径D。测得钢球顶点与孔口平面的距离分别为a=4cm,b=2cm,则内孔直径D的大小为( )
A、9cm B、8cm
C、7cm D、6cm
答案:A
(二)填空题
 例5 1883年,康托尔构造的这个分形,称作康托尔集.从数轴上单位长度线段开始,康托尔取走其中间三分之一而达到第一阶段;然后从每一个余下的三分之一线段中取走其中间三分之一而达到第二阶段.无限地重复这一过程,余下的无穷点集就称做康托尔集。下图是康托尔集的最初几个阶段,当达到第八个阶段时,余下的所有线段的长度之和为 .
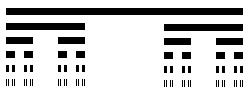
例5 1883年,康托尔构造的这个分形,称作康托尔集.从数轴上单位长度线段开始,康托尔取走其中间三分之一而达到第一阶段;然后从每一个余下的三分之一线段中取走其中间三分之一而达到第二阶段.无限地重复这一过程,余下的无穷点集就称做康托尔集。下图是康托尔集的最初几个阶段,当达到第八个阶段时,余下的所有线段的长度之和为 .
 答案:
答案:![]() (或0.039)
(或0.039)
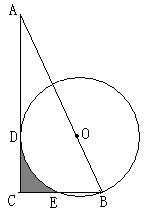
例6 如图,Rt△ABC中,∠C=90°,∠A=30°,点O在斜边AB上,半径为2的⊙O过点B,切AC边于点D,交BC边于点E。则由线段CD、CE及弧DE围成的阴影部分的面积为 .
答案:![]()
(三)解答题
 例7
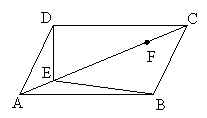
如图,在平行四边形ABCD中,点E、F在对角线AC上,且AE=CF,请你以F为一个端点和图中已标明字母的某一点连成一条线段,猜想并证明它和图中已有的某一条线段相等.(只须证明一组线段相等)
例7
如图,在平行四边形ABCD中,点E、F在对角线AC上,且AE=CF,请你以F为一个端点和图中已标明字母的某一点连成一条线段,猜想并证明它和图中已有的某一条线段相等.(只须证明一组线段相等)
(1)连结 ;
(2)猜想 ;
(3)证明:
答案:(1)BF;(2)DE![]() BF;(3)略.
BF;(3)略.
例8 农科所向农民推荐渝江Ⅰ号和渝江Ⅱ号两种新型良种稻谷。在田间管理和土质相同的条件下,Ⅱ号稻谷单位面积的产量比Ⅰ号稻谷低20%,但Ⅱ号稻谷的米质好,价格比Ⅰ号高。已知Ⅰ号稻谷国家的收购价是1.6元/千克.
(1)当Ⅱ号稻谷的国家收购价是多少时,在田间管理、土质和面积相同的两块田里分别种植Ⅰ号、Ⅱ号稻谷的收益相同?
(2)去年小王在土质、面积相同的两块田里分别种植Ⅰ号、Ⅱ号稻谷,且进行了相同的田间管理,收获后,小王把稻谷全部卖给国家。卖给国家时,Ⅱ号稻谷的国家收购价定为2.2元/千克,Ⅰ号稻谷国家的收购价未变,这样小王卖Ⅱ号稻谷比卖Ⅰ号稻谷多收入1040元,那么小王去年卖给国家的稻谷共有多少千克?
答案:(1)2元/千克;(2)11700千克
例9 某校有A、B两个餐厅,甲、乙、丙三名学生各自随机选择其中的一个餐厅用餐.
(1)求甲、乙、丙三名学生在同一个餐厅用餐的概率;
(2)求甲、乙、丙三名学生中至少有一人在B餐厅用餐的概率.
答案:(1)![]() ;(2)
;(2)![]() .
.
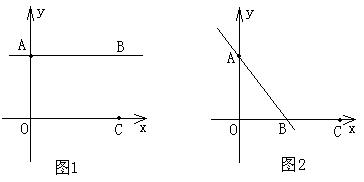
例10 在平面直角坐标系中,A点的坐标为(0,4),C点的坐标为(10,0)。
(1)如图1,若直线AB∥OC,AB上有一动点P,当P点的坐标为 时,有PO=PC;
(2)如图2,若直线AB与OC不平行,在过点A的直线y=-x+4上是否存在点P,使∠OPC=90°?若有这样的点P,求出它的坐标;若没有,请简要说明理由。
 |
(3)若点P在直线y=kx+4上移动时,只存在一个点P使∠OPC=90°,试求出此时k为多少?
答案:(1)(5,4);(2)存在,(1,3)和(8,-4);(3)![]()