初中毕业数学第一轮复习考试
数 学 试 题
注意事项：本卷考试时间为120分钟，满分150分. 卷中除要求近似计算的按要求给出近似结果外，其余结果均应给出精确结果.
一、选择题（本大题共7小题，每题3分，共21分．在每题所给出的四个选项中，只有一项符合题意．把所选项前的字母代号填在题后的括号内．相信你一定会选对！）
1．如果a与－2互为倒数，那么a是（ ）．
A．-2
B．-
C．
D．2
2．若反比例函数
的图象经过点A（2，m），则m的值是（ ）．
A．
B．
C．
D．
3．已知α为等边三角形的一个内角，则cosα等于（ ）．
A．
B．
C．
D．
4．教练组对运动员正式比赛前的5次训练成绩进行分析，判断谁的成绩更加稳定，一般需要考察这5次成绩的（ ）．
A．平均数或中位数 B．众数或频率
C．方差或极差 D．频数或众数
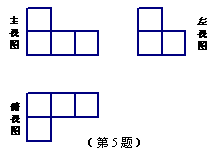
5．如图，是一个由若干个相同的小正方体组成的几何体的三视图，则组成这个几何体的小正方体的个数是（ ）．
A．4个 B．5个
C．6个 D．7个
6．根据下列表格的对应值：
| x | 3.23 | 3.24 | 3.25 | 3.26 |
| ax2+bx+c | －0.06 | －0.02 | 0.03 | 0.09 |
判断方程ax2+bx+c＝0（a≠0，a，b，c为常数）一个解x
的范围是（ ）．
A．3＜x＜3.23 B．3.23＜x＜3.24
C．3.24＜x＜3.25 D．3.25＜x＜3.26
www
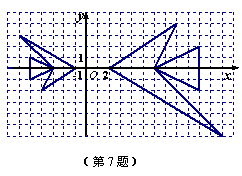
7．某学习小组在讨论“变化的鱼”时，知道右图中的大鱼与小鱼是位似图形，若小鱼上的点P（a，b）对应大鱼上的点Q，则点Q的坐标为（ ）．
A．（－2a，－2b） B．（－a，－2b）
C．（－2b，－2a） D．（－2a，－b）
二、填空题（本大题共10空，每题4分，共40分. 请把结果直接填在题中的横线上. 只要你理解概念，仔细运算，积极思考，相信你一定会填对的！）
8．（1）－的相反数是___________，16的算术平方根是___________.
（2）分解因式x2－4x＋4＝____________.
9．国务院总理温家宝3月5日在十届人大四次会议上作政府报告时说，2005年我国社会主义现代化事业取得显著成就，全年国内生产总值达到18.23万亿元，将这一数字用科学记数表示为______________亿元.
10．写出一个图象位于第二象限与第四象限的反比例函数解析式：___________________.
11．比较大小：（1）－3 －4；（2）
．
12．用字母表示图中阴影部分的面积为 ．
13．函数y＝中，自变量x的取值范围是___________；
函数y＝中，自变量x的取值范围是___________.
14．某商店销售一批服装，每件售价150元，打8折后，仍可获利20%，设这种服装的成本价为
元，则x满足的方程是
．
15．如图，PA、PB是⊙O的切线，A、B是切点，
∠ACB=65°,则∠APB= 度.
16．在地面上某一点周围有a个正三角形、b个正十二边形（a、b
均不为0），恰能铺满地面，则a＋b＝___________.
17．用两块大小相同的等腰直角三角形纸片做拼图游戏，则下列图形：
①平行四边形（不包括矩形、菱形、正方形）；②矩形（不包括正方形）；③正方形；④等边三角形；⑤等腰直角三角形，其中一定能拼成的图形是 ．
（只填序号）
三、解答题（本大题共9小题，满分89分．只要你认真思考，仔细运算，一定会解答正确的!）
18．（本题满分8分）（1）计算：(－2)3＋(1＋sin30º)0＋3－1×6
（2）先化简，再求值：
，其中m＝－2．
19．（本题满分8分）不透明的口袋里装有白、黄、蓝三种颜色的乒乓球（除颜色外其余都相同），其中白球有2个，黄球有1个，现从中任意摸出一个是白球的概率为.
（1）试求袋中蓝球的个数.
（2）第一次任意摸一个球（不放回），第二次再摸一个球，请用画树状图或列表格法，求两次摸到都是白球的概率.
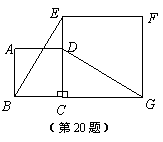
20．（本题满分8分）如图，正方形ABCD的边CD在正方形
ECGF的边CE上，连结BE、DG．
（1）观察猜想BE与DG之间的大小关系，并证明你的结论．
（2）图中是否存在通过旋转能够互相重合的两个三角形？若
存在，请说出旋转过程；若不存在，请说明理由．
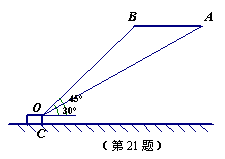21．（本题满分9分）如图，一架飞机以每小时900千米的速度水平飞行，某个时刻，从地面控制塔O（塔高300m）观测到飞机在A处的仰角为30°，5分钟后测得飞机在B处的仰角为45°，试确定飞机的飞行高度．（
，结果精确到1km）
22．（本题满分10分）某校科技夏令营的学生在3位老师的带领下，准备赴北京大学参观，体验大学生活．现有两家旅行社前来洽谈，报价均为每人2000元，且各有优惠．希望旅行社表示：带队老师免费，学生按8折收费；青春旅行社表示师生一律按7折收费．经核算发现，参加两家旅行社的实际费用正好相等．
（1）该校参加科技夏令营的学生共有多少人？
（2）如果又增加了部分学生，学校应选择哪家旅行社？为什么？
23．（本题满分10分）我们知道：顶点在圆上，并且两边都和圆相交的角叫做圆周角，一条弧所对的圆周角的度数等于它所对的圆心角度数的一半．类似地，我们定义：顶点在圆外，并且两边都和圆相交的角叫做圆外角．
（1）判断：图中有没有圆外角？如果有，请用字母表示出来．
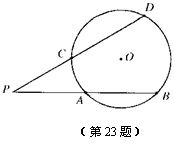（2）运用所学的数学知识，探究：圆外角的度数与它所夹的弧所对的圆心角的度数有什么关系？将你的发现，用文字表述出来，并说明理由．
24．（本题满分12分）如图，二次函数
（m<4）的图象与轴相交于点
A、B两点．
（1）求点A、B的坐标（可用含字母
的代数式表示）；
（2）如果这个二次函数的图象与反比例函数
的图象相交于点C，且
∠BAC的余弦值为
，求这个二次函数的解析式．
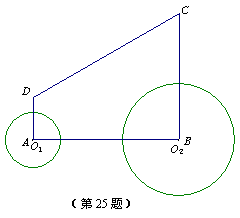25．（本题满分12分）如图，直角梯形ABCD中，AD∥BC，∠A＝90o，∠C＝60°，AD＝3cm，BC＝9cm．⊙O1的圆心O1从点A开始沿折线A—D—C以1cm/s的速度向点C运动，⊙O2的圆心O2从点B开始沿BA边以
cm/s的速度向点A运动，⊙O1半径为2cm，⊙O2的半径为4cm，若O1、O2分别从点A、点B同时出发，运动的时间为ts
（1）请求出⊙O2与腰CD相切时t的值；
（2）在0s＜t≤3s范围内，当t为何值时，⊙O1与⊙O2外切？
26．（本题满分12分）如图，一次函数y＝x＋m图象过点A（1，0），交y轴于点B，C为y轴负半轴上一点，且BC＝2OB，过A、C两点的抛物线交直线AB于点D，且CD∥x轴.
（1）求这条抛物线的解析式；
（2）观察图象，写出使一次函数值小于二次函数值时x的取值范围；
（3）在题中的抛物线上是否存在一点M，使得∠ADM为直角？若存在，求出点M的坐标；若不存在，请说明理由.
数学试卷参考答案及评分标准
一、选择题（每小题3分，共21分）
BCACB CA
二、填空题（每小题4分，共40分）
1．（1），4（2）(x－2)2； 9．1.823×105；10．答案不唯一，如y＝－等等；11．＞，＞12．
13．x≥3 ，x≠1；14．150×80%－x＝20%x 15．50 16．3； 17．①、③、⑤
三、解下列各题（本大题共9小题，满分89分）
18．（1）解：原式＝－8＋1＋2………………2分
＝－5………………………………4分
（2）解：
………………1分
＝
………………2分
＝
．………………3分
当m＝－2时，原式＝
．………………4分
19．（1）设蓝球个数为x个 ……1分
则由题意得＝ 解得 x＝1，即蓝球有1个 ……3分
（2）数状图或列表正确……4分
两次摸到都是白球的概率 ＝ ……7分 ＝……8分
20．解：（1）BE＝DG．………………2分
证明：∵四边形ABCD和四边形ECGF都是正方形，
∴BC＝DC，EC＝GC，∠BCE＝∠DCG＝90°．………………4分
∴△BCE≌△DCG．………………6分
∴BE＝DG．
（2）存在，它们是Rt△BCE和Rt△DCG．将Rt△BCE绕点C顺时针旋转90°，可与Rt△DCG完全重合．………………8分
21．解：AB＝
＝75（km）．………2分
过点O作OD⊥AB，垂足为D．………………3分
设OD＝xkm，在Rt△OBD中，∵∠OBD＝45°，
∴BD＝OD＝xkm．……………4分
在Rt△OAD中，AD＝AB+ BD＝(x+75) km，∠AOD＝60°，
∵tan∠AOD＝
，∴
．………………6分
解得x≈102.5（km）．
∴CD＝ OD +OC ＝102.5+0.3≈103（km）．………………8分
答：飞机的飞行高度约为103 km．………………9分
22．解：（1）设共有学生x人，希望旅行社费用为y1元，青春旅行社费用为y2元．
……………1分
根据题意得：
，即
；
，即
．
当y1＝y2时，即1600x＝1400x＋4200，………………5分
解得x＝21．………………7分
所以该校参加科技夏令营的学生共有21人．………………8分
（2）y1－y2＝200 x－4200．当x＞21时，y1－y2＞0，即y1＞y2．
所以如果增加部分学生，学校应选择青春旅行社．………………10分
23．解：（1）∠DPB是圆外角；………………2分
（2）圆外角的度数等于它所夹的弧所对的圆心角的度数的差的一半．………………5分
理由如下：连结DA，OA，OB，OC，OD，则
∵∠BAD＝∠BOD，∠ADC＝∠AOC，
∴∠BAD－∠ADC＝∠BOD－∠AOC．………………8分
∵∠DPB＝∠BAD－∠ADC，∴∠DPB＝∠BOD－∠AOC．………………10分
24．解：（1）当
，
，……………………………… 1分
，
．…………………………… 2分
∵
，∴A（–4，0），B（
，0）………………………………1分
（2）
过点C作CD⊥
轴，垂足为D，
cos∠BAC
,设AD=4k,AC=5k,
则CD=3k.
……………………1分
∵OA=4,∴OD=4k–4, 点C(4k–4,3k) . …………………………………1分
∵点C在反比例函数的图象上，∴
. ………………1分
. ……………………………1分
∴C(2，
).……………………（1分） ∵点C在二次函数的图象上，
∴
，………（1分） ∴
………………1分
∴二次函数的解析式为
. ……………………………1分
25．解：（1）如图所示，设点O2运动到点E处时，⊙O2与腰CD相切．
过点E作EF⊥DC，垂足为F，则EF＝4cm．………………1分
方法一，作EG∥BC，交DC于G，作GH⊥BC，垂足为H．
通过解直角三角形，求得EB＝GH＝
cm．………………5分
所以t＝（
）秒．………………6分
方法二，延长EA、FD交于点P．通过相似三角形，也可求出EB长．
方法三，连结ED、EC，根据面积关系，列出含有t的方程，直接求t．
（2）由于0s<t≤3s，所以，点O1在边AD上．………………7分
如图所示，连结O1O2，则O1O2＝6cm．………………8分
由勾股定理得，
，即
．………………10分
解得t1＝3，t2＝6（不合题意，舍去）．………………11分
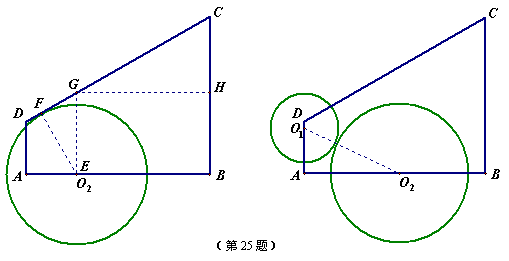所以，经过3秒，⊙O1与⊙O2外切．………………12分
26．（1）把点A（1，0）代入y＝x＋m得m＝－1， ∴y＝x－1 ∴点B坐标为（0，－1） …1分
∵BC＝2OB， OB＝1， ∴ BC＝2 ∴OC＝3 ∴ C点坐标为（0，－3）……2分
又CD∥x轴，∴点D的纵坐标为－3 代入y＝x－1得x＝－2，∴点D的坐标为（－2，－3）
设抛物线的解析式为y＝ax2＋bx＋c，
由题意得解得
∴ y＝x2＋2x－3 ……4分
（2）x＜－2 或x＞1 ……6分
（3）∵BC＝CD＝2 , 且 CD∥x轴，∴△BCD 为等腰直角三角形，∠BCD＝90°……8分
又 抛物线顶点为 E（－1,－4），且E到CD的距离为1
∴∠EDC＝45° ∴∠EDA＝90°……10分
∴存在点M（－1,－4 ）（即抛物线顶点E）使得∠ADM＝90°……12分
备注：第2小题过点D作AD的垂线交抛物线于点M也可求解，相应给分.