初中数学总复习反比例函数

初中数学总复习（14）反比例函数

〖考试内容〗

反比例函数及其图象.

〖考试要求〗

①理解反比例函数的意义，能根据已知条件确定反比例函数表达式.

②能画出反比例函数的图象，根据图象和解析式理解其性质（>0或<0时，图象的变化）.

③能用反比例函数解决某些实际问题.

〖考点复习〗

1．反比例函数表达式

[例1]如果反比例函数的图象经过点（，），那么的值是（　）

 A、－12　 B、12  C、  D、

2．反比例函数的图象及性质

[例2] ①写出一个图象位于一、三角限的反比例函数表达式 　　　　　　　 

②（2005深圳）函数y=（k≠0）的图象过点（2，-2），则此函数的图象在平面直角坐标系中的（　）

A、第一、三象限　　B、第三、四象限

C、A、第一、二象限　D、第二、四象限

[例3] 8、若M、N、P三点都在函数（ｋ＜0）的图象上，则的大小关系为（　）

A、＞＞　　B、＞＞　　C、＞＞　D、＞＞　

3．反比例函数与一次函数

[例4] 13.点P既在反比例函数的图像上，又在一次函数的图像上，则P点的坐标是___________.

4．反比例函数的运用

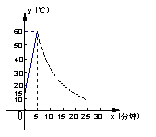[例5] （2005四川）制作一种产品，需先将材料加热达到60℃后，再进行操作．设该材料温度为y（℃），从加热开始计算的时间为x（分钟）．据了解，设该材料加热时，温度y与时间x成一次函数关系；停止加热进行操作时，温度y与时间x成反比例关系（如图）．已知该材料在操作加工前的温度为15℃，加热5分钟后温度达到60℃．

（1）分别求出将材料加热和停止加热进行操作时，y与x的函数关系式；

（2）根据工艺要求，当材料的温度低于15℃时，须停止操作，那么从开始加热到停止操作，共经历了多少时间？

〖考题训练〗

1．已知正比例函数与反比例函数的图象都经过点(2，1).求这两个函数关系式.

2．反比例函数的图象经过点（2，5），若点（1，n）在反比例函数的图象上，则n等于（　　 ）

A、10　　 B、5　　 C、2　　D、

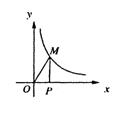
3．反比例函数y= (k>0)在第一象限内的图象如图，点M是图象上一点，MP垂直x轴于点P，如果△MOP的面积为1，那么k的值是(　)

(A) 1　　　(B) 2　　  (C) 4 　　　(D)

4． 任意写出一个图象经过二、四象限的反比例函数的解析式:__________

5．已知反比例函数，其图象在第一、第三象限内，则k的值可为　　　。（写出满足条件的一个k的值即可）

6．(2004河北) 在同一直角坐标系中，函数y=kx-k与(k≠0)的图象大致是（　 ）

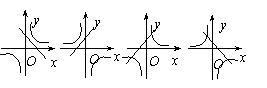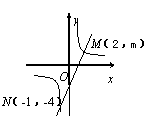　　A、　　　B、　　　 C、　　　　D、

7．如图，一次函数的图象与反比例函数的图象交于M、N两点.

（1）求反比例函数和一次函数的解析式；

（2）根据图象写出使反比例函数的值大于一次函数的值的x的取值范围.

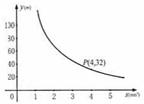8．你吃过拉面吗？实际上在做拉面的过程中就渗透着数学知识：一定体积的面团做成拉面，面条的总长度y(m)是面条的粗细(横截面积)s(mm²)的反比例函数，其图象如图所示。

（1）写出y与s的函数关系式；

（2）求当面条粗1.6mm²时，面条的总长度是多少米？

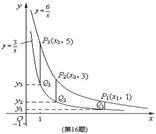
9．　两个反比例函数，在第一象限内的图象如图所示, 点P₁，P₂，P₃，…，P_{2 005}在反比例函数图象上，它们的横坐标分别是x₁，x₂，x₃，…，x_{2 005}，纵坐标分别是1，3，5，…，共2 005个连续奇数，过点P₁， P₂，P₃，…，P_{2 005}分别作y轴的平行线，与的图象交点依次是Q₁（x₁，y₁），Q₂（x₂，y₂），Q₃（x₃，y₃），…，Q_{2 005}（x_{2 005}，y_{2 005}），则y_{2 005}=　 　　　．

〖课后作业〗

（14）反比例函数

1．反比例函数y= -的图象位于（　）

　A、第一、二象限　　　B、第一、三象限

　C、第二、三象限　　　D、第二、四象限

2．（2005资阳）已知正比例函数y=k₁x(k₁≠0)与反比例函数y=(k₂≠0)的图象有一个交点的坐标为(-2，-1)，则它的另一个交点的坐标是

A、(2，1) B、(-2，-1) C、(-2，1) D、(2，-1)

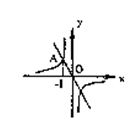3．如图，反比例函数与直线相交于点A，A点的横坐标为－1，则此反比例函数的解析式为（　　　　）

A、B、

C、 D、　　　　

4．反比例函数的图象经过点A(2，3)，

⑴求这个函数的解析式；

⑵请判断点B(1，6)是否在这个反比例函数的图象上，并说明理由。