（23）图形与证明
（1）了解证明的含义
〖考试内容〗
定义、命题、逆命题、定理.定理的证明.反证法.
〖考试要求〗：
①理解证明的必要性.
②通过具体的例子，了解定义、命题、定理的含义，会区分命题的条件（题设）和结论.
③结合具体例子，了解逆命题的概念，会识别两个互逆命题，并知道原命题成立其逆命题不一定成立.
④理解反例的作用，知道利用反例可以证明一个命题是错误的.
⑤通过实例，体会反证法的含义.
⑥掌握用综合法证明的格式，体会证明的过程要求步步有据.
（2）掌握证明的依据
〖考试内容〗
一条直线截两条平行直线所得的同位角相等.
两条直线被第三条直线所截，若同位角相等，那么这两条直线平行.
若两个三角形的两边及其夹角分别相等，则这两个三角形全等.
两个三角形的两角及其夹边分别相等，则这两个三角形全等.
两个三角形的三边分别相等，则这两个三角形全等.
全等三角形的对应边、对应角分别相等.
〖考试要求〗
运用以上6条“基本事实”作为证明的依据.
（3）利用（2）中的基本事实证明下列命题
〖考试内容〗
平行线的性质定理（内错角相等、同旁内角互补）和判定定理（内错角相等或同旁内角互补，则两直线平行）.
三角形的内角和定理及推论（三角形的外角等于不相邻的两内角的和，三角形的外角大于任何一个和它不相邻的内角）.
直角三角形全等的判定定理.
角平分线性质定理及逆定理；三角形的三条角平分线交于一点（内心）.
垂直平分线性质定理及逆定理；三角形的三边的垂直平分线交干一点（外心）.
三角形中位线定理.
等腰三角形、等边三角形、直角三角形的性质和判定定理.
平行四边形、矩形、菱形、正方形、等腰梯形的性质和判定定理.
〖考试要求〗
①会利用（2）中的基本事实证明上述命题.
②会利用上述定理证明新的命题.
③练习和考试中与证明有关的题目难度，应与上述所列的命题的论证难度相当.
④通过对欧几里得《原本》的介绍，感受几何的演绎体系对数学发展和人类文明的价值.
 |
〖考点复习〗
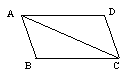
[例1]如图，已知AD∥BC，AD=CB，求证：△DAC≌△BCA.
（说明：证明过程中要求写出每步的证明依据）
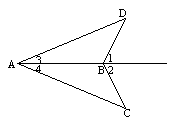
[例2]已知：如图，∠1=∠2，BD=BC.求证：∠3=∠4.
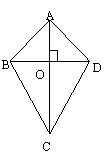
[例3]如图，四边形ABCD中，AC垂直平分BD于O，(1)图中有多少对全等的三角形？请把它们写出来。(2)任选(1)中的一对全等三角形加以证明。
 |
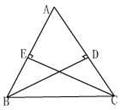[例4]如图，已知△ABC，请你增加一个条件，写出一个结论，并证明你写出的结论。
增加的条件为：
已知：
求证：
证明
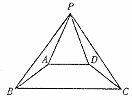[例5]如图，已知四边形ABCD是等腰梯形，AB=DC，AD∥BC，PB = PC.
求证：PA=PD.
[例6]同一底上的两底角相等的梯形是等腰梯形吗？如果是，请给出证明（要求画出图形，写出已知、求证、证明）；如果不是，请给出反例（只需画图说明）
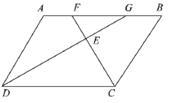[例7]如图，已知四边形ABCD是平行四边形，∠BCD的平分线CF交边AB于F，∠ADC的平分线DG交边AB于G。
（1）求证：AF=GB；
（2）请你在已知条件的基础上再添加一个条件，使得△EFG为等腰直角三角形,并
说明理由．
〖考题训练〗
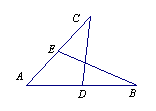
1．已知：如图，AB＝AC,AE＝AD，点D、E分别在AB、AC上．
求证：∠B＝∠C．
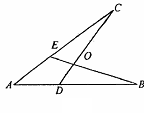2．如图.下面四个条件中，请你以其中两个为已知条件，第三个为结论，推出一个正确的命题（只需写出一种情况）.①AE = AD ②AB = AC ③OB = OC ④∠B=∠C
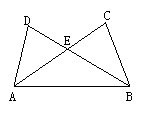
3．已知：如图，AD=BC，∠D=∠C，AC交BD于点E，求证：AC=BD.
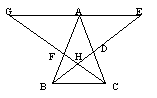
4．如图,△ABC中,AB=AC,过点A作GE∥BC,角平分线BD、CF相交于点H,它们的延长线分别交GE于点E、G.试在图中找出3对全等三角形,并对其中一对全等三角形给出证明.
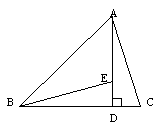5．如图，△ABC中，ÐABC＝45º，AD^BC于D，点E在AD上，且DE＝CD，求证：BE＝AC。
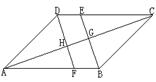
6．如图，在平行四边形ABCD中，∠B，∠D的平分线分别交对边于点E、F，交四边形的对角线AC于点G、H。求证：AH=CG。
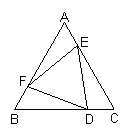
7．如图，已知△ABC为等边三角形，D、E、F分别在边BC、CA、AB上，且△DEF也是等边三角形．
（1）除已知相等的边以外，请你猜想还有哪些相等线段，并证明你的猜想是正确的；
（2）你所证明相等的线段，可以通过怎样的变化相互得到？写出变化过程．
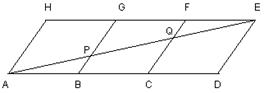
8．如图，用三个全等的菱形ABGH、BCFG、CDEF拼成平行四边形ADEH，连接AE与BG、CF分别交于P、Q，
（1） 若AB=6，求线段BP的长；（6分）
（2） 观察图形，是否有三角形与ΔACQ全等？并证明你的结论，（4分）
解：
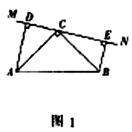
9在△ABC中，∠ACB = 90，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E.
（1）当直线MN绕点C旋转到图1的位置时，求证：①△ADC≌△CEB；②DE=AD+BE；
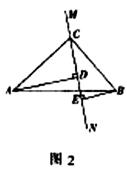
（2）当直线MN绕点C旋转到图2的位置时，求证：DE = AD-BE；
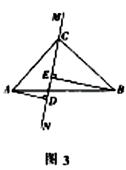
（3）当直线MN绕点C旋转到图3的位置时，试问DE、AD、BE 具有怎样的等量关系？请写出这个等量关系，并加以证明.
〖课后作业〗
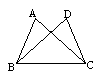
①．（2005徐州）如图，已知AB=DC，AC=DB.求证：∠A=∠D.
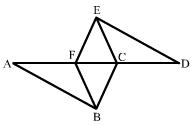②（2005安徽）如图, 已知AB∥DE, AB=DE, AF=DC, 请问图中有哪几对全等三角形? 并任选其中一对给予证明.
③．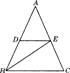
如图，在△ABC中，AB=AC，BE平分∠ABC，DE∥BC．
求证：DE=EC．
④．已知：如图，□ABCD中，BD是对角线，AE⊥BD于E，CF⊥BD于F. 求证：BE=DF.
 |
⑤．如图，在△ABC中，点D在AB上，点E在BC上，BD＝BE。
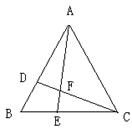（1）请你再添加一个条件，使得△BEA≌△BDC，并给出证明。
你添加的条件是：___________
证明：
（2）根据你添加的条件，再写出图中的一对全等三角形：______________（只要求写出一对全等三角形，不再添加其他线段，不再标注或使用其他字母，不必写出证明过程）
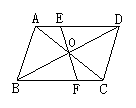
⑥．如图，四边形ABCD是平行四边形，对角线AC、BD交于点O，过点O画直线EF分别交AD、BC于点E、F。求证：OE＝OF.
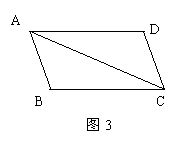
⑦．如图，将等腰直角三角形ABC的直角顶点置于直线
上，且过A、B两点分别作直线的垂线，垂足分别为D、E，请你仔细观察后，在图中找出一对全等三角形，并写出证明它们全等的过程。
