（26）图形的相似
〖考试内容〗
比例的基本性质，线段的比，成比例线段.图形的相似及性质.三角形相似的条件，图形的位似.
〖考试要求〗
①了解比例的基本性质，了解线段的比、成比例线段，通过实例了解黄金分割.
②通过实例认识图形的相似，了解相似图形的性质.知道相似多边形的对应角相等，对应边成比例，面积的比等于对应边比的平方.
③了解两个三角形相似的概念，掌握两个三角形相似的条件.
④了解图形的位似，能够利用位似将一个图形放大或缩小.
⑤通过实例了解物体的相似，利用图形的相似解决一些实际问题（如利用相似测量旗杆的高度）.
〖考点复习〗
1．比例的基本性质
[例1]．已知
，则
=＿＿＿＿＿。
2．成比例的线段
[例2]．在比例尺为1：40000的工程示意图上，将于2005年9月1日正式通车的南京地铁一号线（奥体中心至迈皋桥段）的长度约为54.3cm,它的实际长度约为（ ）
A、0.2172km B、2.172km
C、21.72km D、217.2km
3．相似图形的性质
[例3]．在△ABC中，若D、E分别是边AB、AC上的点，且DE∥BC，AD=1，DB=2，则△ADE与△ABC的面积比为____________.
4．相似三角形的判定
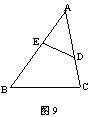
[例4]．如图9，D、E分别是△ABC的边AC、AB上的点，请你添加一个条件，使△ADE与△ABC相似．你添加的条件是
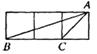
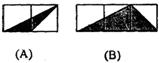
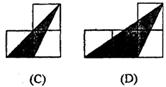
[例5]．如图，小正方形的边长均为1，则下列图中的三角形(阴影部分)与△ABC相似的是( )
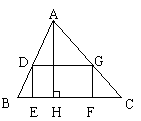
[例6]．如图，有一块三角形土地，它的底边BC=100米，高AH=80米，某单位要沿着地边BC修一座底面是矩形DEFG的大楼，D、G分别在边AB、AC上.若大楼的宽是40米，求这个矩形的面积.
〖考题训练〗
1．如果＝，那么＝＿＿＿＿＿。
3．应中共中央总书记胡锦涛同志的邀请，中国国民党主席连战先生亲民党主席宋楚瑜先生分别从台湾来大陆参观访问，先后来到西安，都参观了新建筑的“大唐芙蓉园”，该园占地面积约为80 0000ｍ2，若按比例尺1∶2000缩小后，其面积大约相当于（ ）
A. 一个篮球场的面积
B. 一张乒乓球台台面的面积
C. 《陕西日报》的一个版面的面积
D. 《数学》课本封面的面积
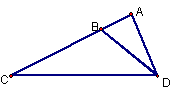
4．如图，已知△ACP∽△ABC，AC = 4，AP = 2，则AB的长为 .
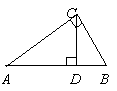5如图，已知CD是Rt△ABC的斜边上的高，其中AD=9cm，BD=4cm，那么CD等于_______cm.
6．已知：如图2，在△ABC中，∠ADE＝∠C，则下列等式成立的是（ ）
A. ＝
B. ＝
C. ＝
D. ＝
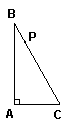
7．如图，P是Rt△ABC的斜边BC上异于B，C的一点，过P点作直线截△ABC，使截得的三角形与△ABC相似，满足这样
条件的直线共有（ ）条。
A、1 B、2 C、3 D、4
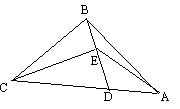
8．如图,△ABC中，D为AC上一点，CD＝2DA,∠BAC=45°,
∠BDC=60°,CE
BD,E为垂足,连接AE.
(1)写出图中所有相等的线段,并加以证明;
(2)图中有无相似三角形?若有,请写出一对;若没有,请说明理由;
(3)求△BEC与△BEA的面积之比.
〖课后作业〗
①．若 ，则的值是( )
A、 B、 C、 D、
③．如果两个相似三角形对应高的比是1：2，那么它们的面积比是 。
④．如图，D、E两点分别在AC、AB上，且DE与BC不平行，请填上一个你认为合适的条件： ，使得△ADE∽△ABC.
⑤．在△ABC中，点D、E分别在边AB和AC上，且DE∥BC，如果AD＝2，DB＝4，AE＝3，那么EC＝
⑥．在下列命题中，真命题是 （ ）
A、两个钝角三角形一定相似 B、两个等腰三角形一定相似
C、两个直角三角形一定相似 D、两个等边三角形一定相似
⑦．矩形ABCD中,M是BC边上且与B、C不重合的点,点P是射线AM上的点,若以A、P、D为顶点的三角形与△ABM相似,则这样的点有 个.
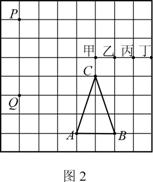
如图2，若A、B、C、P、Q、甲、乙、丙、丁都是方格纸中的格点，为使△ABC∽△PQR，则点R应是甲、乙、丙、丁四点中的
A. 甲 B. 乙 C. 丙 D. 丁
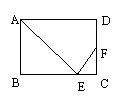
⑧．已知矩形ABCD中，AB＝2，BC＝3，F是CD的中点，一束光线从A点出发，通过BC边反射，恰好落在F点（如图），那么，反射点E与C点的距离为＿＿＿＿＿＿。
 |